- Инструменты сайта
- Основное
- Навигация
- Информация
- Действия
- Содержание
- Задача Ферма-Торричелли и ее развитие
- Обобщенная задача Ферма-Торричелли
- Плоский случай
- Механическое решение
- Геометрическое решение
- Аналитическое решение: координаты точки Ферма-Торричелли
- Аналитическое решение обобщенной задачи Ферма-Торричелли
- Аналитическое решение: исключение переменных
- Общий случай
- Существование и единственность решения
- Численное решение
- Обратная задача
- Смежные задачи
- Дерево Штейнера
- Мультифокусные эллипсы
- Треугольно-оптимизационные задачи
- Стационарные точки семейства потенциалов
- Задачи
- Источники
- Исследовательская работа по математике «Точка Ферма»
- Выберите документ из архива для просмотра:
- Описание презентации по отдельным слайдам:
- Некоторые малоизвестные факты из геометрии треугольника
- 📽️ Видео
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Благодарю Б.З.Тайбина за обнаружение 03.06.10 ошибки на настоящей странице и информирование о ней.
Видео:Задача, которую исключили из экзамена в АмерикеСкачать

Задача Ферма-Торричелли и ее развитие
Видео:Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать

Обобщенная задача Ферма-Торричелли
Задача. Пусть заданы координаты $ K_ $ точек пространства $ mathbb R^_ $ : $ <P_j=(x_,dots,x_)>_^K $. Определить координаты точки $ P_=(x_,dots,x_) $, решающей задачу оптимизации: $$ min_ F(P) qquad npu qquad F(P)= sum_^Km_j |PP_j| . $$ Здесь $ | cdot | $ означает евклидово расстояние: $ |P_1P_2|=sqrt<(x_-x_)^2+dots+(x_-x_)^2> $, а величины $ _^K $ обычно (и практически везде в настоящем разделе) считаются положительными и называются весами.
Будем говорить о наборе $$ left< begin P_1 & dots & P_K \ m_1 & dots & m_K end right> $$ как о конфигурации весов.
Видео:Шаталов за одну минуту доказывает теорему, на которую традиционно выделяется 45 минут урока!Скачать

Плоский случай
Рассмотрим сначала плоский вариант задачи: пусть $ n=2_ $, $ <P_j=(x_,y_j)>_^K $, $$ F(x,y)= sum_^ m_j sqrt . $$
Пример. В городах $ P_,P_2,P_3 $ расположены источники полезных ископаемых: железной руды, угля и воды соответственно. Известно, что для производства одной тонны стали необходимо иметь $ m_ $ тонн руды, $ m_2 $ тонн угля и $ m_3 $ тонн воды. В предположении, что стоимость перевозки одной тонны груза не зависит от его природы, где следует расположить сталелитейное производство так, чтобы минимизировать транспортные издержки?
С конца XIX века подобные задачи стали предметом изучения в экономической географии. Систематические исследования были начаты Вильгельмом Лаунхардтом 2) [6] и позднее развиты Альфредом Вебером 3) [1] . Последний ввел понятие штандорта 4) — оптимального места размещения производства, «склада».
В XX веке эти задачи выделились в подраздел теории исследования операций, известный в настоящее время как facility location problem или location theory (location analysis).
Частный случай задачи при $ n=2 , K=3 $ и $ m_1=m_2=m_3=1 $ известен как (классическая) задача Ферма-Торричелли: для трех неколлинеарных точек плоскости $ P_1=(x_1,y_1), P_2= (x_2,y_2) $ и $ P_3= (x_3,y_3) $ требуется определить $$ min_ F(x,y) quad npu quad F(x,y)= sum_^3 sqrt . $$
Datis tribus punctis, quartum reperire, a quo si ducantur tres rectæ ad data puncta, summa trium harum rectarum sit minima quantitas
(лат. Для трех заданных точек найти четвертую, такую что если от нее провести прямые линии до данных точек, сумма расстояний будет наименьшей) P. de Fermat, «Œuvres de Fermat», 1679, Livre I, Paris.
Рассмотрим теперь различные подходы к решению общей задачи. Для определения координат стационарной точки $ P_=(x_,y_) $ составим градиентную систему уравнений: $$ left< begin displaystyle frac &= displaystyle frac<sqrt<(x-x_1)^+(y-y_1)^2>>+dots+ frac<sqrt> & = 0 \ displaystyle frac &= displaystyle frac<sqrt>+dots+ frac<sqrt> & = 0 end right. $$ Система эта нелинейная и даже неалгебраическая относительно $ x_ $ и $ y_ $, поэтому уже проблема установления существования (и количества) ее вещественных решений решается специально разработанными под нее методами.
Механическое решение
Если обозначить $$ frac<sqrt<(x-x_j)^+(y-y_j)^2>> = cos gamma_j, frac<sqrt<(x-x_j)^+(y-y_1)^2>> = sin gamma_j , $$ где $ gamma_j $ означает угол, образованный вектором $ overrightarrow<PP_> $ с осью абсцисс, то уравнения градиентной системы можно переписать в виде: $$ left< begin m_1cos gamma_1 + m_2 cos gamma_2 + dots + m_Kcos gamma_K &=0,\ m_1sin gamma_1 + m_2 sin gamma_2 + dots + m_K sin gamma_K &=0 . end right. $$ Если под $ m_ $ понимать величину силы, приложенной в точке $ P_ $, и направленной к $ P_ $, то приведенные уравнения означают, что суммы проекций этих сил на координатные оси равны нулю, т.е. в точке $ P_ $ силы должны уравновешиваться. Это обстоятельство используют для экспериментального определения точки $ P_ $. На плоской доске, располагаемой горизонтально к поверхности Земли, рисуют многоугольник, подобный многоугольнику $ P_1 P_2 ldots P_K $ и просверливают в его вершинах отверстия, через которые опускают нити, связанные одним узлом. Если к свободным концам этих нитей подвесить грузы массами, пропорциональными $ m_ $, то при равновесии этой системы общий узел нитей будет находиться в искомой точке $ P_ $.
Интуитивно понятно также, что если вес $ m_ $, приложенный сквозь отверстие $ P_ $, окажется много большим оставшихся весов, то узел затянется именно в это отверстие. Оказывается при возрастании $ m_ $ такое затягивание произойдет раньше выполнения условия $ m_i = displaystyle sum_ m_j $. См. ☟ НИЖЕ.
Геометрическое решение
Известно для случая $ K=3 $ точек на плоскости для произвольных значений весов $ $ и для случая $ K=4 $ точек в случае одинаковых весов.
Исторически самое первое из известных решений задачи было предложено Торричелли в период до 1640 г. 5) . для случая $ K=3 $ точек и одинаковых весов $ m_1=m_2=m_3=1 $ (классическая задача Ферма-Торричелли). Алгоритм предлагал нахождение точки $ P_ $ в идеологии классической геометрии: circinus et regula 6) . На сторонах треугольника $ P_1P_2P_ $, как на основаниях, строятся новые треугольники — равносторонние; эти треугольники должны располагаться с внешней стороны треугольника $ P_1P_2P_ $. Для каждого треугольника строится описывающая его окружность. Пересечение этих трех окружностей и дает точку $ P_ $. На рисунке показано нахождение точки $ P_ $ для случая $ P_1=(1,1),P_2=(3,5),P_3=(7,2) $. С той поры было придумано много вариантов построения точки $ P_ $. Так, к примеру, в этой же точке $ P_ $ пересекаются прямые $ T_1 P_2 $ и $ T_2 P_1 $, и, вдобавок, $$ |T_1P_2|=|T_2P_1|=|P_ P_1|+|P_ P_2|+|P_ P_3| = min_ sum_^3 |PP_j| . $$
Это решение обобщается в [2,6] на случай различных весов. Рассмотрим систему уравнений из предыдущего пункта: $$ left< begin m_1cos gamma_1 + m_2 cos gamma_2 + m_3cos gamma_3 &=0,\ m_1sin gamma_1 + m_2 sin gamma_2 + m_3 sin gamma_3&=0 . end right. $$ Из этих уравнений выразим $ cos gamma_1 $ и $ sin gamma_1 $ и подставим в равенство $$ 1=cos^2 gamma_1+ sin^2 gamma_1 = $$ $$ =left(frac cos gamma_2 + frac cos gamma_3 right)^2+left(frac sin gamma_2 + frac sin gamma_3 right)^2 = $$ $$ = frac+ frac + 2, frac cos (gamma_2-gamma_3) . $$ Обратим внимание, что естественным ограничением на условие задачи оказывается $ |cos (gamma_2 -gamma_3)| le 1 $, что равносильно $ m_1le m_2+m_ $ (сумма двух весов должна быть не меньше третьего; на самом деле условие того, что искомая точка $ P_ $ будет отличаться от вершин $ P_1,P_2,P_3 $ более жесткое — см. ☟ НИЖЕ). Далее, из последнего равенства следует: $$ Rightarrow sin^2 (gamma_2 -gamma_3) =frac . $$ Аналогичные равенства справедливы и для синусов оставшихся пар углов. 
В случае $ m_1=m_2=m_3=1 $ последнее равенство характеризует точку треугольника, которая известна под названием точки Ферма-Торричелли: это такая точка, из которой все его вершины «видны» под углом $ 2, pi/3 $. Точка Ферма-Торричелли не всегда существует — она имеется только у треугольников, углы которых не превосходят той же величины $ 2, pi/3 $.
Теорема [3,4]. Точка Ферма-Торричелли существует только для треугольника $ P_P_2P_3 $, у которого величина каждого угла меньше $ 2pi/3 $. В этом случае она единственна и в ней достигается
$$ min_ (|PP_1|+|PP_2|+|PP_3|) , . $$ Если величина одного из углов треугольника $ ge 2pi/3 $, то минимум достигается при помещении точки $ P_ $ в эту вершину.
Пример. Для точек $ P_1=(1,1), P_2=(3,5), P_3= (7,2) $ точка Ферма-Торричелли изображена на рисунке
Ее точные координаты приведены ☟ НИЖЕ . ♦
Вернемся к рассмотрению общего случая неравных весов. На стороне $ P_P_3 $ треугольника $ P_P_2P_3 $ строится треугольник $ P_2P_3Q $, в котором 
Утверждается, что прямая $ QP_1 $ пересекает окружность, описанную вокруг треугольника $ P_2P_3Q $ в искомой точке $ P_ $. В самом деле (см. рисунок ниже), по теореме синусов для треугольника $ P_2P_3Q $ будет выполнено: $$ frac =frac =frac quad iff quad frac=frac=frac . $$ По построению точки $ P_ $ будут иметь место соотношения: $$ mu_1+nu_1=mu_2+nu_2= mu_3+nu_3= pi , $$ и, следовательно, ограничения на углы $ mu_1, mu_2, mu_3 $ оказываются такими же, как и на $ |gamma_3-gamma_2 |, |gamma_3-gamma_1 |, |gamma_2-gamma_1 | $.
Длина отрезка $ |P_1Q| $ позволяет определить величину минимального значения функции: $$ m_1 |P_1Q| = m_1 |P_ P_1|+m_2 |P_ P_2|+ m_3 |P_ P_3| = min_ sum_^3 m_j|PP_j| . $$ В предыдущих рассуждениях предполагается, что точка $ P_ $ лежит внутри треугольника $ P_P_2P_3 $. В противном случае, решением задачи будет одна из вершин треугольника.
Пример. Найти точку $ P_ $ для конфигурации
Решение. Здесь $ |P_2P_3|=4 $, следовательно $ |P_2Q|=4 cdot 2 = 8, |P_3Q|=4 cdot 3/2 = 6 $. Этими условиями определяем точку $ Q_ $ — как одну из двух точек пересечения окружностей (радиуса $ 8_ $ с центром в точке $ P_ $ и радиуса $ 6_ $ с центром в $ P_3 $).
Её координаты: $ approx (6.5,-4.8) $. Проводим окружность через точки $ P_2,P_3,Q $. Прямая $ QP_1 $ пересекает ее в искомой точке $ P_ approx (3.9, 1.4) $ при минимальном значении для минимизируемой функции: $ F(x_,y_) approx 23.4 $.
Точные значения приведены ☟ НИЖЕ. ♦
Для $ K=4 $ точек на плоскости геометрическое решение известно только для случая одинаковых весов.
Теорема [Фаньяно]. Если точки $ P_,P_2,P_3, P_ $ образуют выпуклый четырехугольник, то
$$ min_ left(|PP_1|+|PP_2|+|PP_3|+|PP_| right)$$ достигается в точке $ P_ $, лежащей на пересечении диагоналей четырехугольника: $$ x_=frac, $$ $$ y_=frac , . $$ Если же точки $ P_,P_2,P_3, P_ $ не образуют выпуклый четырехугольник, и точка $ P_ $ лежит внутри треугольника, образованного тремя оставшимися точками, то минимум суммы расстояний достигается в точке $ P_ $.
Аналитическое решение: координаты точки Ферма-Торричелли
Теорема.[11] Пусть все углы треугольника $ P_P_2P_3 $ меньше $ 2pi /3 $, или, что то же, выполнены условия:
Если выписать символьные представления для $ x_ $ и $ y_ $ в виде функций от параметров $ _^3 $, то можно осуществить сокращение на общий множитель $ |S| $ числителей и знаменателей получившихся в теореме дробей ☟
Теорема.[5,11] Пусть все углы треугольника $ P_P_2P_3 $ меньше $ 2pi /3 $. Точка $ P_ $ Ферма-Торричелли имеет координаты
$$ x_=frac<2sqrtd>, y_= frac<2sqrtd> $$ при $$ |P_1P_|+|P_2P_|+|P_3P_|= sqrt . $$ Здесь $$ d=frac<r_^2+r_^2+r_^2>+sqrt cdot | S | ; $$ $$ X=sqrt [x_1r_^2+x_2r_^2+x_3r_^2] +(x_1+x_2+x_3) cdot |S|+ $$ $$ +3 operatorname (S) [(y_2-y_1)(x_1x_2+y_1y_2)+(y_1-y_3)(x_1x_3+y_1y_3)+(y_3-y_2)(x_2x_3+y_2y_3)]; $$ $$ Y=sqrt [y_1r_^2+y_2r_^2+y_3r_^2]+ (y_1+y_2+y_3) cdot |S| — $$ $$ -3 operatorname (S)[(x_2-x_1)(x_1x_2+y_1y_2)+(x_1-x_3)(x_1x_3+y_1y_3)+(x_3-x_2)(x_2x_3+y_2y_3)] ; $$ $$ S=x_1y_2+x_2y_3+x_3y_1-x_1y_3-x_3y_2-x_2y_1= $$ $$ =left|begin x_2-x_1 & x_3-x_1 \ y_2-y_1 & y_3-y_1 end right|= left| begin 1 & 1 & 1 \ x_1 & x_2 & x_3 \ y_1 & y_2 & y_3 end right| . $$
Пример. При $ P_1=(1,1),P_2=(3,5),P_3=(7,2) $ будет:
$$ x_=frac left( 1029 + 79 sqrtright) approx 3.3939,qquad y_=frac left( 1053 + 647 sqrt right) approx 3.1639 , $$ $$ |P_P_1|+|P_P_2|+|P_P_3| = sqrt<41+22sqrt>approx 8.8941 . $$ При $ P_1=(1,2),P_2=(3,3),P_3=(4,1) $ : $$ x_=frac(15+sqrt) approx 2.7886,qquad y_=frac(3+sqrt) approx 2.3660 ; $$ $$ |P_P_1|+|P_P_2|+|P_P_3| = sqrt<5,(2+sqrt)>approx 4.3197 , . $$
Аналитическое решение обобщенной задачи Ферма-Торричелли
Получено только для случая $ K=3 $.
Теорема.[11] Обозначим величину угла треугольника $ P_P_2P_3 $ при вершине $ P_ $ через $ alpha_j $. Если нарушено $ j $-е из трех условий
Пример. Для конфигурации
$$ left<begin P_=(2,6) & P_=(1,1) & P_=(5,1) \ m_=2 & m_=3 & m_=4 end right> $$ точка $ P_ $ имеет координаты $$ x_=frac<4103+1833 sqrt>approx 3.9086 , y_ =frac<29523-4481 sqrt>approx 1.4152 , . $$ Минимальное значение для функции: $$ min F(x,y)= m_1|P_P_1|+m_2|P_P_2|+m_3|P_P_3|= 2sqrt<79+15sqrt> approx 23.4174 , . $$ ♦
Аналитическое решение: исключение переменных
В случае $ K>3 $ точек аналитическое решение для обобщенной задачи Ферма-Торричелли вряд ли может быть получено. Тем не менее, можно попытаться продвинуться аналитикой возможно дальше, именно: свести поиск координаты точки $ P_ $ к решению системы полиномиальных (алгебраических) уравнений и попытаться применить к этой системе методы исключения переменных.
Пример. Выяснить динамику поведения точки $ P_ $ для конфигурации
$$ left< begin P_=(1,1) & P_=(3,5) & P_=(7,2) & P_=(6,6) \ m_=1 & m_=1 & m_=1 & m_=m end right> $$ в зависимости от изменения параметра $ m_ $.
Решение. При каждом конкретном значении параметра $ m_ $ координаты стационарной точки $ P_ $ можно найти применением численных методов, но нас интересует хоть какое-то функциональное представление для $ P_ (m) $.
Дальнейшее упрощение вряд ли возможно: уравнения неприводимы над $ mathbb Q_ $, и, скорее всего, неразрешимы в радикалах.
Можно пойти другим путем: исключать параметр $ m_ $ с целью нахождения неявного представления кривой, на которой расположены стационарные точки при всех возможных значениях $ m_ $. Результант $ mathcal R_m(F_1,F_2) $ оказывается полиномом степени $ 96 $ по $ x_ $ и $ y_ $, и этот полином факторизуется в виде $$ 65536 (2x-y-1)^8(x^2-14x+53-4y+y^2)^8(x^2-12,x+72-12y+y^2)^8 Phi_0^2(x,y) Phi^2(x,y) . $$ Собственно кривая стационарных точек задается одним множителем: $$ Phi(x,y) = 0 $$ при $$ Phi(x,y) =3,y(-7,y+10,x)(8,x-y)(2,x-9,y)(x^2+y^2)^4+ $$ $$ +8,(160,x^5-2594,x^4y+10117,x^3y^2+3152,x^2y^3-6209,xy^4+183,y^5)(x^2+y^2)^3- $$ $$ -4,(10144,x^6-106368,x^5y+344359,x^4y^2+303368,x^3y^3+32554,x^2y^4-193808,xy^5-16853,y^6)(x^2+y^2)^2 $$ $$ +dots -1152, (2823793,x^2-22813720,xy-56866,y^2)+4409856 (1491,x+1234,y)-2110116096 . $$ Полное выражение для функции $ Phi $ и картина всей кривой $ Phi=0 $ целиком достаточно сложны: см. ☞ ЗДЕСЬ. На рисунке выделена только ветвь, которая соответствует реальной динамике стационарной точки.
«Контрольные» точки на этой ветви:
x $ left(frac(1029 + 79sqrt),frac(1053 + 647sqrt) right) $ — точка Ферма-Торричелли треугольника $ P_1P_2P_ $, соответствует значению $ m=0 $;
x $ left(frac,fracright) $ — точка пересечения диагоналей четырехугольника $ P_1P_2P_3P_4 $, соответствует значению $ m_=1 $ (см. ☞ теорему Фаньяно);
♦ $ (6,6) $ — вершина $ P_ $, соответствует значению $ m approx 2.4436 $ (точное значение ☞ ЗДЕСЬ);
♦ $ (1,1) $ — вершина $ P_ $, соответствует значению $ m approx -2.4184 $ (вообще говоря, в постановке задачи говорится только о положительных значениях весов, но почему бы не осуществить аналитическое продолжение? );
x $ (frac,frac) $, соответствует $ m=1-sqrt approx 0.3675 $.
Видео:Метод вырезания узлов. Определение усилий в ферме. СопроматСкачать

Общий случай
Обращаемся к задаче в $ mathbb R^_ $. Стационарные точки функции $$ F(P)=sum_^Km_j |PP_j| $$ являются решениями градиентной системы уравнений $$ frac=0,dots, frac=0 , $$ которую можно записать в векторном виде $$ sum_^K m_jfrac = mathbb O_ . $$ При этом следует иметь в виду, что, во-первых, при некоторых конфигурациях система может оказаться несовместной и, во-вторых, искомый минимум функции может достигаться в одной из точек $
$ (которые последней системой не «отлавливаются»).
Видео:Великая теорема ФермаСкачать

Существование и единственность решения
Теорема. Пусть точки $
_^K subset mathbb R^n $ все различны. Минимум функции $$ F(P)=sum_^K m_j |PP_j| $$ существует и единствен. При этом
1. если существует точка $ P_ $ такая, что выполняется условие $$ left|sum_^K m_j frac
right| le m_i , $$ то $ min F(P) $ достигается в точке $ P_ $;
2. если для любого значения $ i in $ выполняется условие $$ left|sum_^K m_j frac
right| > m_i , $$ то $ min F(P) $ достигается в точке $ P_ $, удовлетворяющей градиентной системе уравнений $$ sum_^K m_j frac=mathbb O_, ; $$ и, в этом случае, $ P_ notin
_^K $.
Доказательство ☞ ЗДЕСЬ
Пример. При каких значениях параметра $ m_ $ в конфигурации
$$ left< begin P_=(1,1) & P_=(3,5) & P_=(7,2) & P_=(6,6) \ m_=1 & m_=1 & m_=1 & m_=m end right> $$ $ min sum_^4 m_j|PP_j| $ достигается в точке $ P_4 $?
Решение. Формируем условие $$ left| m_1 frac<sqrt>+m_2frac<sqrt>+m_3 frac<sqrt> right| le m_4 . $$ Ответ. При $ m ge sqrt<3+4/sqrt+3sqrt+sqrt> approx 2.4436 $.
В случае $ n=2, K=3 $ условия теоремы переформулируются в терминах углов $ alpha_1,alpha_2, alpha_3 $ треугольника $ P_1P_2P_ $. Так, например, условие 2 эквивалентно
$$ m_2^2+m_3^2+2, m_2m_3 cos alpha_1 > m_1^2 , m_1^2+m_3^2+2, m_1m_3 cos alpha_2 > m_2^2, m_1^2+m_2^2+2, m_1m_2 cos alpha_3 > m_3^2, . $$ Если $ m_1=m_2=m_3 $, то эти условия означают, что все углы треугольника меньше $ 2pi/3 $. В общем же случае (не обязательно равных весов) этим условиям можно придать следующую геометрическую интерпретацию. Их выполнение означает, что рассматривая величины весов $ m_1,m_2,m_3 $ в качестве длин отрезков, мы можем построить из этих отрезков треугольник — он так и называется: «весовой треугольник» [1].
Обозначим углы этого треугольника $ beta_1, beta_2, beta_3 $ в соответствии с рисунком. Тогда, по теореме косинусов, получаем: $$ cos alpha_j+ cos beta_j > 0 quad npu quad jin , . $$
Видео:Построение высоты в треугольникеСкачать

Численное решение
Рассмотрим задачу в $ mathbb R^_ $ сначала для случая одинаковых весов $ m_1=dots=m_K=1 $. Перепишем градиентную систему уравнений $$ frac+dots+frac= mathbb O_, $$ задающую стационарные точки функции $ F(P) $, в эквивалентном виде $$ P=underbrace<left(frac
+dots+frac
right) bigg/ left(frac+dots+frac right)>_ , . $$ Решать последнюю систему будем методом простой итерации. Возьмем в качестве начального приближения произвольную точку $ P^ notin
_^K $ и строим последовательность по рекурсивной формуле $$ P^=Phi(P^) quad npu quad k in mathbb N . $$ Утверждается, что эта последовательность сходится к точке $ P_ $, являющейся точкой минимума функции $ F(P)=sum_^K |PP_j| $.
Метод известен как алгоритм Вайсфельда [14].
Пример. Для $ P_1=(1,1), P_2=(3,5), P_3=(7,2) $ возьмем $ P^=(2,2) $. Итерационная последовательность
$$ left(begin 2 \ 2 end right) to left(begin 2.4979 \ 2.1974 end right) to left(begin 2.8581 \ 2.4862 end right) to left(begin 3.1122 \ 2.7295 end right) to dots to P^ =left(begin 3.3_ \ 3.1_ end right) to dots $$ сходится к точке Ферма-Торричелли $ P_approx (3.3939, 3.1639 ) $. ♦
Пример. Для $ P_1=(1,1,0), P_2=(5,1,0), P_3=(2,6,0), P_4=(3,3,5) $ возьмем $ P^=(1,1,1) $. Итерационная последовательность
$$ left(begin 1 \ 1 \ 1 end right) to left(begin 1.9583 \ 1.8361 \ 0.6226 end right) to left(begin 2.3007 \ 2.1007 \ 0.7319 end right) to left(begin 2.5077 \ 2.2665 \ 0.8386 end right) to dots to P^= left(begin 2.6_ \ 2.42_ \ 0.9_ end right) to dots $$ сходится к точке $ P_ approx (2.6823, 2.4298, 0.9607) $. ♦
Проблемы сходимости возникают в случае, когда искомая точка $ P_ $ близка к одной из $
_^K $.
Пример. Для
$$ P_1=(0,0), P_2=(1,0), P_3=(-4,7) $$ координаты точки Ферма-Торричелли: $ P_approx (0.0023,0.0039) $. Итерационная последовательность, стартующая из $ P^=(0,1) $, не дает этой точности при $ 200 $ итерациях. ♦
Метод очевидным образом обобщается и на случай, когда веса в конфигурации не обязательно одинаковы: в рекурсивной формуле следует взять $$ Phi(P)=left(frac+dots+frac right) bigg/ left(frac+dots+frac right) . $$
Видео:Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

Обратная задача
Задача. Подобрать величины весов $ _^K $ так, чтобы минимум функции $ displaystyle F(P)=sum_^K m_j |PP_j| $ находился в наперед заданной точке $ P_ notin
_^K $.
В отличие от «прямой» задачи, обратная имеет довольно простое решение. Начнем рассмотрение со случая плоскости: $ n=2, K=3 $.
Теорема [11]. Пусть вершины треугольника $ P_P_2P_3 $ пронумерованы против часовой стрелки. Тогда для значений
$$ m_1^ = |P_P_1| cdot left| begin 1 & 1 & 1 \ x_ & x_2 & x_3 \ y_ & y_2 & y_3 end right|, m_2^ = |P_P_2| cdot left| begin 1 & 1 & 1 \ x_1 & x_ & x_3 \ y_1 & y_ & y_3 end right|, m_3^ = |P_P_3| cdot left| begin 1 & 1 & 1 \ x_1 & x_2 & x_ \ y_1 & y_2 & y_ end right| $$ функция $$ F(x,y) = sum_^3 m_^ sqrt $$ имеет стационарную точкой точку $ P_=(x_,y_) $. Если последняя выбирается внутри треугольника $ P_P_2P_3 $, то величины $ m_1^,m_2^,m_3^ $ все положительны и $$ F(x_,y_)=min_ F(x,y)= left| begin 1 & 1 & 1 & 1\ x_ & x_1 & x_2 & x_3 \ y_ & y_1 & y_2 & y_3 \ x_^2+y_^2 & x_1^2+y_1^2 & x_2^2+y_2^2 & x_3^2+y_3^2 end right| . $$
Доказательство теоремы, а также геометрический смысл величин из ее формулировки ☞ ЗДЕСЬ.
Пример. Поместить в точках $ P_=(2,6),P_=(1,1), P_=(5,1) $ соответствующие веса $ <m_j^> $ так, чтобы точка минимума функции $ F(x,y) $ находилась бы в точке
Решение. Формулы из теоремы дают: $$ left<begin m_1^&=& displaystyle frac<2(20925-4481sqrt)>sqrt<316380606+35999826sqrt> ,\ m_2^&=& displaystyle frac<2(15105-2342sqrt)>sqrt<75400161-9169767sqrt> , \ m_3^&=& displaystyle frac<8(-1185+15988sqrt)>sqrt<8335761-2050623sqrt> , end right. $$ при $$ F(x_,y_)=frac(-333980+193436sqrt) . $$ Сравним этот результат с полученным ☝ ВЫШЕ. В соответствии с замечанием, должно выполняться: $ m_1^ : m_2^ : m_3^ = 2 : 3 : 4 $. А проверьте! ♦
Обобщение результата в многомерный случай $ n>2 $ для числа точек $ K=n+1 $ ☞ ЗДЕСЬ.
Видео:Куда упадёт узелок с грузами или задача Ферма про точку Торричелли?Скачать

Смежные задачи
Видео:Теорема, которую скрывали 200 летСкачать
Дерево Штейнера
Задача. Пусть заданы точки $ P_1,dots,P_K $ на плоскости. Требуется построить связную систему $ mathbf L_ $ прямолинейных отрезков на той же плоскости, чтобы
1. любые две точки $ P_ $ и $ P_ $ могли быть связаны ломаной линией, звенья которой входили бы в состав системы $ mathbf L_ $;
2. общая длина всей системы $ mathbf L_ $ была наименьшей.
Такая система $ mathbf L_ $ называется минимальным деревом Штейнера, ее построение и применения см. в [3,4].
На первый взгляд кажется, что эта задача эквивалентна задаче Ферма-Торричелли в случае одинаковых весов и речь идет о поиске единственной точки $ P_ $ на плоскости. На самом деле, решение этой задачи для случая $ K ge 4 $ предполагает построение нескольких вспомогательных точек.
Пример. Построить минимальное дерево Штейнера для точек $$ P_1=(0,3), P_2=(0,0), P_3=(4,0), P_4=(4,3) , . $$
Решение. Будем пробовать варианты решения задачи, последовательно добавляя вспомогательные точки. Если не добавлять дополнительных точек вообще, то эта задача относится к классу задач построения минимального покрывающего дерева 7) . В такой постановке решением рассматриваемого примера будет ломаная $ P_1P_2P_3P_4 $ длиной $ 3+4+3=10 $.
Если разрешено добавить одну дополнительную точку, то решением задачи, в соответствии с ☝ теорему Фаньяно, будет система из двух диагоналей прямоугольника:
Тем не менее, выигрыша в длине дерева не получим: $ 5+5=10 $. Но если разрешено добавлять две дополнительных точки, то расположив их в $ P_=left(frac<sqrt>,frac right) $ и $ P_=left(4-frac<sqrt>,frac right) $
получим суммарную длину равной $ 4+ 3sqrt approx 9.196152 $.
Можно ли улучшить этот результат добавлением еще большего количества дополнительных точек? Ответ отрицателен: оказывается, что для произвольной конфигурации системы $
_^4 $ количество дополнительных точек, необходимых для решения задачи о минимальном дереве, никогда не превысит двух. ♦
В рассмотренном примере точка $ P_ $ является точкой Ферма-Торричелли для треугольника $ P_1 P_2 P_ $, а точка $ P_ $ — точкой Ферма-Торричелли для треугольника $ P_3 P_4 P_ $. Это свойство оказывается принципиальным для решения общей задачи: для любой конфигурации точек $
_^K subset mathbb R^2 $ минимальное дерево Штейнера является графом, соединяющим эти точки с дополнительными узлами графа, составляющими некоторое множество $ < S_>_^M $. Мощность этого дополнительного множества находится в пределах $$ 0 le M le K-2 , ,$$ и, при условии, что оно не пусто, любой его элемент является точкой Ферма-Торричелли для некоторой тройки точек из объединения $
_^K bigcup < S_>_^M $. Степень каждой вершины $
_^K $ графа равна либо $ 1_ $ либо $ 2_ $.
Задача о минимальном дереве Штейнера обсуждается ☞ ЗДЕСЬ.
Видео:Математика это не ИсламСкачать

Мультифокусные эллипсы
Для случая $ n=2_ $ рассмотрим задачу о линиях уровня функции $$ F(x,y)= sum_^ sqrt , $$ т.е. о кривых $ F(x,y)=c $ при различных значениях $ c_ $. В случае $ K=2 $ решение задачи хорошо известно — это либо эллипс с фокусами в точках $ P_1=(x_1,y_1),P_2=(x_2,y_2) $, либо отрезок, соединяющий эти точки, либо пустое множество (мнимый эллипс). Что за кривые соответствуют случаям $ K ge 3 $? Например, каково геометрическое место точек, сумма расстояний от которых до фиксированных точек $ P_1,P_2,P_3 $ будет постоянной величиной? Этот вопрос был задан Декартом Ферма в 1638 г. (и именно отсюда возникла у Ферма постановка задачи о поиске минимума функции $ F_ $).
Эти кривые называются мультифокусными (мультифокальными) эллипсами,полиэллипсами или обобщенными эллипсами. В немецком языке известны также под названием Tschirnhaus’sche Eikurve — яйцеобразные кривые Чирнгауза 8) . Они могут считаться алгебраическими кривыми — последовательным возведением их уравнений в квадрат можно избавиться от радикалов.
Пример. Для $ P_1=(1,1),P_2=(3,5),P_3=(7,2) $ семейство трехфокусных эллипсов (алгебраических кривых порядка $ 8_ $) выглядит так (числа на кривых — значения константы $ c_ $):
Каким значениям $ c_ $ соответствуют кривые, проходящие через точки $ P_1, P_2, P_3 $ ? ♦
В случае когда веса $ $ могут быть различными, линии уровня функции $$ F(x,y)= sum_^ m_jsqrt , $$ не имеют установившегося названия. В случае $ K=2 $ в литературе встречаются под названием овалы Декарта; сам Декарт называл их эллипсами второго рода. Если $ Kge 3 $ и величины весов $ $ рационально соизмеримы, то этот случай может быть быть рассмотрен как предельный случай мультифокусного эллипса — когда некоторые из фокусов сливаются в один. Этими кривыми в середине XIX века интересовался (из любознательности) один шотландский ученый [7]. В случае $ K=3 $ кривые известны в экономической географии под названием изодапан 9) ; каждая такая кривая состоит из точек одинаковой суммарной стоимости транспортных перевозок до них из $
$.
Анимация трехмерного аналога мультифокусного эллипса ☞ ЗДЕСЬ (470 Kb).
Видео:По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Треугольно-оптимизационные задачи
Задача 1. Построить максимальный равносторонний треугольник $ Q_1Q_2Q_3 $, описанный вокруг заданного треугольника $ P_P_P_3 $ (на каждой стороне треугольника $ Q_Q_Q_3 $ должна лежать одна вершина треугольника $ P_1P_2P_3 $).
Теорема. Пусть все углы треугольника $ P_P_P_3 $ меньше $ 2pi/3 $. Высота искомого треугольника $ Q_1Q_2Q_3 $ равна $ |P_P_1|+|P_P_2|+|P_P_3| $, где $ P_ $ — точка Ферма-Торричелли треугольника $ P_P_P_3 $. Стороны треугольника $ Q_1Q_2Q_3 $ перпендикулярны прямым $ P_P_1, P_P_2 $ и $ P_P_3 $.
Задача 2. Построить минимальный равносторонний треугольник $ R_1R_2R_3 $, вписанный в заданный треугольник $ P_P_P_3 $ (на каждой стороне треугольника $ P_P_P_3 $ должна лежать одна вершина треугольника $ R_1R_2R_3 $).
На удивление, ссылок в интернете на решение задачи 2 я не нашел, за исключением ☞ ЭТОЙ. Задача похожа на задачу Фаньяно о построении произвольного треугольника минимального периметра, вписанного в данный остроугольный [4]; однако требование равносторонности треугольника в условии задачи существенно меняет ее решение.
Теорема. Пусть все углы треугольника $ P_P_P_3 $ меньше $ 2pi/3 $. Стороны искомого треугольника $ R_1R_2R_3 $ параллельны сторонам треугольника $ Q_1Q_2Q_3 $, решающего предыдущую задачу. Имеет место соотношение между площадями трех треугольников — исходного, максимального описанного и минимального вписанного: $$ frac< S_>< S_>=frac< S_><S_> . $$
Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Стационарные точки семейства потенциалов
Задача. Найти стационарные точки функции $$ F(P)= sum_^K m_j left|PP_j right|^L . $$ Здесь $
subset mathbb R^n $, $ L_ $ предполагается вещественным ненулевым числом, а величины $ < m_>_^K $ — произвольными вещественными числами (не обязательно положительными).
В случае $ L=1 $ мы получаем обобщенную задачу Ферма-Торричелли, рассмотренную выше. В случае $ L=2 $ решением задачи является единственная точка $$ P_= frac<sum_^K m_jP_j>< sum_^K m_j> $$ — точка глобального минимума функции $ F(P) $. В случае всех положительных $ _^K $ и $ nin $ точка $ P_ $ является центром масс (барицентром) системы материальных точек, расположенных в точках $
_^K $.
Нас интересует решение задачи для других показателей $ L_ $. Поставленной задаче можно придать физический смысл. Пусть в пространстве имеется конфигурация $$ left<begin P_1 & dots & P_K \ m_1 & dots & m_K end right> $$ из $ K_ $ фиксированных (неподвижных) точечных заряженных частиц, которые воздействуют на пробный точечный единичный заряд величины, помещенный в точку $ P_ $; при этом сила воздействия $ j_ $-го заряда прямо пропорциональна величине заряда $ m_ $ и пропорциональна некоторой степени $ L_ $ расстояния от этого заряда до пробного. Требуется найти точку $ P_ in mathbb R^_ $, при помещении в которую пробного заряда, последний будет неподвижен (находиться в положении равновесия).
Особый интерес представляет частный случай поставленной задачи: $ L=-1 $. Этому случаю соответствует два физических потенциала — кулоновский (электростатический) и ньютоновский (гравитационный) 10) .
Стационарные точки этого семейства потенциалов задаются градиентной системой уравнений $$ left<frac<partial x_>= L sum_^ m_j |PP_j|^ frac<(x_-x_)> = 0 right>_^n , quad npu quad begin <P_j=(x_,dots,x_)>_^K, \ P=(x_1,dots,x_n) end , $$ которая при четных значениях $ L_ $ является алгебраической (или может быть немедленно приведена к алгебраической в случае отрицательных $ L_ $); в остальных же случаях она будет содержать радикалы, от которых можно избавиться только последовательным возведением уравнений в квадрат. Уже для случая кулоновского потенциала $ L=-1, n=2, K=3 $ это приводит к алгебраическим уравнениям высокой степени с громоздкими коэффициентами.
Пример. Пусть $ P_1=(1,1), P_2=(5,1) , P_3=(2,6) $. Проанализировать поведение множества стационарных точек функции
Решение. Градиентная система уравнений $$ begin displaystyle frac<sqrt^3>& displaystyle +frac<sqrt^3>& displaystyle +frac<sqrt^3>=0, , \ displaystyle frac<sqrt^3>& displaystyle +frac<sqrt^3>& displaystyle +frac<sqrt^3>=0 , end $$ может быть преобразована в алгебраическую в ходе следующей процедуры. Обозначим $ A_1, A_2 $ и $ A_3 $ слагаемые в любом из этих уравнений. Последовательное возведение в степень по схеме $$ A_1+A_2+A_3=0 quad Rightarrow quad (A_1+A_2)^2=A_3^2 quad Rightarrow quad (2, A_1A_2)^2 = (A_3^2-A_1^2 — A_2^2)^2 $$ приводит систему к алгебраической $$ F_1(x,y,m_2,m_3)=0, F_2(x,y,m_2,m_3)=0 . $$ Здесь $ F_ $ и $ F_ $ — полиномы степени $ 28 $ по переменным $ x_ $ и $ y_ $ с коэффициентами порядков до $ 10^ $. Нахождение всех решений этой системы — даже для конкретных (фиксированных) значений параметров $ m_2 $ и $ m_3 $ — становится вычислительно сложной задачей. А ведь требуется решить еще более сложную задачу: проследить динамику этого множества при изменении параметров!
Сложность поставленной задачи — по сравнению с обобщенной задачей Ферма-Торичелли — заключается еще и в том, что что число вещественных решений системы больше единицы; в зависимости от значений параметров, число стационарных точек — от $ 2_ $ до $ 4_ $. ♦
Гипотеза [Максвелл] [8,15]. Число стационарных точек кулоновского поля любой конфигурации $ K_ $ стационарных зарядов в $ mathbb R^3 $ не превосходит $ (K-1)^2 $. Не доказана 11) .
Что общего у поставленной в начале пункта задачи с обобщенной задачей Ферма-Торричелли? — То, что похожим образом решается обратная задача. Рассмотрим сначала плоский случай.
Теорема [12, 13]. Пусть точки $ P_=(x_1,y_1),P_2=(x_2,y_2),P_3=(x_3,y_3) $ неколлинеарны. Тогда для значений
$$ m_1^ = |P_P_1|^ left| begin 1 & 1 & 1 \ x_ & x_2 & x_3 \ y_ & y_2 & y_3 end right|, m_2^ = |P_P_2|^ left| begin 1 & 1 & 1 \ x_1 & x_ & x_3 \ y_1 & y_ & y_3 end right|, m_3^ = |P_P_3|^ left| begin 1 & 1 & 1 \ x_1 & x_2 & x_ \ y_1 & y_2 & y_ end right| $$ функция $$ F(x,y) = sum_^3 m_^ |PP_j|^L $$ имеет стационарную точку $ P_=(x_,y_) $. При этом $$ F(x_,y_)= left| begin 1 & 1 & 1 & 1\ x_ & x_1 & x_2 & x_3 \ y_ & y_1 & y_2 & y_3 \ x_^2+y_^2 & x_1^2+y_1^2 & x_2^2+y_2^2 & x_3^2+y_3^2 end right| . $$
Доказательство фактически повторяет приведенное ☞ ЗДЕСЬ.
Результат предыдущей теоремы позволяет существенно упростить решение «прямой» задачи.
Теорема [12, 13].Обозначим
$$ S_1(x,y)= left| begin 1 & 1 & 1 \ x & x_2 & x_3 \ y & y_2 & y_3 end right|, S_2(x,y)= left| begin 1 & 1 & 1 \ x_1 & x & x_3 \ y_1 & y & y_3 end right|, S_3(x,y)= left| begin 1 & 1 & 1 \ x_1 & x_2 & x \ y_1 & y_2 & y end right| , . $$ Любое решение системы $$ partial F / partial x = 0, partial F / partial y = 0 , $$ отличное от $
$, удовлетворяет соотношению $$ m_1:m_2:m_3=|PP_1|^ S_1(x,y):|PP_2|^ S_2(x,y):|PP_3|^ S_3(x,y) . $$ В случае, когда $ L_ $ четно, вторая система ни чем не лучше первой: степени получающихся алгебраических уравнений одинаковы. Но вот в случае, когда $ L_ $ — нечетно (как в случае кулоновского потенциала), преимущество второй системы становится очевидным: избавиться от радикалов можно однократным возведением в квадрат.
Для нечетных значений $ Lin mathbb Z $ стационарные точки функции $ F_ $ удовлетворяют системе алгебраических уравнений
Пример. В рассмотренном выше примере функции
$$ F(x,y)=frac<sqrt>+ frac<sqrt>+frac<sqrt> $$ предложенный алгоритм приводит к системе $$ widetilde F_1(x,y,m_2,m_3)=0, widetilde F_2(x,y,m_2,m_3)=0 , $$ при $$ begin widetilde F_1(x,y,m_2,m_3)= \ =m_2^2,(5,x+3,y-28)^2(x^2+y^2-2,x-2,y+2)^3 -(5,x-y-4)^2(x^2+y^2-10,x-2,y+26)^3 , \ widetilde F_2(x,y,m_2,m_3)= \ =m_2^2,(4,y-4)^2(x^2+y^2-4,x-12,y+40)^3 -m_3^2,(5,x-y-4)^2(x^2+y^2-10,x-2,y+26)^3. end $$ Здесь $ deg widetilde F_1 = deg widetilde F_2 =8 $ относительно переменных $ x_ $ и $ y_ $; это можно считать существенным успехом в сравнении с $ 28 $-й степенью уравнений, полученных в ходе первоначального решения.
Допустим, мы хотим исследовать динамику множества вещественных решений этой системы при различных фиксированных значениях $ m_2 $ и для произвольных значений $ m_3 $. Для получения неявного задания кривой $$ H(x,y,m_2) = 0 , $$ которая будет состоять из решений системы при всевозможных значениях $ m_3 $, мы должны исключить этот параметр из системы. Но он, фактически, уже исключен: первое уравнение от него не зависит! Иными словами, утверждается, что уравнение $$ m_2^2,(5,x+3,y-28)^2(x^2+y^2-2,x-2,y+2)^3 -(5,x-y-4)^2(x^2+y^2-10,x-2,y+26)^3=0 $$ при каждом фиксированном значении $ m_=m_ $ определяет на плоскости $ (x,y) $ кривую, целиком состоящую из стационарных точек семейства кулоновских потенциалов $$ left< frac<sqrt>+ frac<m_><sqrt>+frac<sqrt> right>_ . $$ Изобразим несколько таких кривых на рисунке (числа на кривых обозначают величины $ m_2 $; ветви одинакового цвета соответствуют одинаковым значениям этого заряда).
Более подробное исследование этой задачи ☞ ЗДЕСЬ.
Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Задачи
Видео:Великая теорема Ферма для n=3 (первая лекция)Скачать

Источники
При составлении настоящего раздела существенно использовалось содержание обзорной статьи
[*] . Martini H. Fermat-Torricelli problem. Encyclopedia of Mathematics. Supplement III. Kluwer Academic Publishers. 2001, C.149-151
[1]. Weber A. Über den Standort der Industrien. Teil I: Reine Theorie des Standorts. J.C.B.Mohr, 1909. Tübingen.
Вебер А. Теория размещения промышленности. М.-Л. «Книга». 1926. (На самом деле, последняя книга — не перевод оригинальной книги Вебера, а изложение ее содержания переводчиком Н.Морозовым 12) ).
[3]. Курант Р., Роббинс Г. Что такое математика? М.МЦНМО. 2004
[4]. Протасов В.Ю. Максимумы и минимумы в геометрии. М.МЦНМО. 2005
[5]. Уланов Е.А., Утешев А.Ю. Аналитическое решение обобщенной задачи Ферма-Торричелли-Штейнера./ / Процессы управления и устойчивость: Труды 42-й международной научной конференции аспирантов и студентов / Под ред. А. С. Ерёмина, Н. В. Смирнова. СПб.: Издат. Дом С.-Петерб. гос. ун-та, 2011. С. 201–206.
[6]. Launhardt W. Kommercielle Tracirung der Verkehrswege. Zeitschrift f. Architekten u.Ingenieur-Vereinis im Königreich Hannover. V. 18, pp. 516-534, 1872. Текст ☞ ЗДЕСЬ.
[7]. Maxwell J.C. Paper on the Description of Oval Curves. Observations on Circumscribed Figures Having a Plurality of Foci, and Radii of Various Proportions. 1846. «The Scientific Letters and Papers of James Clerk Maxwell: 1846-1862» Vol. 1, Cambridge University Press. 1990
[8]. Maxwell J.C. A Treatise on Electricity and Magnetism. Vol. 1. Dower, New York. 1954
[9]. Maxwell J.C. On Governors. Proc. Royal Soc. London. 1868, V.16: pp. 270–283.
[10]. Sturm R. Über die Punkte kleinster Entfernungssumme von gegebenen Punkten. J. Reine Angew. Math., V. 97, pp.49-61, 1884.
[11]. Uteshev A.Yu. Analytical Solution for the Generalized Fermat-Torricelli Problem. Amer.Math.Monthly. V. 121, N 4, pp.318-331, 2014. Текст ☞ ЗДЕСЬ (pdf)
[12]. Uteshev A.Yu., Yashina M.V. Stationary Points for the Family of Fermat-Torricelli-Coulomb-like potential functions. Proc. 15th Workshop CASC (Computer Algebra in Scientific Computing), Berlin 2013. Springer. Lecture Notes in Computer Science. V.8136 pp. 412-426, 2013.
[13]. Uteshev A.Yu., Yashina M.V. On Maxwell’s Conjecture for Coulomb Potential Generated by Point Charges. Springer. Transactions on Computational Sciences XXVII. Lecture Notes in Computer Science. V. 9570, pp. 68-80, 2016. Текст ☞ ЗДЕСЬ (pdf)
[14]. Weiszfeld E. Sur le point pour lequel la somme des distances de $ n_ $ points donnés est minimum. Tohoku Math. Journal. V. 43, pp. 355–386, 1937.
[15]. Gabrielov A., Novikov D., Shapiro B. Mystery of Point Charges. Proc. London Math. Soc. Ser. 3. V. 95, pp. 443-472, 2007.
Видео:Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Исследовательская работа по математике «Точка Ферма»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Выберите документ из архива для просмотра:
Выбранный для просмотра документ презентация.ppt
Описание презентации по отдельным слайдам:
Исследовательская работа
по теме
«Точка Ферма»
Выполнил: Сафаров Артем
7 класс
Руководитель: Сафарова
Наталья Александровна
д.Новокурупкаевка
Введение
«Лучший способ изучить что-либо – это открыть самому»
Д.Пойа (1887 – 1985)
— венгерский математик
Актуальность выбранной темы
Актуальность выбранной темы заключается в том, что хотя замечательные точки треугольника мы начинаем узучать с седьмого класса, но точка, о которой пойдет речь в моей работе, не встречается в школьном курсе геометрии. И поэтому я попытался доступными для меня способами собрать сведения о данной точке, исследовать ее свойства, изучить практическое применение.
Цель исследования:
Найти точку внутри треугольника, сумма расстояний от которой до вершин является наименьшей.
Задачи исследовательской работы:
— организовать поиск, изучение источников информации и отбор материала, представляющего интерес по данной теме;
— исследовать различные способы нахождения данной точки;
— исследовать местонахождение в различных видах треугольников;
— рассмотреть свойства полученной точки;
— показать практическое применение.
Теоретическая часть
Физический эксперимент.
При этом общая длина свисающих частей нитей стала наибольшей, а сумма расстояний от узла до отверстий — наименьшей. В этот момент, на узел будут действовать три уравновешивающие друг друга силы, направленные вдоль нитей, углы между нитями окажутся равными. Отметив точку, в которой остановился узел, я увидел, что эта точка не совпадает ни с одной из построенных замечательных точек.
Точка Ферма — Торричелли.
Пьер Ферма (1601-1665) — французский математик, один из создателей аналитической геометрии и теории чисел, автор работ в области теории вероятностей, оптики, исчислении бесконечно малых величин. Он решал задачу о местоположении в треугольнике АВС такой точки F, что сумма FA+FB+FC её расстояний до вершин была бы минимальной.
Определение точки Ферма
Точкой Ферма называется такая точка треугольника, сумма расстояний от которой до вершин треугольника является минимальной. Когда все углы треугольника меньше 120°, то точка Ферма — это такая точка F в треугольнике, из которой все стороны треугольника видны под одним и тем же углом 120°.
Практическая часть
Алгоритм построения
Построить произвольный треугольник ABC.
Построить на его сторонах вне него правильные треугольники ABC1, BCA1, CAB1 .
Провести прямые AA1, BB1, CC1. Точка их пересечения F – искомая.
Расположение точки Ферма в различных видах треугольников.
В прямоугольном треугольнике.
В треугольнике с углом в 120º.
В треугольнике с углом больше 120º.
Свойства точки Ферма
«В огромном саду геометрии каждый найдёт букет себе по вкусу»
Д.Гильберт(1862-1945)-немецкий математик.
1.Из точки Ферма все стороны треугольника видны под углом 120º.
2.Окружности, описанные вокруг правильных треугольников пересекаются в точке Ферма.
3.Ещё одно свойство точки Ферма
Применение точки Ферма.
«Рано или поздно всякая правильная математическая идея находит применение в том или ином деле».
Академик А.Н.Крылов(1863-1945)
Решение следующих задач приводит к нахождению точки Ферма.
Жители трёх домов деревни Новокурупкаевка, расположенных в вершинах треугольника, решили пробурить общую скважину. При этом они хотят расположить скважину в таком месте, чтобы общие затраты на приобретение труб для подведения воды были как можно меньше. Где следует вырыть колодец?
Тренер футбольной команды «Барселона» Жозе Моуринью хочет минимизировать расстояние между полузащитниками. Чтобы добиться этого, игроки должны расположиться следующим образом: Хаби Алонсо в центре поля, Ди Мария – внизу справа, Криштиану Роналду – внизу слева. Месут Озил будет играть промежуточное положение между этими тремя игроками.
В магазине «Электроника» три отдела. Где расположить рабочее место продавца-консультанта, чтобы сумма расстояний до каждого отдела была наименьшей?
Заключение.
Исторически геометрия начиналась с треугольника, поэтому вот уже два с половиной тысячелетия треугольник является символом геометрии. Удивительно, но треугольник, несмотря на свою кажущуюся простоту, является неисчерпаемым объектом изучения — никто даже в наше время не осмелится сказать, что изучил и знает все о треугольнике. В своей работе я попытался показать, что школьная геометрия может стать тогда интересной, когда в ней появляется глубокое и всестороннее изучение треугольника.
Приложение.
Точка Ферма в мыльных пузырях.
Мыльные пленки стремятся сократится до возможных наименьших размеров. Так как их поверхностное натяжение одинаково, то силы их поверхностного натяжения могут «уравновесить» друг друга лишь в том случае, когда углы, под которыми они пересекаются, равны между собой и, следовательно, каждый равен 120°. После установления равновесия в правильной треугольной пирамиде очень четко была видна точка пересечения сил натяжения, от которой каждое ребро пирамиды было видно под углом 120°. В кубе наблюдалась аналогичная картина. Это похоже на фокус, но это действительно так!
СПАСИБО ЗА ВНИМАНИЕ.
Выбранный для просмотра документ точка ферма.docx
 | ||
СОДЕРЖАНИЕ:
1.Физический эксперимент. 3 стр.
2.Проверка гипотезы. 3 стр.
3.Точка Ферма-Торричелли. 4 стр.
4.Определение точки Ферма. 4 стр.
1.Алгоритм построения точки Ферма. 4 стр.
2.Расположение точки Ферма в различных видах треугольников. 6 стр.
3. Свойства точки Ферма. 8 стр.
Применение точки Ферма. 12 стр.
Заключение. 13 стр.
Приложение 1. 14 стр.
Приложение 2. 16 стр.
«Лучший способ изучить что- либо – это открыть самому»
Д. Пойа (1887 – 1985)- венгерский математик²
На занятиях дистанционной школы по геометрии мы изучали тему «Замечательные точки треугольника» и выполняли построения в компьютерной среде «Живая математика». Взяв различные точки среди множества точек внутри треугольника, я увидел, что сумма расстояний от этих точек до вершин треугольника менялась. Тогда я выдвинул гипотезу, что может быть, среди этих точек есть точка, сумма расстояний от которой до вершин треугольника является минимальной.
Актуальность выбранной темы заключается в том, что хотя замечательные точки треугольника мы начинаем изучать с седьмого класса, но точка, о которой пойдет речь в моей работе, не встречается в школьном курсе геометрии. И поэтому я попытался доступными для меня способами собрать сведения о данной точке, исследовать ее свойства, изучить практическое применение. На мой взгляд, получился интересный материал.
Цель моего исследования: Найти точку внутри треугольника, сумма расстояний от которой до вершин является наименьшей.
§ организовать поиск, изучение источников информации и отбор материала, представляющего интерес по данной теме;
§ исследовать различные способы нахождения данной точки;
§ исследовать местонахождение в различных видах треугольников;
§ рассмотреть свойства полученной точки;
§ показать практическое применение.
Ценность моей работы я считаю в том, что мне удалось показать насколько может быть интересной и содержательной геометрия. Также я рассмотрел способы построения точки Ферма в треугольниках различных видов.

Нарисовав остроугольный (разносторонний) треугольник на листе плотного картона и отметив точки пересечения биссектрис, медиан и высот, я проделал отверстия на месте вершин. Взял три нитки, привязал к каждой одинаковые грузы, продел их концы в отверстия и связал их свободные концы в узел. После отпускания грузов нити натянулись. При этом общая длина свисающих частей нитей стала наибольшей, а сумма расстояний от узла до отверстий — наименьшей. В этот момент, на узел будут действовать три уравновешивающие друг друга силы, направленные вдоль нитей, углы между нитями окажутся равными. Отметив точку, в которой остановился узел, я увидел, что эта точка не совпадает ни с одной из построенных замечательных точек.
2 . Проверка гипотезы.
Далее, я измерил сумму расстояний от этой точки до вершин треугольника, от отмеченных замечательных точек и двух произвольно взятых точек (приложение 2), результаты записал в виде таблицы. Сравним полученные результаты.
Сумма расстояний от точки до вершин треугольника
S — точка пересечения биссектрис
SA + SB + SC = 0,223 м
M — точка пересечения медиан
H – точка пересечения высот
P — произвольная точка
K — произвольная точка
По данным таблицы ясно, что в последнем случае сумма расстояний наименьшая.
3. Точка Ферма — Торричелли.
Эта точка называется точкой Ферма по имени французского математика 
Оказывается, этим вопросом интересовались и другие учёные в XVIII веке. Эта точка в треугольнике связана с именами еще двух выдающихся учёных прошлого. Швейцарский геометр Якоб Штейнер рассматривал ту же проблему в несколько более общем виде: он пытался найти кратчайшую сеть дорог, соединяющих три пункта. Точку треугольника, положение которой удовлетворяет этим условиям, построил итальянский учёный Эванджелиста Торричелли, известный как изобретатель ртутного барометра.
4. Определение точки Ферма.
Точкой Ферма называется такая точка треугольника, сумма расстояний от которой до вершин треугольника является минимальной. Когда все углы треугольника меньше 120°, то точка Ферма – это такая точка F в треугольнике, из которой все стороны треугольника видны под одним и тем же углом 120°.
1. Алгоритм построения.
Чтобы получить точку Ферма нужно:
v Построить произвольный остроугольный треугольник ABC .
v Построить на его сторонах вне него правильные треугольники ABC1, BCA1, CAB1 .
v Провести прямые AA1, BB1, CC1. Точка их пересечения F – искомая.
Вывод: В остроугольном треугольнике точка Ферма находится внутри треугольника.
2. Расположение точки Ферма в различных видах треугольников.
Исследуем, как будет располагаться точка Ферма в различных видах треугольников.
Ø В равностороннем треугольнике.
В равностороннем треугольнике, как известно, медианы, биссектрисы и высоты пересекаются в одной точке. Точка Ферма будет совпадать с этой точкой.
Ø В прямоугольном треугольнике.
Искомая точка находится внутри треугольника.
Ø В треугольнике с углом в 120º.
Если один из углов треугольника равен 120 градусов, то точка Ферма совпадет с вершиной треугольника.
Ø В треугольнике с углом больше 120º.
Если один из углов треугольника больше 120º, то точка Ферма находится вне треугольника.
В треугольнике, у которого углы меньше 120º, точка Ферма находится внутри треугольника.
В треугольнике, с углом больше 120º, точка Ферма находится вне треугольника.
3. Свойства точки Ферма.
«В огромном саду геометрии каждый найдёт букет себе по вкусу»
Ø Из точки Ферма все стороны видны под углом 120º.
Ø Окружности, описанные вокруг правильных треугольников пересекаются в точке Ферма.
Ø Если внутри треугольника построить треугольник, стороны которого являются средними линиями исходного треугольника, потом аналогично построить третий, четвертый треугольник и т.д.; в каждом треугольнике построить свою точку Ферма, то все точки Ферма будут лежать на одной прямой.
а) Построим произвольный треугольник и точку Ферма данного треугольника.
б) В заданном треугольнике построим треугольник, стороны которого являются средними линиями исходного (красный треугольник).
в) Построим точку Ферма в красном треугольнике.
г) Построим треугольник, стороны которого являются средними линиями красного (зеленый треугольник) и найдем для него точку Ферма.
Применение точки Ферма.
«Рано или поздно всякая правильная математическая
идея находит применение в том или ином деле».²
Решение следующих задач приводит к нахождению точки Ферма.
1. Жители трех домов деревни Новокурупкаевка, расположенных в вершинах треугольника, решили пробурить общую скважину. При этом они хотят расположить скважину в таком месте, чтобы общие затраты на приобретение труб для подведения воды были как можно меньше. Где следует вырыть колодец?
2. Тренер футбольной команды «Барселона» Жозе Моуринью хочет минимизировать расстояние между полузащитниками. Чтобы добиться этого, игроки должны расположиться следующим образом: Хаби Алонсо в центре поля, Ди Мария – внизу справа, Криштиану Роналду – внизу слева. Месут Озил будет играть промежуточное положение между этими тремя игроками.
3. В магазине «Электроника» три отдела. Где расположить рабочее место продавца-консультанта, чтобы сумма расстояний до каждого отдела была наименьшей?
Исторически геометрия начиналась с треугольника, поэтому вот уже два с половиной тысячелетия треугольник является символом геометрии. Удивительно, но треугольник, несмотря на свою кажущуюся простоту, является неисчерпаемым объектом изучения – никто даже в наше время не осмелится сказать, что изучил и знает все о треугольнике. В своей работе я попытался показать, что школьная геометрия может стать тогда интересной, когда в ней появляется глубокое и всестороннее изучение треугольника.
2.mar 1965 4810.narod.ru
5. ru . wikipedia . org
Приложение 1. Точка Ферма в мыльных пузырях.

Так выглядит точка Ферма в мыльных пузырях.
Видео:Задача МишустинаСкачать
 Некоторые малоизвестные факты из геометрии треугольника
Некоторые малоизвестные факты из геометрии треугольника
Статья представляет собой дополнение к очень популярной теме «Геометрия треугольника». В ней рассматриваются некоторые известные факты с оригинальными авторскими доказательствами. Некоторые пункты можно разобрать дополнительно к отдельным темам: вписанная окружность, теорема Пифагора, векторный метод, точка Ферма, треугольники Наполеона. В конце каждого пункта приводятся упражнения, позволяющие закрепить рассматриваемые темы, уяснить их с разных сторон. Во многих случаях сами упражнения содержат важный теоретический материал. Многие упражнения взяты из известных учебников.
1. Симметричный вывод формулы Герона
Точки касания вписанной окружности со сторонами треугольника обозначим через A1, B1, C1 (рис. 1). Треугольники AIB1 и AIC1, BIA1 и BIC1, CIA1 и CIB1 попарно равны, как прямоугольные треугольники, имеющие общую гипотенузу и равные углы.
откуда AB1 = AC1 = 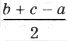
Аналогично CA1 = CB1 =
и BA1 = BC1 = 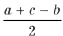
Обозначим углы Р C1IB1 = a , Р C1IA1 = b , Р A1IB1 = g . В D AIB1 катеты связаны соотношением
откуда
.
Аналогично
.
Так как
,
то легко доказать
(*)
Подставив в (*) выражения
через a, b, c и r, получим
= ,
откуда
Так как SABC = rp, то отсюда следует формула Герона.
.
Здесь и далее через R обозначен радиус описанной окружности.
3. Докажите, что в D ABC биссектриса угла A, средняя линия, параллельная AC, и прямая, соединяющая точки касания вписанной окружности со сторонами CB и CA, пересекаются в одной точке.
4. Докажите, что сумма квадратов расстояний от точек касания вписанной в треугольник окружности с его сторонами до центра описанной равна 3R 2 – 4Rr – r 2 .
5. Центр окружности, вписанной в прямоугольный треугольник, находится на расстоянии и см от концов гипотенузы. Найдите катеты этого треугольника.
6. В D ABC известно BC = a, Р A = a , Р B = b . Найдите радиус окружности, пересекающей все его стороны и высекающей на каждой из них хорды длины d.
7. В D ABC проведена медиана AM. Может ли радиус окружности, вписанной в D ABM, быть ровно в два раза больше радиуса окружности, вписанной в D ACM?
8*. Окружность, вписанная в D ABC, делит медиану BM на три равные части. Найдите отношение BC : CA : AB.
2. К теореме Пифагора
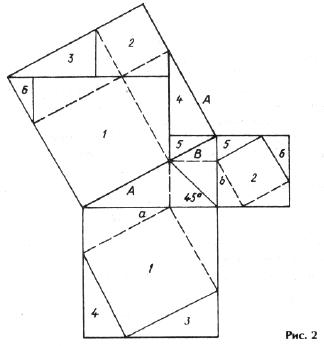
Многие доказательства теоремы Пифагора используют характерный рисунок квадратов, построенных во внешнюю стороны на сторонах треугольника («Пифагоровы штаны»).
Доказательство сводится к доказательству формулы
где S – площадь квадрата, построенного на гипотенузе, S1, S2 – площади квадратов, построенных на катетах.
Обычно при этом используется разбиение квадратов на равные части, совмещающиеся друг с другом.
Минимальное число фигур разбиения – 5 (Ан-Нариций, древнеиндийское «колесо с лопастями»), бывает 7 и 8). На рис. 2 показано разбиение, в котором совмещается 6 фигур.
Биссектриса прямого угла исходного треугольника делит гипотенузу на части длиной A и B, причем по свойству биссектрисы A : B = a : b, где a и b – длины катетов.
Проведем в квадрате, построенном на гипотенузе, штриховые линии на расстоянии A и B от сторон. Рассмотрим выделенный жирным контуром прямоугольный треугольник. Он подобен исходному, так как его катеты A и B пропорциональны a и b. Поэтому гипотенуза выделенного треугольника параллельна катету b, так как соответствующие накрест лежащие углы равны. Теперь можно провести остальные линии разбиения: в квадрате, построенном на гипотенузе, – параллельно катетам, а в квадратах, построенных на катетах, – параллельно сторонам квадрата, построенного на гипотенузе (причем во втором случае длины отрезков разбиения равны A и B). Нетрудно видеть, что при этом получаются совмещающиеся фигуры.
1. Высота, опущенная на гипотенузу, делит прямоугольный треугольник на два, подобных исходному. Пользуясь тем, что площади подобных фигур относятся как квадраты их линейных элементов, докажите теорему Пифагора (Ч. Тригг).
2. Впишем в прямоугольный треугольник окружность, которая точками касания делит катеты на отрезки, два из которых по длине совпадают с r – радиусом окружности. Пользуясь результатами п. 1, еще раз докажите теорему Пифагора (доказательство Мёльманна).
3. Точки O1, O2, O3 – соответственно центры квадратов, построенных на катете и гипотенузе, C – вершина прямого угла исходного треугольника. Докажите, что отрезки O1O2 и O3C перпендикулярны, а их длины равны.
4. Найдите площадь O1O2O3 (см. упражнение 3), если длины катетов прямоугольного треугольника равны a и b.
3. Теорема Лейбница
Если O – точка пересечения медиан D ABC, P – произвольная точка плоскости, то (рис. 3)
Доказательство. Возведем векторное равенство
Аналогично получаются равенства:
Складывая эти три равенства, получаем
так как сумма векторов в скобках равна нулю. Отсюда
Так как
то отсюда следует доказываемая формула.
Дополнительное упражнение. Получите формулы для медиан треугольника
1. Докажите, что сумма квадратов расстояний от произвольной точки плоскости до вершины треугольника является минимальной, если точка совпадает с точкой пересечения медиан.
2. Вычислите расстояние от точки пересечения медиан до центра описанной окружности.
3. Вычислите расстояние от точки пересечения медиан до центра вписанной окружности.
4. Докажите, что для произвольной точки P, лежащей на окружности, вписанной в равносторонний D ABC,
PA 2 + PB 2 + PC 2 = const.
5. Полупериметр D ABC равен p. Докажите, что для любой точки M плоскости имеет место неравенство
причем равенство достигается лишь в случае, когда ABC – правильный треугольник и M – его центр.
6*. Радиус круга, описанного около треугольника, равен R. Расстояние от центра этого круга до точки пересечения медиан треугольника равно d. Найдите произведение площади данного треугольника и треугольника, образованного прямыми, проходящими через его вершины перпендикулярно медианам, из этих вершин выходящим. Указание. Если O – точка пересечения медиан исходного D ABC, то отрезки OA, OB, OC делят второй больший треугольник на 3 вписанных четырехугольника, площади которых можно выразить через стороны и площади треугольников AOB, AOC, BOC, а, значит, – ABC.
7*. Пусть ABC – правильный треугольник со стороной a, M – некоторая точка плоскости, находящаяся на расстоянии d от центра треугольника ABC. Докажите, что площадь треугольника, стороны которого равны отрезкам MA, MB и MC, выражается формулой
Точкой Ферма называется такая точка треугольника, сумма расстояний от которой до вершин треугольника является минимальной. Когда все углы треугольника меньше 120°, то точка Ферма – это такая точка F в треугольнике, из которой все стороны треугольника видны под одним и тем же углом 120°.
Доказательство. Проведем через вершины исходного D ABC прямые, перпендикулярные отрезкам AF, BF и CF соответственно. Они пересекутся в вершинах некоторого правильного треугольника A1B1C1. Для любой точки P D A1B1C1 сумма длин перпендикуляров, опущенных из P на стороны этого треугольника, есть постоянное число (в частности, оно равно AF + BF + CF), так как она равна , где S – площадь A1B1C1, a – его сторона. Очевидно, что PA не меньше длины перпендикуляра, опущенного из P на сторону B1C1, проходящую через A. Тем более, PA + PB + PC не меньше суммы длин всех перпендикуляров, которая равна AF + BF + CF, и равенство достигается, когда P совпадает с F.
Иногда точку Ферма называют точкой Торичелли или точкой Брокара.
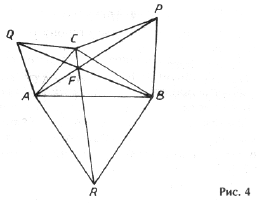
Чтобы построить точку Ферма, надо на сторонах D ABC во внешнюю сторону построить равносторонние треугольники ABR, BCP и ACQ. Отрезки AP, BQ и CR пересекаются в точке F – точке Ферма (рис. 4).
Действительно, пусть AP и BQ пересекаются в точке F. При повороте вокруг точки C на 60° D CQB переходит в D CAP. Следовательно, угол между QB и AP Р QFA = 60°, и точка F лежит на окружности, описанной около D AQC. Аналогично угол Р PFB = 60°, и точка F лежит на окружности, описанной около D BPC. Так как угол Р AFB = 120°, то точка F лежит на окружности, описанной около D ABR, значит, Р AFR = 60°. Так как при повороте на 60° вокруг точки B D APB переходит в D RCB, то угол между AP и CR равен 60° и точка F лежит на CR.
1. Используя теорему Птолемея для четырехугольника AFBR и обозначив расстояния от F до вершин D ABC через x1, x2, x3, найдите AP = BQ = CR (рис. 4).
5. Треугольники Наполеона
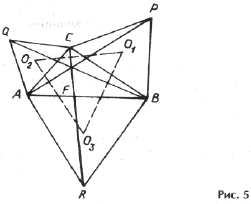
Если на сторонах D ABC внешним образом построить равносторонние треугольники, то их центры являются вершинами равностороннего внешнего треугольника Наполеона.
Действительно, вершины D O1O2O3 являются центрами окружностей, описанных вокруг равносторонних треугольников и пересекающихся в точке F. Поэтому стороны D O1O2O3 перпендикулярны отрезкам FA, FB и FC, и углы между ними равны 60° (рис. 5).
Если на сторонах D ABC построить равносторонние треугольники во внутреннюю сторону и соединить их центры, то получится равносторонний внутренний треугольник Наполеона.
Применив теорему косинусов к D CO1O2, можно вывести формулу для стороны внешнего треугольника Наполеона:
где S – площадь D ABC.
Для стороны внутреннего треугольника Наполеона аналогично получается
1. Докажите, что центры треугольников Наполеона совпадают с точкой пересечения медиан (для этого вычислите расстояние от какой-нибудь вершины треугольника Наполеона до точки пересечения медиан и покажите, что оно на зависит от рассматриваемой величины и равно

где l – длина стороны треугольника Наполеона).2. Докажите, что разность площадей треугольников Наполеона (внешнего и внутреннего) равна площади D ABC.
3. Докажите, что
4. Применив теорему Лейбница для внешнего треугольника Наполеона и точки Ферма F, вычислите расстояние от точки пересечения медиан, которая является центром треугольника Наполеона, до точки Ферма.
5. Докажите, что
6. Докажите, что PQ 2 + QR 2 + RP 2 = a 2 + b 2 + c 2 + 9l1 2 .
7. Докажите, что точка пересечения медиан D PQR совпадает с точкой G пересечения медиан D ABC.
Указание. Вычислите длины PG, QG, RG и примените теорему Лейбница; второй способ – докажите, что векторная сумма
8. На сторонах треугольника во внешнюю сторону построены квадраты. Докажите, что точка пересечения медиан треугольника с вершинами в центрах этих квадратов совпадает с точкой пересечения медиан данного треугольника.
(См. указание к упр. 7, второй способ.)
9. Рассмотрим центроиды A1, B1, C1 треугольников AQR, BPR и CQP соответственно. Докажите, что D A1B1C1 – правильный и центр его совпадает с центроидом G данного D ABC.
Указание. Докажите, что равны векторы
10. Докажите, что треугольники A1B1C1 и O1O2O3 симметричны относительно их общего центра G и поэтому шестиугольник O1C1O2A1O3B1 – правильный и его центр совпадает с центроидом G данного треугольника. Сторона этого шестиугольника
.
11. Докажите, что середины A2, B2, C2 отрезков AO1, BO2, CO3 являются вершинами еще одного равностороннего треугольника он гомотетичен внутреннему треугольнику Наполеона с
.
12*. Пусть A3, B3, C3 – середины отрезков QR, PR и QP соответственно. Докажите, что прямые AA3, BB3, CC3 пересекаются в одной точке или параллельны.
13. Докажите, что если подобные треугольники PCB, CQA, BAR построены извне на сторонах произвольного D ABC, то окружности, описанные вокруг этих трех треугольников, имеют общую точку.
14. Докажите, что в условиях упражнения 13 центры трех указанных окружностей образуют треугольник, подобный треугольникам PCB, CQA, BAR.
15. Докажите, что если на двух сторонах треугольника построены квадраты, то окружности, описанные вокруг них, пересекаются на окружности, построенной на третьей стороне, как на диаметре, и центры этих трех окружностей являются вершинами равнобедренного прямоугольного треугольника.
16. Докажите, что прямые AO1, BO2, CO3 пересекаются в одной точке (см. рис. 5).
Указание. Продолжить эти прямые до пересечения со сторонами треугольника ABC и применить теорему Чевы.
6. Расстояние от точки Ферма до центра описанной окружности
Ранее было получено, что
где
l1 – длина стороны внешнего треугольника Наполеона (упражнения 4.1, 4.2 и 5.5).
•. (1)
Точка Ферма F лежит на прямой CC1, которая соединяет вершину C исходного D ABC с вершиной C1 равностороннего D ABC1 (рис. 6); O – центр описанной окружности.
Обозначим угол BCC1 через j ;

С учетом этого преобразуем формулу (2):
Найдем по теореме косинусов для D BCC1
Для a (применим теоремы косинусов и синусов к D ABC)
Подставив полученные выражения в (3), находим
Тогда с учетом (1) получим
(4)
(5)
которую преобразуем к виду
(6)
где d – расстояние от точки пересечения медиан до центра описанной окружности.
Дополнение: точка F1 пересечения прямых AP ‘, BO ‘ и CR ‘, где ABR ‘, BCP ‘ и ACO ‘ – равносторонние треугольники, построенные на сторонах D ABC во внутреннюю сторону, является точкой, двойственной точке Ферма. Точка F1 лежит на окружности, описанной около внешнего треугольника Наполеона. Расстояние между точками F и F1 равно (без доказательства)
1. Докажите, что расстояние от точки Ферма F до центра описанной окружности O больше расстояния от точки пересечения медиан G до центра описанной окружности O.
2. Вычислите угол Р OGF в обозначениях упражнения 1 и формулы (6).
3. Доказать, что
4*. Точка F – точка Ферма D ABC (углы которого меньше 120°). Докажите, что прямые Эйлера треугольников AFB, BFC и CFA пересекаются в одной точке.
📽️ Видео
✓ Малая теорема Ферма или задачка про бусы | Ботай со мной #013 | Борис Трушин !Скачать
Высшая математика. Теорема Ферма, Ролля, Лагранжа, КошиСкачать
Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать
Задачи на доказательство делимости. Малая теорема Ферма | Ботай со мной #036 | Борис Трушин !Скачать

































 Некоторые малоизвестные факты из геометрии треугольника
Некоторые малоизвестные факты из геометрии треугольника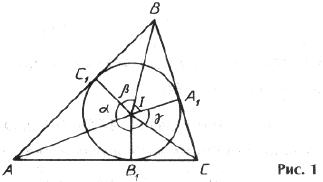
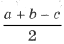
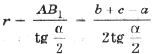
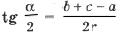 .
.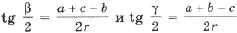 .
.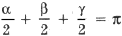 ,
,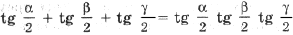 (*)
(*)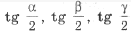
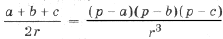 = ,
= ,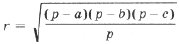
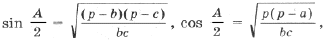
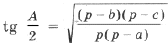 .
.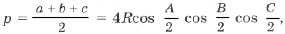
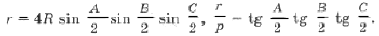
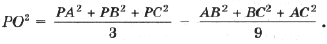

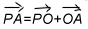
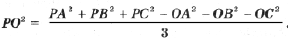
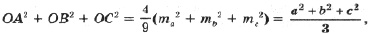
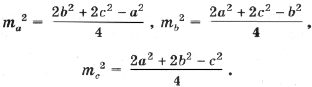
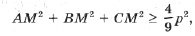
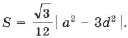
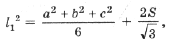
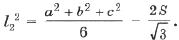
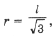
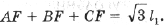
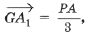
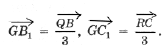
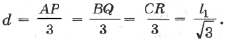 .
. .
.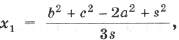
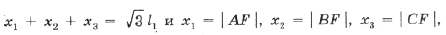

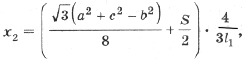
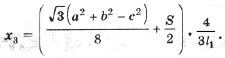 •. (1)
•. (1)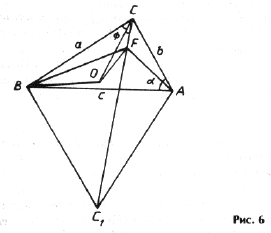
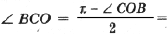
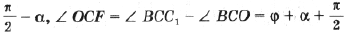
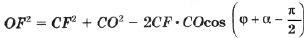
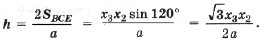
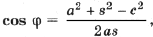
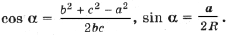
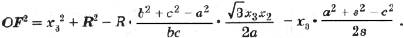
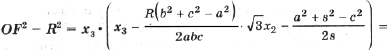
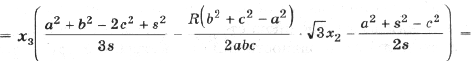
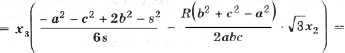
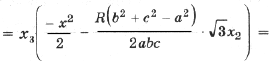
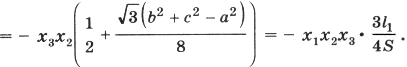
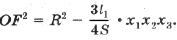 (4)
(4)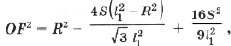 (5)
(5)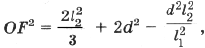 (6)
(6)