Треугольник Паскаля — иными словами, бесконечная числовая таблица, выполненная в форме треугольника, — прост, изящен и велик, как все гениальное: каждое число его равно сумме двух чисел, которые расположены над ним. Нетрудно догадаться, что этот треугольник может быть каким угодно большим — его можно продолжать беспредельно.
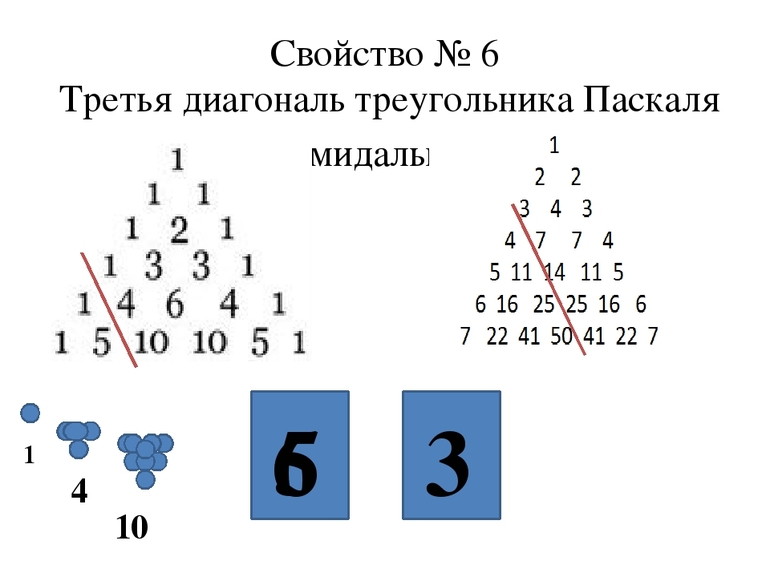
Первый ряд чисел (если считать своеобразные «диагонали» от вершины) — это единицы, второй ряд содержит натуральные числа, соответствующие номеру строки расположения числа. Все числа третьего ряда — 1, 3, 6, 10, 15, 21,28, 36, 45 и т.д. представляют собой треугольные числа, которые показывают, какое именно количество предметов (подобно шарам в бильярде) могут в совокупности образовать треугольник. Этот ряд замечателен еще и тем, что каждое его число является суммой натурального ряда чисел, например: 45 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 или 21 = 1 + 2 + 3 + 4 + 5 + 6 и т.д. Четвертый ряд чисел треугольника Паскаля (1, 4, 10, 20, 35, 56 и т.д.) содержит тетраэдрические (пирамидальные) числа, которые участвуют в воображаемом «строительстве» тетраэдра: на три уже имеющихся шара кладется еще один шар и получается — 4 и т.д. Пятый ряд треугольника, образованный гипертетраэдрическими числами 1, 5, 15, 35, 70 и т.д., поможет получить в воображении (поскольку возможен только в четырехмерном пространстве) гипертетраэдр: один шар объединяется с четырьмя, а те — с десятью и т.д. Еще более невообразимый пятимерный тетраэдр «выстраивается» с помощью чисел шестого ряда треугольника Паскаля: 1, 6, 21, 56, 126 и т.д.
Что касается горизонтальных линий, то все числа этих строк являются биномиальными коэффициентами, имеющими бесценное значение для комбинаторики, теории вероятностей, родоначальником которой в «соавторстве» с Ферма стал Б. Паскаль, и иных математических областей.
Одним из загадочных свойств треугольника Паскаля является быстрота нахождения суммы чисел ряда от начала до нужного нам числа. Для этого необходимо, найдя последнее слагаемое, обратить внимание на число, которое записано снизу и слева (если нумеровать ряды с правой стороны) или справа (если нумеровать ряды с левой стороны) от последнего слагаемого. Например, чтобы узнать, что в сумме дадут нам все числа четвертого ряда от 1 до 56, достаточно, найдя 56, взглянуть, что написано слева внизу: это число 126. Удивительно верно!
Кроме того, не догадываясь о собственном открытии (это было обнаружено только в XIX веке), Паскаль «зашифровал» в треугольнике известные числа последовательности Фибоначчи: 1, 6, 10, 4; 1, 5, 6, 1 и т.д.
Видео:Треугольник ПаскаляСкачать

Треугольник Паскаля — формула, свойства и применение
Видео:Зачем нужен треугольник ПаскаляСкачать

Основная формула
Строки треугольника обычно нумеруются, начиная со строки n = 0 в верхней части. Записи в каждой строке целочисленные и нумеруются слева, начиная с k = 0, обычно располагаются в шахматном порядке относительно чисел в соседних строчках. Построить фигуру можно следующим образом:
- В центре верхней части листа ставится цифра «1».
- В следующем ряду — две единицы слева и справа от центра (получается треугольная форма).
- В каждой последующей строке ряд будет начинаться и заканчиваться числом «1». Внутренние члены вычисляются путём суммирования двух цифр над ним.
Запись в n строке и k столбце паскалевской фигуры обозначается (n k). Например, уникальная ненулевая запись в самой верхней строке (0 0) = 1. С помощью этого конструкция предыдущего абзаца может быть записана следующим образом, образуя формулу треугольника Паскаля (n k) = (n — 1 k-1) + (n — 1 k), для любого неотрицательного целого числа n и любого целого числа k от 0 до n включительно. Трёхмерная версия называется пирамидой или тетраэдром, а общие — симплексами.
Видео:Зачем нужен треугольник Паскаля (спойлер: для формул сокращённого умножения)Скачать

История открытия
Паскаль ввёл в действие многие ранее недостаточно проверенные способы использования чисел треугольника, и он подробно описал их в, пожалуй, самом раннем из известных математических трактатов, специально посвящённых этому вопросу, в труде об арифметике Traité du triangle (1665). За столетия до того обсуждение чисел возникло в контексте индийских исследований комбинаторики и биномиальных чисел, а у греков были работы по «фигурным числам».
Из более поздних источников видно, что биномиальные коэффициенты и аддитивная формула для их генерации были известны ещё до II века до нашей эры по работам Пингала. К сожалению, бо́льшая часть трудов была утеряна. Варахамихира около 505 года дал чёткое описание аддитивной формулы, а более подробное объяснение того же правила было дано Халаюдхой (около 975 года). Он также объяснил неясные ссылки на Меру-прастаара, лестницы у горы Меру, дав первое сохранившееся определение расположению этих чисел, представленных в виде треугольника.
Примерно в 850 году джайнский математик Махавира вывел другую формулу для биномиальных коэффициентов, используя умножение, эквивалентное современной формуле. В 1068 году Бхаттотпала во время своей исследовательской деятельности вычислил четыре столбца первых шестнадцати строк. Он был первым признанным математиком, который уравнял аддитивные и мультипликативные формулы для этих чисел.
Примерно в то же время персидский учёный Аль-Караджи (953–1029) написал книгу (на данный момент утраченную), в которой содержалось первое описание треугольника Паскаля. Позднее работа была переписана персидским поэтом, астрономом и математиком Омаром Хайямом (1048–1131). Таким образом, в Иране фигура упоминается как треугольник Хайяма.
Известно несколько теорем, связанных с этой темой, включая биномы. Хайям использовал метод нахождения n-x корней, основанный на биномиальном разложении и, следовательно, на одноимённых коэффициентах. Треугольник был известен в Китае в начале XI века благодаря работе китайского математика Цзя Сианя (1010–1070). В XIII веке Ян Хуэй (1238–1298) представил этот способ, и поэтому в Китае он до сих пор называется треугольником Ян Хуэя.
На западе биномиальные коэффициенты были рассчитаны Жерсонидом в начале XIV века, он использовал мультипликативную формулу. Петрус Апиан (1495–1552) опубликовал полный треугольник на обложке своей книги примерно в 1527 году. Это была первая печатная версия фигуры в Европе. Майкл Стифель представил эту тему как таблицу фигурных тел в 1544 году.
В Италии паскалевский треугольник зовут другим именем, в честь итальянского алгебраиста Никколо Фонтана Тарталья (1500–1577). Вообще, современное имя фигура приобрела благодаря Пьеру Раймонду до Монтрмору (1708), который назвал треугольник «Таблица Паскаля для сочетаний» (дословно: Таблица мистера Паскаля для комбинаций) и Абрахамом Муавром (1730).
Видео:Несколько красивых свойств треугольника ПаскаляСкачать
Отличительные черты
Треугольник Паскаля и его свойства — тема довольно обширная. Главное, в нём содержится множество моделей чисел. Обзор следует начать с простого — ряды:
- Сумма элементов одной строки в два раза больше суммы строки, предшествующей ей. Например, строка 0 (самая верхняя) имеет значение 1, строчка 1–2, а 2 имеет значение 4 и т. д. Это потому что каждый элемент в строке производит два элемента в следующем ряду: один слева и один справа. Сумма элементов строки n равна 2 n .
- Принимая произведение элементов в каждой строке, последовательность продуктов можно связать с основанием натурального логарифма.
- В треугольнике Паскаля через бесконечный ряд Нилаканты можно найти число Пи.
- Значение строки, если каждая запись считается десятичным знаком (имеется в виду, что числа больше 9 переносятся соответственно), является степенью 11 (11 n для строки n). Таким образом, в строке 2 ⟨1, 2, 1⟩ становится 11 2 , равно как ⟨1, 5, 10, 10, 5, 1⟩ в строке пять становится (после переноса) 161, 051, что составляет 11 5 . Это свойство объясняется установкой x = 10 в биномиальном разложении (x + 1) n и корректировкой значений в десятичной системе.
- Некоторые числа в треугольнике Паскаля соотносятся с числами в треугольнике Лозанича.
- Сумма квадратов элементов строки n равна среднему элементу строки 2 n. Например, 1 2 + 4 2 + 6 2 + 4 2 + 1 2 = 70.
- В любой строчке n, где n является чётным, средний член за вычетом члена в двух точках слева равен каталонскому числу (n / 2 + 1).
- В строчке р, где р представляет собой простое число, все члены в этой строке, за исключением 1s, являются кратными р.
- Чётность. Для измерения нечётных терминов в строке n необходимо преобразовать n в двоичную форму. Пусть x будет числом 1s в двоичном представлении. Тогда количество нечётных членов будет 2 х . Эти числа являются значениями в последовательности Гулда.
- Каждая запись в строке 2 n -1, n ≥ 0, является нечётной.
- Полярность. Когда элементы строки треугольника Паскаля складываются и вычитаются вместе последовательно, каждая строка со средним числом, означающим строки с нечётным числом целых чисел, даёт 0 в качестве результата.
Диагонали треугольника содержат фигурные числа симплексов. Например:
- Идущие вдоль левого и правого краёв диагонали содержат только 1.
- Рядом с рёбрами диагонали содержат натуральные числа по порядку.
- Двигаясь внутрь, следующая пара содержит треугольные числа по порядку.
- Следующая пара — тетраэдрические, а следующая пара — числа пятиугольника.
Существуют простые алгоритмы для вычисления всех элементов в строке или диагонали без вычисления других элементов или факториалов.
Видео:ТРЕУГОЛЬНИК ПАСКАЛЯ 😊 ЧАСТЬ I #shorts #математика #егэ #задачи #задачаналогику #егэ2022 #огэ2022Скачать

Общие свойства
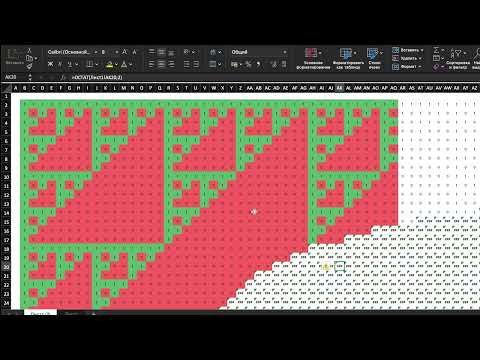
Образец, полученный путём раскраски только нечётных чисел, очень похож на фрактал, называемый треугольником Серпинского. Это сходство становится всё более точным, так как рассматривается больше строк в пределе, когда число рядов приближается к бесконечности, получающийся в результате шаблон представляет собой фигуру, предполагающую фиксированный периметр. В целом числа могут быть окрашены по-разному в зависимости от того, являются ли они кратными 3, 4 и т. д.
В треугольной части сетки количество кратчайших путей от заданного до верхнего угла треугольника является соответствующей записью в паскалевском треугольнике. На треугольной игровой доске Плинко это распределение должно давать вероятности выигрыша различных призов. Если строки треугольника выровнены по левому краю, диагональные полосы суммируются с числами Фибоначчи.
Благодаря простому построению факториалами можно дать очень простое представление фигуры Паскаля в терминах экспоненциальной матрицы: треугольник — это экспонента матрицы, которая имеет последовательность 1, 2, 3, 4… на её субдиагонали, а все другие точки — 0.
Количество элементов симплексов фигуры можно использовать в качестве справочной таблицы для количества элементов (рёбра и углы) в многогранниках (треугольник, тетраэдр, квадрат и куб).
Шаблон, созданный элементарным клеточным автоматом с использованием правила 60, является в точности паскалевским треугольником с биномиальными коэффициентами, приведёнными по модулю 2. Правило 102 также создаёт этот шаблон, когда завершающие нули опущены. Правило 90 создаёт тот же шаблон, но с пустой ячейкой, разделяющей каждую запись в строках. Фигура может быть расширена до отрицательных номеров строк.
Видео:Бином Ньютона и треугольник Паскаля | Учитель года Москвы — 2020Скачать

Секреты треугольника
Конечно, сейчас большинство расчётов для решения задач не в классе можно сделать с помощью онлайн-калькулятора. Как пользоваться треугольником Паскаля и для чего он нужен, обычно рассказывают в школьном курсе математики. Однако его применение может быть гораздо шире, чем принято думать.
Начать следует со скрытых последовательностей. Первые два столбца фигуры не слишком интересны — это только цифры и натуральные числа. Следующий столбец — треугольные числа. Можно думать о них, как о серии точек, необходимых для создания групп треугольников разных размеров.
Точно так же четвёртый столбец — это тетраэдрические числа или треугольные пирамидальные. Как следует из их названия, они представляют собой раскладку точек, необходимых для создания пирамид с треугольными основаниями.
Столбцы строят таким образом, чтобы описывать «симплексы», которые являются просто экстраполяциями идеи тетраэдра в произвольные измерения. Следующий столбец — это 5-симплексные числа, затем 6-симплексные числа и так далее.
Полномочия двойки
Если суммировать каждую строку, получатся степени основания 2 начиная с 2⁰ = 1. Если изобразить это в таблице, то получится следующее:
| 1 | ||||||||||||||
| 1 | + | 1 | = | 2 | ||||||||||
| 1 | + | 2 | + | 1 | = | 4 | ||||||||
| 1 | + | 3 | + | 3 | + | 1 | = | 8 | ||||||
| 1 | + | 4 | + | 6 | + | 4 | + | 1 | = | 16 | ||||
| 1 | + | 5 | + | 10 | + | 10 | + | 5 | + | 1 | = | 32 | ||
| 1 | + | 6 | + | 15 | + | 20 | + | 15 | + | 6 | + | 1 | = | 64 |
Суммирование строк показывает силы базы 2.
Силы одиннадцати
Треугольник также показывает силы основания 11. Всё, что нужно сделать, это сложить числа в каждом ряду вместе. Как показывает исследовательский опыт, этого достаточно только для первых пяти строк. Сложности начинаются, когда записи состоят из двузначных чисел. Например:
| 1 | = | 11° |
| 11 | = | 11¹ |
| 121 | = | 11² |
| 1331 | = | 11³ |
Оказывается, всё, что нужно сделать — перенести десятки на одно число слева.
Совершенные квадраты
Если утверждать, что 4² — это 6 + 10 = 16, то можно найти идеальные квадраты натуральных чисел в столбце 2, суммируя число справа с числом ниже. Например:
- 2² → 1 + 3 = 4
- 3² → 3 + 6
- 4² → 6 + 10 = 16 и так далее.
Комбинаторные варианты
Чтобы раскрыть скрытую последовательность Фибоначчи, которая на первый взгляд может отсутствовать, нужно суммировать диагонали лево-выровненного паскалевского треугольника. Первые 7 чисел в последовательности Фибоначчи: 1, 1, 2, 3, 5, 8, 13… найдены. Используя исходную ориентацию, следует заштриховать все нечётные числа, и получится изображение, похожее на знаменитый фрактальный треугольник Серпинского.
Возможно, самое интересное соотношение, найденное в треугольнике — это то, как можно использовать его для поиска комбинаторных чисел, поскольку его первые шесть строк написаны с помощью комбинаторной записи. Поэтому, если нужно рассчитать 4, стоит выбрать 2, затем максимально внимательно посмотреть на пятую строку, третью запись (поскольку счёт с нуля), и будет найден ответ.
Видео:Математические секреты треугольника ПаскаляСкачать

Действия с биномами
Например, есть бином (x + y), и стоит задача повысить его до степени, такой как 2 или 3. Обычно нужно пройти долгий процесс умножения (x + y)² = (x + y)(x + y) и т. д. Если воспользоваться треугольником, решение будет найдено гораздо быстрее. К примеру, нужно расширить (x + y)³. Поскольку следует повышать (x + y) до третьей степени, то необходимо использовать значения в четвёртом ряду фигуры Паскаля (в качестве коэффициентов расширения). Затем заполнить значения x и y. Получится следующее: 1 x³ + 3 x²y + 3 xy² + 1 y³. Степень каждого члена соответствует степени, до которой возводится (x + y).
В виде более удобной формулы этот процесс представлен в теореме бинома. Как известно, всё лучше разбирать на примерах. Итак — (2x – 3)³. Пусть x будет первым слагаемым, а y — вторым. Тогда x = 2x, y = –3, n = 3 и k — целые числа от 0 до n = 3, в этом случае k = . Следует внести эти значения в формулу. Затем заполнить значения для k, которое имеет 4 разные версии, их нужно сложить вместе. Лучше упростить условия с показателями от нуля до единицы.
Как известно, комбинаторные числа взяты из треугольника, поэтому можно просто найти четвёртую строку и подставить в значения 1, 3, 3, 1 соответственно, используя соответствующие цифры Паскаля 1, 3, 3, 1. Последнее — необходимо завершить умножение и упрощение, в итоге должно получиться: 8 x³ — 36 x² + 54x — 27. С помощью этой теоремы можно расширить любой бином до любой степени, не тратя время на умножение.
Биномиальное распределение описывает распределение вероятностей на основе экспериментов, которые можно разделить на группы с двумя возможными исходами. Самый классический пример этого — бросание монеты. Например, есть задача выбросить «решку» — успех с вероятностью p. Тогда выпадение «орла» является случаем «неудачи» и имеет вероятность дополнения 1 – p.
Если спроектировать этот эксперимент с тремя испытаниями, с условием, что нужно узнать вероятность выпадения «решки», можно использовать функцию вероятности массы (pmf) для биномиального распределения, где n — это количество испытаний, а k — это число успехов. Предполагаемая вероятность удачи — 0,5 (р = 0,5). Самое время обратиться к треугольнику, используя комбинаторные числа: 1, 3, 3, 1. Вероятность получить ноль или три «решки» составляет 12,5%, в то время как переворот монеты один или два раза на сторону «орла» — 37,5%. Вот так математика может применяться в жизни.
Видео:Числа сочетаний. Треугольник Паскаля | Ботай со мной #059 | Борис Трушин |Скачать

Зачем нужен треугольник паскаля
- Главная
- Список секций
- Математика
- Треугольник Паскаля
Видео:Числа Фибоначчи и треугольник ПаскаляСкачать

Треугольник Паскаля
Автор работы награжден дипломом победителя III степени
Замечательная геометрическая фигура и самая популярная в школьной программе геометрии — это треугольник. Но треугольники «поселились» не только на страницах учебника геометрии. В данной работе мы рассмотрим не обычный треугольник, а треугольник, состоящий из чисел – треугольник Паскаля, его свойства, связь с числами Фибоначчи и биномиальными коэффициентами.
Познакомиться с таким математическим объектом, как треугольник Паскаля
Пополнить запас научных знаний.
Продолжить знакомство с основными историческими этапами возникновения и развития математической науки, судьбами открытий, именами людей, творивших науку. В первую очередь с биографией ученого Блеза Паскаля.
Самостоятельно попытаться составить данный треугольник.
Рассмотреть свойства треугольника Паскаля.
Определить значимость открытия треугольника Паскаля.
Сформулировать вывод и итоги исследования.
Треугольник Паскаля обладает рядом замечательных свойств, поэтому и носит имя одного из выдающихся людей.
Актуальность данной работы не вызывает сомнения, поскольку обусловлена, с одной стороны большим интересом к теме «Треугольник Паскаля» в современной науке, с другой стороны, её недостаточной разработанностью.
Навыки решения задач с применением треугольника Паскаля помогут в рамках изучения школьного курса математики, при решении олимпиадных задач.
Сбор первоначальных сведений о треугольнике в энциклопедической и учебно-научной литературе.
Построение треугольник Паскаля.
Выявление «волшебных» свойств чисел треугольника.
Изучение возможностей применения треугольника Паскаля.
Формулирование итогов и выводов.
аналитико-статистическая работа со справочной, научно-познавательной и специальной литературой;
поиск информации в интернет — ресурсах.
1.Биография Блеза Паскаля
Прогресс человечества во многом связан с открытиями, сделанными гениями.
Одним из них является Блез Паскаль — французский математик, физик, философ и мастер прозы.
Родился Блез Паскаль в 1623 г. 19 июня в Клермон — Ферране, в семье председателя суда города Этьена Паскаля.
Род Паскалей отличали незаурядные способности, а Блеза одаренность посетила с раннего детства. Этьен Паскаль уделил много внимания развитию умственных способностей сына и уже в 16 лет Блез сочинил труд под названием «Опыт о конических сечениях» в котором содержалась теорема известная, как теорема Паскаля.
Вклад Паскаля в науках очень велик. Вот лишь некоторые из них: заложил основы современной теории вероятностей и математического анализа, сформулировал основной закон гидростатики, написал множество трудов по философии, изобрел шприц, создал гидравлический пресс и вычислительное устройство «Паскалин» (прототип калькулятора), изобрел тачку, придумал омнибус — конные экипажи с фиксированными маршрутами, ставшие впоследствии первым видом регулярного общественного транспорта и пр.
Умер Блез Паскаль 19 августа 1662 года.
Вследствие его больших вкладов в изучение давления в физике, в честь Паскаля назвали единицу измерения давления (Па). Так же в честь Паскаля назвали язык программирования Pascal .
2.Определение и основные свойства треугольника Паскаля.
2.1 История треугольника.
Треугольник Паскаля был известен задолго до 1653 года — даты выхода «Трактата об арифметическом треугольнике» Блеза Паскаля
Похожий треугольник представлен в качестве иллюстрации в книге китайского математика Яна Хуэя, изданной в 1303 году.
О его свойствах было известно также и замечательному персидскому поэту и философу Омару Хайяму еще в начале 12 века. Причем считается, что он познакомился с ним из трактатов арабских и индийских ученых, написанных ранее.
2.2 Построение треугольника Паскаля.
«Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В то же время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике» (Мартин Гарднер).
Треугольником Паскаля называется бесконечная треугольная таблица, в которой (рис.1):
на вершине и по боковым сторонам стоят единицы,
-каждое из остальных чисел равно сумме двух чисел, стоящих над ним в предшествующей строке.
Если очертить треугольник Паскаля, то получится равнобедренный треугольник. Продолжать треугольник можно бесконечно.
2.3 Основные свойства треугольника Паскаля.
Для любой строки под номером n (n = 0, 1, 2…) верно:
Первое и последнее числа – 1; второе и предпоследнее – n.
Строки треугольника симметричны относительно вертикальной оси треугольника.
Сумма чисел n-й строки треугольника Паскаля равна (рис.2)
Первая диагональ — это натуральные числа, идущие по порядку (рис.3).
Вторая диагональ — это «треугольные» числа (Рис.3). Треугольные числа в самом обычном и привычном нам виде показывают, сколько касающихся кружков можно расположить в виде треугольника — как классический пример начальная расстановка шаров в бильярде.
Третья диагональ — это «пирамидальные» числа (один шар мы можем положить на три — итого четыре, под три подложим шесть — итого десять, и так далее) (рис.4).
Четвертая диагональ – это «фигурные числа» в четырехмерном измерении. Это можно представить только в виртуальном мире. Один шар касается четырех, а те, в свою очередь, десяти…
Каждое число треугольника Паскаля равно сумме чисел предыдущей диагонали, стоящей над этим числом.
В каждой строке сумма чисел на нечётных местах равна сумме чисел на чётных местах.
Если номер строки – простое число, то все числа этой строки, кроме 1, делятся на это число.
Каждое число, уменьшенное на 1, равно сумме всех чисел, заполняющих параллелограмм, ограниченный правыми и левыми диагоналями, на пересечении которых стоит это число.
Бином Ньютона – возведение выражения (a + b) в степень. При возведении в степень получаются коэффициенты, равные числам в треугольнике Паскаля.
Сумма чисел n-й восходящей диагонали, проведенной через строку треугольника с номером n − 1, есть n-е число Фибоначчи (число равно сумме двух предыдущих чисел) (рис.5).
Если нечётное число в треугольнике Паскаля заменить на точки контрастного цвета, а чётные — белого цвета, то треугольник Паскаля разобьётся на более мелкие треугольники, образующие изящный узор. Удивительное свойство треугольника Паскаля.
3. Применение треугольника Паскаля.
Где же применяется треугольник Паскаля?
При решении комбинаторных задач.
Треугольник Паскаля используется для решения различных задач в области физики:
принцип минимума потенциальной энергии;
материальные точки и центр тяжести;
центр тяжести системы двух материальных точек;
центр тяжести стержня с многими грузами;
невозможность вечного двигателя.
С появлением вычислительных машин построение треугольника Паскаля стало излюбленной задачкой для начинающих при изучении основ программирования.
Вот далеко не полный перечень свойств чисел треугольника Паскаля и его многочисленных применений.
4. Применение свойств треугольника Паскаля в решении математических задач.
Свойства треугольника Паскаля, наверное, были бы не столь значимы, если бы на их основе нельзя было решать математические задачи. Такие задачи можно встреть в ОГЭ, ЕГЭ и в олимпиадных задачах старшего школьного уровня. Треугольник Паскаля используется при решении комбинаторных задач, для решения различных задач в области физики. С построением вычислительных машин построение треугольника Паскаля стало излюбленной задачкой для начинающих при изучении программирования.
Найдите сумму первых 8 треугольных чисел.
Найдем сумму первых восьми чисел 3 диагонали треугольника Паскаля. (рис.6) Получится 120.
Вася построил из шариков пирамиду. Известно, что на её строительство ушло 286 шариков, сколько «этажей» в Васиной пирамиде?
В данной задаче нам известно, что на строительство пирамиды ушло 286 шариков. Найдем решение с помощью треугольника Паскаля, в котором количество прямоугольников, пересеченных зеленой линией, будет наш ответ. (рис. 7)
Ответ: 11 «этажей».
В магазине «Теплица» продается 6 различных сортов помидор. Сколькими способами можно выбрать из них 3 сорта помидор?
В данной задаче нам даны различные сорта, поэтому повторений не будет и порядок выбора сортов нам неважен, нам важно количество, а именно 3. Найдем решение с помощью нашего треугольника Паскаля, в котором пересечении 3-й диагонали и 6 строки будет наш ответ (рис.8).
На плоскости даны 11 точек, из которых никакие три не лежат на одной прямой и никакие четыре не лежат на одной окружности. Сколько существует окружностей, каждая из которых проходит через три данные точки
Ответ находится на пересечении 11 ряда и 3 диагонали: Это число – 165 (рис.9).
Ответ: 165 окружностей.
Танк может двигаться по квадратам, видимым на карте, размером 4 на 4 только вправо или вниз. Он стоит в точке А. Из штаба пришло задание прибыть в точку В. Сколько маршрутов передвижения может использовать экипаж?
В квадраты a2, a3, a4, а1, b1, c1, d1 танк попадёт 1 способом, в квадрат b2 может добраться 2 способами (рис.10(а)). В квадрат с2 и b3 — 3 способами, d2 и b4 — 4 способами, в c3 – 6 способами, d3, c4 – 10 способами и в квадрат d4 (точка В) – 20 способами. (рис.10(б))
Ответ: 20 способов.
Решив задачу, мы замечаем, что полученные на «карте» числа образуют треугольник Паскаля. Таким образом, можно сделать вывод, что число в треугольнике Паскаля показывает количество способов передвижения от вершины треугольника до данного числа.
Из пункта А по сети дорог идет группа из человек. На каждом перекрестке, начиная с А, пришедшие туда люди делятся пополам – половина идет по направлению l, половина – по направлению m (рис.11). Сколько человек придет в пункты В, С, D, …, I соответственно?
Количество людей, пришедших в искомые точки соответствует числам n-ой строки. В данном случае, n = 7, следовательно¸ искомое количество людей на каждом перекрестке соответствует 7 строке треугольника Паскаля (рис.12).
Ответ: 1, 7, 21, 35, 35, 21, 7, 1.
Возведите в степень: (u — v) 5
У нас есть (a + b) n , где a = u, b = -v, и n = 5. Мы используем 5-й ряд треугольника Паскаля:
Тогда у нас есть:
( u — v ) 5 = ( u + (- v )) 5 = 1( u ) 5 + 5( u ) 4 (- v ) 1 + 10( u ) 3 (- v ) 2 + 10( u ) 2 (- v ) 3 + 5( u ) (- v ) 4 +1(- v ) 5 = u 5 — 5 u 4 v + 10 u 3 v 2 — 10 u 2 v 3 + 5 uv 4 — v 5 .
В ходе исследования мы убедились, что треугольник Паскаля, несмотря на кажущуюся простоту, действительно обладает рядом замечательных свойств, знание которых будет полезно. Этот треугольник широко используется в математике для решения различных видов задач. Треугольник Паскаля имеет применение не только в математике, но и в физике, информатике.
Изучение темы «Треугольник Паскаля» оказалось очень интересной и необычной. Работа над проектом показала, что математика – это не только точная, но и красивая наука.
Гиндикин, С.Г. Рассказы о физиках и математиках/ С.Г.Гиндикин. – М.: Терра, 2013. – 480с.
Энциклопедия для детей Аванта+: В 57 т. Т. 11. Математика/ под ред. М. Аксёновой, В. Володина, М. Самсоновф – М.: Аванта+, 2003. — 688 с.
Корбалан, Ф. Мир математики: В 40 т. Т.1. Золотое сечение, математический язык красоты/ Пер. с исп. — М.: DeAgostini, 2014. — 164 с.: ил.
Гарднер, М. Математические новеллы. (Mathematics Games) / Пер. с англ. Ю.А.Данилова; под ред. Я.А. Смородинского — М.: Мир, 1974. — 456 с.
Успенский, В.А. Треугольник Паскаля. Популярные лекции по математике. Выпуск 43/ ред. В.В. Донченко — 2-е изд. доп. — М.: Наука, 1979. — 48 с.: ил.
📺 Видео
Для чего нужен треугольник Паскаля и как его построить #егэ #математика #shortsСкачать

🔢 Треугольник Паскаля #математика #алгебраСкачать

Основное применение треугольника Паскаля! #shortsСкачать

Математика это не ИсламСкачать

Треугольник ПаскаляСкачать

Как треугольник Паскаля поможет умножать без калькулятораСкачать

РАЗБИРАЕМСЯ С ТРЕУГОЛЬНИКОМ ПАСКАЛЯ ЧАСТЬ II 😊 #shorts #математика #егэ #задачи #егэ2022 #огэ2022Скачать

От треугольника Паскаля к Фракталу Серпинского. Или зачем программисту нужен кругозор?Скачать

Применение треугольника Паскаля #shortsСкачать

#26. Треугольник Паскаля как пример работы вложенных циклов | Python для начинающихСкачать

Полезные мелочи | треугольник ПаскаляСкачать