Общие касательные к двум окружностям
 Взаимное расположение двух окружностей Взаимное расположение двух окружностей |
 Общие касательные к двум окружностям Общие касательные к двум окружностям |
 Формулы для длин общих касательных и общей хорды Формулы для длин общих касательных и общей хорды |
 Доказательства формул для длин общих касательных и общей хорды Доказательства формул для длин общих касательных и общей хорды |
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- Взаимное расположение окружностей
- Окружность
- Основные термины
- Касательная
- Свойства касательной
- Хорда
- Свойства хорд
- Свойства окружности
- Теорема о касательной и секущей
- Теорема о секущих
- Углы в окружности
- Свойства углов, связанных с окружностью
- Длины и площади
- Вписанные и описанные окружности
- Окружность и треугольник
- Окружность и четырехугольники
- 🔍 Видео
Видео:Геометрия 9 класс (Урок№10 - Взаимное расположение двух окружностей.)Скачать

Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  | |
| Каждая из окружностей лежит вне другой |  | |
| Внешнее касание двух окружностей |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  |  |
| Каждая из окружностей лежит вне другой | ||
 | ||
| Внешнее касание двух окружностей | ||
 | ||
| Внутреннее касание двух окружностей | ||
 | ||
| Окружности пересекаются в двух точках | ||
 | ||
 | ||
| Каждая из окружностей лежит вне другой | ||
 Расстояние между центрами окружностей больше суммы их радиусов | ||
| Внешнее касание двух окружностей | ||
 Расстояние между центрами окружностей равно сумме их радиусов | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
 Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой | ||
| Внутренняя касательная к двум окружностям |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  | |
| Внешнее касание двух окружностей |  | |
 | ||
 | ||
| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
 | |
| Внутреннее касание двух окружностей | |
 | |
| Окружности пересекаются в двух точках | |
 | |
| Внешнее касание двух окружностей | |
 | |
 | |
| Каждая из окружностей лежит вне другой | |
 | |
| Внешняя касательная к двум окружностям | |||||||||||||||||||||
| Внутренняя касательная к двум окружностям | |||||||||||||||||||||
| Внутреннее касание двух окружностей | |||||||||||||||||||||
| Окружности пересекаются в двух точках | |||||||||||||||||||||
| Внешнее касание двух окружностей | |||||||||||||||||||||
| Каждая из окружностей лежит вне другой | |||||||||||||||||||||
| Фигура | Рисунок | Формула | ||||||||||||
| Внешняя касательная к двум окружностям |  | |||||||||||||
| Внутренняя касательная к двум окружностям |  | |||||||||||||
| Общая хорда двух пересекающихся окружностей |  | |||||||||||||
| Внешняя касательная к двум окружностям | ||||
 | ||||
| Внутренняя касательная к двум окружностям | ||||
 | ||||
| Общая хорда двух пересекающихся окружностей | ||||
 | ||||
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
 Длина общей хорды двух окружностей вычисляется по формуле Видео:Взаимное расположение окружностей. 7 класс.Скачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Урок 47. Взаимное расположение окружностей (8 класс)Скачать  Взаимное расположение окружностейВыясним, каким может быть взаимное расположение двух окружностей. Две окружности могут пересекаться, не пересекаться либо касаться друг друга. I. Пересекающиеся окружности имеют две общие точки. Расстояние между центрами двух пересекающихся окружностей больше разности, но меньше суммы их радиусов: II. Не пересекающиеся окружности не имеет общих точек. Если одна окружность лежит внутри другой, то расстояние между центрами меньше разности их радиусов:
III. Касающиеся окружности имеют одну общую точку — точку касания. При внешнем касании расстояние между центрами окружностей равно сумме их радиусов: При внутреннем касании расстояние между центрами равно разности радиусов: Концентрические окружности разного радиуса не пересекаются. Расстояние между центрами концентрических окружностей равно нулю: O1O2=0. ОкружностьОкружностью называется фигура, состоящая из всех точек плоскости, находящихся от данной точки на данном расстоянии. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности. Часть плоскости, ограниченная окружностью называется кругом. Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Сегментом называется часть круга, ограниченная дугой и стягивающей ее хордой. Видео:Взаимное расположение окружности и прямой. 7 класс.Скачать  Основные терминыКасательнаяПрямая, имеющая с только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Свойства касательной
Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. ХордаОтрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром. Свойства хорд
Дуги, заключенные между параллельными хордами, равны. Если две хорды окружности, AB и CD пересекаются в точке M , то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD. Видео:Взаимное расположение окружностей. Практическая часть. 7 класс.Скачать  Свойства окружности
Теорема о касательной и секущейЕсли из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC 2 = MA•MB . Теорема о секущихЕсли из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть. MA•MB = MC•MD. Видео:8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать  Углы в окружностиЦентральным углом в окружности называется плоский угол с вершиной в ее центре. Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом. Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. Мерой дуги может служить мера соответствующего ей центрального угла. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром. Свойства углов, связанных с окружностью
Углы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны. Вписанный угол, опирающийся на диаметр, равен 90°. Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами. Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать  Длины и площади
Площадь S круга радиуса R вычисляется по формуле: Длина дуги окружности L радиуса R с центральным углом ,измеренным в радианах, вычисляется по формуле: Площадь S сектора радиуса R с центральным углом в радиан вычисляется по формуле: Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать  Вписанные и описанные окружностиОкружность и треугольник
где S — площадь треугольника, а — полупериметр; центр описанной окружности — точка пересечения серединных перпендикуляров, ее радиус R вычисляется по формуле: здесь a, b, c — стороны треугольника, — угол, лежащий против стороны a , S — площадь треугольника; Окружность и четырехугольники
в четырехугольник можно вписать окружность тогда и только тогда, когда у него равны суммы противоположных сторон:
🔍 ВидеоВзаимное расположение двух окружностей. Урок 8. Геометрия 9 классСкачать  Взаимное расположение прямой и окружности | Геометрия 7-9 класс #68 | ИнфоурокСкачать  Геометрия 8 класс (Урок№25 - Взаимное расположение прямой и окружности.)Скачать  Урок по геометрии ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ОКРУЖНОСТИСкачать  Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать  Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  Взаимное расположение окружностейСкачать  Взаимное расположение двух окружностей.Использование уравнений окружности и прямой при решении задачСкачать  Тема 26. Взаимное расположение окружностейСкачать  Геометрия 16-09. Взаимное расположение двух и более окружностей. Задача 9Скачать  Взаимное расположение двух окружностейСкачать  |




























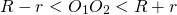


 Если одна окружность находится вне другой, расстояние между центрами больше суммы их радиусов:
Если одна окружность находится вне другой, расстояние между центрами больше суммы их радиусов: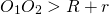 R + r]» title=»Rendered by QuickLaTeX.com»/>
R + r]» title=»Rendered by QuickLaTeX.com»/>