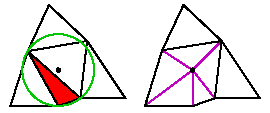Вытянутый треугольник как называется фигура (7 видео)

Геометрические объемные фигуры и их названия: шар, куб, пирамида, призма, тетраэдр

Геометрические объемные фигуры — это твердые тела, которые занимают ненулевой объем в евклидовом (трехмерном) пространстве. Эти фигуры изучает раздел математики, который носит название «пространственная геометрия». Знания о свойствах объемных фигур применяются в инженерии и в науках о природе. Рассмотрим в статье вопрос, геометрические объемные фигуры и их названия.

Содержание

Геометрические объемные тела
Фигура куб: описание
Фигура пирамида
Фигура тетраэдр: описание
Фигура призма
Фигура шар
Треугольник объемный название
Названия геометрических фигур в картинках (23 ФОТО)
Какие бывают геометрические фигуры?
треугольник в объеме — Как называется объемный треугольник. Вот квадрат — кубом, а треугольник — ? — 22 ответа
Виды треугольников
Вытянутый треугольник как называется фигура
Правильная геометрия фигуры
Очень вытянутые треугольники с удаленным центром.
Малые углы между гранями.
💡 Видео

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Геометрические объемные тела

Поскольку эти тела имеют конечную размерность в трех пространственных направлениях, то для их описания в геометрии используют систему из трех координатных осей. Эти оси обладают следующими свойствами:

Они ортогональны друг другу, то есть перпендикулярны.
Эти оси нормализированы, то есть базисные вектора каждой оси имеют одинаковую длину.
Любая из осей координат — это результат векторного произведения двух других.

Говоря о геометрических объемных фигурах и их названиях, следует отметить, что все они принадлежат к одному из 2-х больших классов:

Класс полиэдров. Эти фигуры, исходя из названия класса, имеют прямые ребра и плоские грани. Грань — это плоскость, которая ограничивает фигуру. Место соединения двух граней называется ребром, а точка соединения трех граней — это вершина. К полиэдрам относятся геометрическая фигура куб, тетраэдры, призмы, пирамиды. Для этих фигур справедлива теорема Эйлера, которая устанавливает связь между числом сторон (С), ребер (Р) и вершин (В) для каждого полиэдра. Математически эта теорема записывается так: С + В = Р + 2.
Класс круглых тел или тел вращения. Эти фигуры имеют хотя бы одну поверхность, образующую их, изогнутой формы. Например, шар, конус, цилиндр, тор.

Что касается свойств объемных фигур, то следует выделить два самых важных из них:

Наличие определенного объема, который фигура занимает в пространстве.
Наличие у каждой объемной фигуры площади поверхности.

Оба свойства для каждой фигуры описываются конкретными математическими формулами.

Рассмотрим ниже самые простые геометрические объемные фигуры и их названия: куб, пирамиду, призму, тетраэдр и шар.

Видео:Тип фигуры «ПЕРЕВЁРНУТЫЙ ТРЕУГОЛЬНИК» // Способы коррекцииСкачать

Фигура куб: описание

Под геометрической фигурой куб понимают объемное тело, которое образовано 6-тью квадратными плоскостями или поверхностями. Также эту фигуру называют правильный гексаэдр, поскольку она имеет 6 сторон, или прямоугольный параллелепипед, так как он состоит из 3-х пар параллельных сторон, которые взаимно перпендикулярны друг другу. Называют куб и прямоугольной призмой, у которой основание является квадратом, а высота равна стороне основания.

Поскольку куб является многогранником или полиэдром, то для него можно применить теорему Эйлера, чтобы определить число его ребер. Зная, что число сторон равно 6, а вершин у куба 8, число ребер равно: Р = С + В — 2 = 6 + 8 — 2 = 12.

Если обозначить буквой «a» длину стороны куба, тогда формулы для его объема и площади поверхности будут иметь вид: V = a 3 и S = 6*a 2 , соответственно.

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Фигура пирамида

Пирамида — это полиэдр, который состоит из простого многогранника (основание пирамиды) и треугольников, которые соединяются с основанием и имеют одну общую вершину (вершина пирамиды). Треугольники называются боковыми гранями пирамиды.

Геометрические характеристики пирамиды зависят от того, какой многоугольник лежит в ее основании, а также от того, является ли пирамида прямой или косой. Под прямой пирамидой понимают такую пирамиду, для которой перпендикулярная основанию прямая, проведенная через вершину пирамиды, пересекает основание в ее геометрическом центре.

Одной из простых пирамид является четырехугольная прямая пирамида, в основании которой лежит квадрат со стороной «a», высота этой пирамиды «h». Для этой фигуры пирамиды объем и площадь поверхности будут равны: V = a 2 *h/3 и S = 2*a*√(h 2 +a 2 /4) + a 2 , соответственно. Применяя теорему Эйлера для нее, с учетом того, что число граней равно 5, и число вершин равно 5, получаем количество ребер: Р = 5 + 5 — 2 = 8.

Видео:ТИП ФИГУРЫ. КАК ТОЧНО ОПРЕДЕЛИТЬ СВОЙ ТИП ФИГУРЫ?Скачать

Фигура тетраэдр: описание

Под геометрической фигурой тетраэдр понимают объемное тело, образованное 4-мя гранями. Исходя из свойств пространства, такие грани могут представлять только треугольники. Таким образом, тетраэдр является частным случаем пирамиды, у которой в основании лежит треугольник.

Если все 4-ре треугольника, образующие грани тетраэдра, являются равносторонними и равными между собой, то такой тетраэдр называется правильным. Этот тетраэдр имеет 4 грани и 4 вершины, число ребер составляет 4 + 4 — 2 = 6. Применяя стандартные формулы из плоской геометрии для рассматриваемой фигуры, получаем: V = a 3 * √2/12 и S = √3*a 2 , где a — длина стороны равностороннего треугольника.

Интересно отметить, что в природе некоторые молекулы имеют форму правильного тетраэдра. Например, молекула метана CH₄, в которой атомы водорода расположены в вершинах тетраэдра, и соединены с атомом углерода ковалентными химическими связями. Атом углерода находится в геометрическом центре тетраэдра.

Простая в изготовлении форма фигуры тетраэдр используется также в инженерии. Например, тетраэдрическую форму используют при изготовлении якорей для кораблей. Отметим, что космический зонд НАСА, Mars Pathfinder, который совершил посадку на поверхность Марса 4 июля 1997 года, также имел форму тетраэдра.

Видео:Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Фигура призма

Эту геометрическую фигуру можно получить, если взять два многогранника, расположить их параллельно друг другу в разных плоскостях пространства, и соединить их вершины соответствующим образом между собой. В итоге получится призма, два многогранника называются ее основаниями, а поверхности, соединяющие эти многогранники, будут иметь форму параллелограммов. Призма называется прямой, если ее боковые стороны (параллелограммы) являются прямоугольниками.

Призма — это полиэдр, поэтому для нее верна теорема Эйлера. Например, если в основании призмы лежит шестиугольник, тогда, количество сторон у призмы равно 8, а количество вершин — 12. Число ребер будет равно: Р = 8 + 12 — 2 = 18. Для прямой призмы высотой h, в основании которой лежит правильный шестиугольник со стороной a, объем равен: V = a 2 *h*√3/4, площадь поверхности равна: S = 3*a*(a*√3 + 2*h).

Видео:Типы Фигур: ПЕРЕВЕРНУТЫЙ ТРЕУГОЛЬНИК. Советы и упражненияСкачать

Фигура шар

Говоря о простых геометрических объемных фигурах и их названиях, следует упомянуть шар. Под объемным телом под названием шар понимают тело, которое ограничено сферой. В свою очередь, сфера — это совокупность точек пространства, равноудаленных от одной точки, которая называется центром сферы.

Поскольку шар относится к классу круглых тел, то для него не существует понятия о сторонах, ребрах и вершинах. Площадь поверхности сферы, ограничивающей шар, находится по формуле: S = 4*pi*r 2 , а объем шара можно вычислить по формуле: V = 4*pi*r 3 /3, где pi — число пи (3,14), r — радиус сферы (шара).

Видео:песня формы | геометрические фигуры для детей | типы фигур | учить формы | Shape SongСкачать

Треугольник объемный название

Видео:Треугольник - 3 точки?Скачать

Названия геометрических фигур в картинках (23 ФОТО)

Геометрия как наука началась с древних греков. Они подстмотрели у египтян землемерные работы и оформили это в виде аксиом и правил. Первым научным трудом в этой области был «Начала» Евклида.

Объёмные геометрические фигуры

Названия объёмных фигур на английском

Синие фигуры с английскими названиями

Синие фигуры с русскими названиями

Разноцветные фигуры с английскими названиями

Простые фигуры кубической сингонии

Куб, икосаэдр, тетраэдр, октаэдр, додекаэдр

Весёлые геометрические фигуры

Треугольник, пятиугольник, шестиугольник, семиугольник, восьмиугольник

Видео:Как найти периметр данной фигуры? Решение за одну минуту!Скачать

Какие бывают геометрические фигуры?

В сферу изучения науки геометрии входят плоские (двухмерные) фигуры и объмные фигуры (трхмерные).

Их изучает планиметрия. Точка тоже плоская фигура.

Из объмных известны:

Их изучает стереометрия.

Двухмерные фигуры — треугольник, квадрат, прямоугольник, ромб, трапеция, параллелограмм, круг, овал, эллипс, многоугольники (пентагон, гексагон, гептагон, октагон и другие).

К фигурам также относится и точка.

Трехмерные фигуры — куб, сфера, полусфера, конус, цилиндр, пирамида, параллелепипед, призма, эллипсоид, купол, тетраэдры и множество других, выходящие из вышеуказанных. Далее идут очень сложные геометрические фигуры — различные многогранники, которые по сути могут содержать бесконечное количество граней. Например, большая клинокорона — состоит из 2-х квадратов и 16-ти правильных треугольников или клинокорона, составленная из 14 граней: 2 квадрата и 12 правильных треугольника.

Говоря о геометрических фигурах, можно выделить такие две закономерные группы как:

1) Двухмерные фигуры;

2) И трхмерные фигуры.

Итак, поподробнее о двухмерным, к ним можно отнести такие фигуры как:

А вот что касается трхмерных фигур, то вот какими они могут быть:

Очертания фигур и все возможные действия с ними изучают математические науки геометрия (изучает плоские фигуры) и стереометрия (предмет изучения — объемные фигуры). Я в школе любила и ту, и другую науку.

Вот так классифицируются плоские (2D) фигуры:

С тремя сторонами — это треугольник. С четырьмя сторонами — это квадрат, ромб, прямоугольник, трапеция. А еще может быть параллелограмм и окружность (овал, круг, полукруг, эллипс).

Объемные фигуры (3D) классифицируются таким образом:

Это куб, параллелепипед, тетраэдр, цилиндр, пирамида, икосаэдр, шар, додекаэдр, конус, октаэдр, призма, сфера. К тому же есть усеченные фигуры (пирамида, конус). В зависимости от основания, пирамида, призма делятся на треугольные, четырехгранные и так далее.

Детские игрушки (пирамидки, мозаика и другие) позволяют с раннего детства знакомить детей с геометрическими объемными фигурами. А плоские фигуры можно нарисовать и вырезать из бумаги.

Из двухмерных можно назвать следующие:

круг;
овал;
квадрат;
прямоугольник;
параллелограмм;
трапеция;
пятиугольник (шестиугольник и т.д.);
ромб;
треугольник.

С трехмерными немного посложнее:

куб;
цилиндр;
конус;
призма;
сфера или шар;
параллелепипед;
пирамида;
тетраэдр;
икосаэдр;
октаэдр;
додекаэдр.

Думаю многие, прочитав последния названия, спросили про себя: quot;Что-что?quot;. Для наглядности — иллюстрация:

На самом деле фигур в математике достаточно. Плоские фигуры это — прямоугольники, квадрат, треугольник, пятиугольник, шестиугольник, круг. Объемные фигуры или 3D фигуры — это как пирамида, так и куб и додекаэдр, и тд.

1 Из двухмерных фигур:

круг, треугольник, квадрат, ромб, прямоугольник, трапеция, параллелограмм, овал и многоугольник. Ещ звезда (пентаграмма), если е можно называть фигурой.

2 Из трхмерных фигур:

Призма, пирамида, параллелепипед, призма, шар (сфера), цилиндр, полусфера (половинка от сферы, то есть шар, разрезанный пополам) и конус. Пирамиды делятся на треугольные, четырхугольные и так далее (почти до бесконечности). Чем больше у пирамиды углов в основании, тем больше она напоминает конус.

Двухмерные фигуры (2D): угол; многоугольник (разновидности многоугольников: треугольник, четырхугольник разновидности четырхугольника: параллелограмм, прямоугольник, ромб, квадрат, трапеция, дельтоид, пятиугольник, шестиугольник и т. д. до бесконечности); окружность, круг, круговой сегмент, круговой сектор, эллипс, овал.

Трхмерные фигуры (3D): двугранный угол, многогранный угол; многогранник (разновидности многогранников: призма разновидности призмы: параллелепипед, куб, антипризма, пирамида разновидность тетраэдр, усечнная пирамида, бипирамида разновидность октаэдр, додекаэдр, икосаэдр, клин, обелиск); цилиндр, усечнный цилиндр, отрезок цилиндра (он же цилиндрическая подковка или quot;копытоquot;), конус, усечнный конус, сфера, шар, шаровой сегмент, шаровой слой, шаровой сектор, эллипсоид, геоид.

С самого начала мы на уроках геометрии изучаем простые фигуры, которые являются плоскими, то есть располагаются на одной плоскости.

Далее, перед нами открывается мир объмных фигур, которые необходимо представлять и понимать, как они расположены и как грамотно их нарисовать, чтобы было понятно не только вам, но и окружающим.

Итак, перечень основных фигур можно изучить ниже.

В последнее время мне как раз приходилось рассказывать своим внучкам и внуку, какими могут быть геометрические фигуры.

Начинали с плоских фигурок, вырезанных из картона или сделанные из пластмассы, дети учились различать треугольник и квадрат, овал и круг, прямоугольник, ромб и многоугольник.

Помогали в запоминании названий фигур и вот такие специальные игрушки с отверстиями определнной формы.

Позднее перешли на объмные фигурки, кубики и конусы, параллелепипеды, шары и кольца, пирамидки и цилиндры.

До школы они пока не доросли, а когда пойдут, то их научат различать равнобедренные и равносторонние треугольники, узнают про луч и точку, про окружность и вс остальное.

Видео:Объемные Геометрические ФИГУРЫ Загадки для ДЕТЕЙСкачать

треугольник в объеме — Как называется объемный треугольник. Вот квадрат — кубом, а треугольник — ? — 22 ответа

В разделе Другое на вопрос Как называется объемный треугольник. Вот квадрат — кубом, а треугольник — ? заданный автором Дарья Попкова лучший ответ это Тетраэдр.

[гуру]пирамидаОтвет от Евровидение[новичек]незнОтвет от Прострочить[новичек]хзОтвет от Обособиться[новичек]ПирамидаОтвет от Ёофья Раскопова[новичек]ПИРАМИДАААА!!

КАКОЙ НА ФИГ ТЭТРАЭДР.

Ответ от сергей беляев[новичек]Так-то у тетраэдра 4 угла, а у пирамиды их 5. Какой и них-зависит от кол-ва углов в основанииОтвет от Денис Рыбкин[активный]Пирамида или тетраэдр. Но гораздо чаще его называют пирамидойОтвет от Артур Татулян[новичек]Разница между пирамидой и тетраэдром в том, что у пирамиды четыре боковые грани в виде треугольников и нижняя грань в виде прямоугольника, а у тетраэдра три боковые грани в виде треугольников и нижняя грань в виде треугольника. По этому грамотнее будет, если сказать, что объемный треугольник — тетраэдр, так как все грани тэтраэдра в виде треугольников!Ответ от сафонов савелий[новичек]ПирамидаОтвет от Golubev Konstantin[новичек]Треугольная ПризмаОтвет от Любовь К[новичек]тэтраздерТреугольник на ВикипедииПосмотрите статью на википедии про ТреугольникТреугольник Рёло на ВикипедииПосмотрите статью на википедии про Треугольник Рёло

Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Виды треугольников

В зависимости от величин углов и соотношения длин сторон различают следующие виды треугольников.

Виды треугольников по углам:

остроугольные
прямоугольные
тупоугольные

Остроугольный треугольник — это треугольник, все углы которого острые (то есть градусная мера каждого угла меньше 90º).

Прямоугольный треугольник — это треугольник, у которого один угол прямой (то есть имеет градусную меру 90º).

Тупоугольный треугольник — это треугольник, у которого один угол — тупой (то есть имеет градусную меру больше 90º).

Виды треугольников по сторонам:

равносторонние
равнобедренные
разносторонние

Равносторонний треугольник (или правильный треугольник) — это треугольник, у которого все три стороны равны.

Равнобедренный треугольник — это треугольник, у которого две стороны равны.

Разносторонний треугольник — треугольник, все стороны которого имеют разную длину.

Если в задаче ничего не сказано о виде треугольника, его считают произвольным, то есть разносторонним.

Отрезки равной длины на чертеже отмечают равным количеством черточек:

Видео:Учим плоские геометрические фигуры с паровозиком Чух-Чухом - часть первая (1). Геометрия для детейСкачать

Вытянутый треугольник как называется фигура

Большинство методов численного расчета основаны на переходе от протяженной задачи к дискретной, т.е. к такой задаче, в которой не находят функции распределения той или иной физической величины, а находят лишь значения этой величины в некотором конечном наборе точек. При этом пространство, параметры которого расчитываются в задаче, разбивается на конечное число элементов, целиком заполняющих это пространство. Элементы, как правило, являются простыми фигурами и для них можно решить задачу. Для простраственной задачи элементы заключают в себе объем, например таким элементом может быть тетраэдр. Для плоских задач, либо пространственных задач, но тем или иным способом сводящихся к плоским, используются различные плоские полигональные фигуры.

Проблема оптимального разбиения пространства задачи является подчас очень сложной. На каждый элемент разбиения могут накладываться довольно жесткие ограничения. К тому же, в пространстве задачи могут быть некие характерные области, где параметры меняются довольно резко. Например, в задачах механики твердого деформируемого тела, такие области образуются вблизи концентраторов напряжений и в них напряжения меняются чрезвычайно резко. Такие области требуют более частого разбиения.

В современных задачах подобного класса разбиение включает в себя огромное количество элементов, как правило не менее тысячи. Создавать вручную такие разбиения не представляется возможным, поэтому в дополнение к основным расчетным алгоритмам должны быть созданы и алгоритмы генерации разбиения.

Расчет тонких плит методом конечных элементов представляет из себя как раз такую задачу. В ней пространственная задача сводится к «псевдоплоской», разбиение производится в плоскости, а толщина является параметром каждого элемента. Для максимальной универсальности и упрощения алгоритма разумно выбрать треугольный конечный элемент — самый простой двумерный элемент. Поэтому сетка будет треугольной. На треугольники сетки накладываются два основных ограничения: треугольник не должен быть слишком вытянутым (skinny triangle), т.е. его минимальный угол ограничен сверху; площадь треугольника не должна превышать определенного значения, ввиду того, что перемещения находятся только в вершинах и центре тяжести треуголька и есть шанс упустить максимальное перемещение (следовательно и напряжение) при достаточно больших элементах.

Таким образом, необходим алгоритм, разбивающий полигональную фигуру. При этом на эту фигуру должно накладываться минимум ограничений: не должно быть никаких ограничений, касающихся выпуклости; она может содержать отверстия, выделенные области (другие физ. характеристики, нагрузки и т.п.). Треугольники получаемой сетки должны удовлетворять двум перечисленным выше требованием. Желательно, чтобы алгоритм был адаптивным и требовал как можно меньшего участия человека. Обзор cуществующих методов

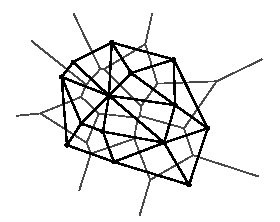
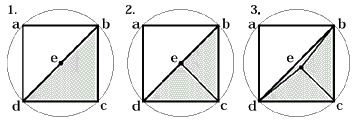
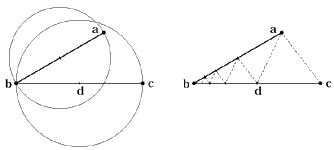
Основными понятиями теории триангуляции и плоских треугольных сеток являются диаграммы Вороного (см. рис. 1) и триангуляция Делоне (Delaunay triangulation см. рис. 1). Диаграммами Воронова на плоскости для множества точек называют системы полигональных фигур, образуемых линиями, перпендикулярными отрезкам, соединяющими соседние точки и проходящим через середины этих отрезков. Триангуляция Делоне на плоскости — это множество не пересекающихся треугольников, в котором ни одна точка, не принадлежащая данному треугольнику не попадает в окружность, описанную вокруг этого треугольника. Все рассматриваемые методы оперируют этими понятиями в том или ином виде. Приведу лишь названия наиболее известных алгоритмов генерации сетки:

Radial sweep algorithm.
Recursive split algorithm (Алгоритм последовательного разбиения).
Divide-and-conquer algorithm (Алгоритм деления-и-включения).
Step-by-step algorithm.
Modified hierarchical algorithm (Модифицированный иерархический алгоритм)
Incremental algorithm.
Incremental delete-and-build algorithm.

Все эти алгоритмы не предназначены непосредственно для генерации конечно-элементной сетки. Они подразумевают наличие опорных точек, которые будут потом узлами сетки. К сетке для метода конечных элементов предъявляется ряд особых требований. Во-первых, треугольники не должны быть сильно вытянутыми, т.к. наличие таких треугольников отрицательно сказывается на точности результатов расчета. Во-вторых, должен быть учтен характер работы конструкции и ее геометрия, т.е. в местах концентрации напряжений сетка должна сгущаться. Все эти требования учтены в алгоритме генерации треугольных иррациональных конечно-элементных сеток Рапперта.
Алгоритм Рапперта

Этот алгоритм довольно новый, он был опубликован в 1994 году. Его разработал Джим Рапперт еще будучи студентом в рамках проекта, поддерживаемым NASA. Алгоритм адаптирован для метода конечных элементов и перечисленные выше требования, предъявляемые к конечно-элементным сеткам удовлетворяются автоматически. К его преимуществам можно отнести и то, что алгоритм легко параметризуется и управляется.

Если говорить точнее, этот алгоритм не является алгоритмом генерации, а лишь алгоритмом улучшения качеств сетки (refinement). В нашем случае входными данными для него будут являться геометрия конструкции в виде замкнутых полигонов и первичное разбиение конструкции на треугольники. Для получения первичного разбиения при реализации алгоритма генерации сетки я использовал упрощенный вариант алгоритма step-by-step (см. п. 5) с использованием в качестве точек вершин полигонов исходной геометрии. В этом пункте, при описании алгоритма, будем считать, что первоначальное разбиение уже создано. Более подробно на генерации первоначального разбиения мы остановимся ниже (см. п. 5).

При описании своего алгоритма Рапперт вводит свою терминологию, мы также будем придерживаться этой терминологии.

Элемент по смыслу совпадает с конечным элементом. Это элементарная часть пространства на множество которых мы хотим разбить более сложную область этого пространства. В нашем случае элементом является треугольник.

Узел (node) — точка в которой сходятся грани и соприкасаются несколько элементов. В отличие от вершин элементов узел общий для всех соприкасающижся в одной точке элементов.

Сегмент (segment) — это отрезок, соединяющий две соседние точки лежащие на границе области разбиения, другими словами этот отрезок принадлежит контурам области.

Грань (edge) — это отрезок по которому граничат два соприкасающихся треугольника. Используя предыдущее определение можно сказать, что все множество отрезков, соединяющих вершины элементов, в любой момент работы алгоритма складывается из сегментов и граней.

Включенная точка (encroached point) — любая вершина текущей сетки, которая находится внутри окружности, радиусом которой является любой сегмент.

«Неправильный треугольник» (bad triangle) — это треугольник неудовлетворяющий глобальным условиям, которые накладываются на генерируемую сетку.

Вытянутый треугольник (skinny triangle) — треугольник, имеющий одну сторону, намного отличающуюся от других двух. То есть треугольник слишком вытянут вдоль некоторой прямой. На критериях «вытянутости» мы остановимся ниже.

Алгоритм опирается на две базовые процедуры: a) разбиение неправильного треугольника с введением нового узла и b) разбиение сегмента, принадлежащего границе области разбиения с введением нового узла. При разбиении треугольника происходит следующее:

Вычисляются координаты центра окружности, описанной вокруг треугольника, подлежащего разбиению.
В эту точку добавляется новый узел.
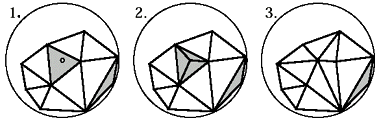
Удаляется треугольник, подлежащий разбиению и прилегающие и добавляются новые, как показано на рисунке 3.

Вторая базовая процедура состоит в следующем:

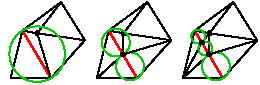
Если в окружность, диаметром которой является сегмент, принадлежащий границе области разбиения попадает точка, не принадлежащая этому сегменту, то сегмент делится на две части.
Удаляется треугольник, которому принадлежал первоначальный сегмент и добавляются два новых треугольника(см. рис. 2).

Принцип работы алгоритма состоит в цикле определения «неправильных» треугольников, т.е. треугольников, не удовлетворяющих определенному критерию, и произведение над ним одной из базовых процедур. В оригинальном алгоритме, предложенным Джимом Раппертом используется один критерий — минимальный угол в треугольниках сетки. В каждом треугольнике сетки определяется минимальный угол и, затем, сравниваются минимальные углы для всех треугольников с целью нахождения минимального угла сетки. Другими словами, минимальный угол в сетке равен минимально возможному углу, образованому двумя сегментами, либо двумя гранями, либо сегментом и гранью, имеющими общий узел.

Для задачи генерации конечно-элементной сетки этого критерия недостаточно, дело в том, что функции, значения которых мы хотим получить в узлах сетки, нелинейны, при этом они могут иметь области с большими значениями своих производных (области концентрации напряжений). При больших размерах конечного элемента, велик риск попросту упустить максимальные значения напряжений, поэтому был введен еще один критерий — условие максимальной площади треугольника. Сочетание этих двух ограничений гарантирует, что в сетке углы всех треугольников не менее значения, заданного пользователем, а площади всех треугольников не более другого значения, также задаваемого пользователем.

Математически доказано, что критерий минимального угла автоматически обеспечивает сгущение сетки вблизи мелких подробностей: отверстий, углов, вырезов, т.е. концентраторов напряжений. А критерий максимальной площади является дополнительным, регулирующим размер треугольников. Введение этого критерия было необходимо для адаптации этого алгоритма к методу конечных элементов. Этот дополнительный критерий снижает «эффективность» получаемого разбиения, т.к. введением этого критерия мы ограничиваем площадь треугольников сверху, тем самым увеличивая количество треугольников в получаемой сетке. Но задав минимальную площадь треугольника достаточно большой, можно сделать так, что фактически будет работать только критерий минимального угла.

Все описаные процедуры выполняются в определенной последовательности, они имеют разный приопитет. Общая схема работы алгоритма следующая:

Производится поиск включенной (encroached) точки перебором всех точек и сегментов (только сегментов, но не граней).
Если такая точка найдена то над сегментом, который включает ее выполняется процедура деления сегмента пополам и производится возврат на шаг 1. Если включенных точек не было найдено, то алгоритм переходит на следующий шаг.
Производится поиск треугольника с минимальным углом.
Если минимальный угол меньше заданного параметра, то над треугольником, его содержащем производится процедура деления и производится возврат на шаг 1. В противном случае происходит переход на следующий шаг.
Производится поиск треугольника максимальной площадью.
Если максимальная площадь больше заданного параметра, то над таким треугольником производится процедура деления и производится возврат на шаг 1. В противном случае происходит переход на следующий шаг.
Все условия удовлетворены. Конец работы алгоритма

Автор в своей работе приводит строгие математические доказательства, гарантирующие правильную работу алгоритма при минимальном угле a
Модификация алгоритма Рапперта

В работе для Journal of Algorithms раскрыт только лишь чисто математический аспект проблемы, хотя вероятней всего алгоритм разрабатывался для решения прикладных задач и для генерации конечно-элементной сетки в том числе. К тому же, и математическая сторона была раскрыта не полностью, а только лишь с точки зрения сходимости и некоторых особенностей. Ряд самых неочевидных подводных камней не поднимается на обсуждение. Видимо это объясняется тем, что это проект NASA и, вероятно, имеет какую-то степень закрытости.

В том варианте, в котором он был предложен автором, алгоритм не обладал хорошей сходимостью и устойчивостью. Опытным путем было установлено, что углы a > 25° были недоступны для него. Для повышения качества работы алгоритма, помимо двух вышеперечисленных процедур была введена еще одна — процедура поворота диагонали. К сожалению автор опустил этот момент и не упомянул о нем, несмотря на то что, ее роль в работе алгоритма очень высока. Эта процедура, на самом деле, неявно присутствует в оригинальном алгоритме Рапперта (см.рис. 2, 3), но все же эту процедуру лучше выделить в отдельную и остановиться на ней подробно. Это упрощает и понимание работы алгоритма, и его программирование. На рисунках видно, что помимо непосредственного добавления новых тругольников, производятся и еще некоторые операции. Эти операции есть ничто иное как смена диагонали.

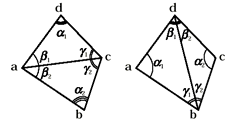
Суть ее заключается в следующем. Два треугольника, имеющие общую грань, образуют четырехугольник, разделенный диагональю. Внутри такого образования диагональ имеет два возможных положения. На рисунке 4 показаны эти положения — отрезки ac и bd. В общей системе триангуляции положение этой диагонали является локальной характеристикой для четырехугольника. Действительно, смена положения, кроме некоторых случаев, обсуждаемых позже, изменит характеристики только этих двух треугольников.

Этой возможностью можно воспользоваться для локального улучшения свойств сетки. Для этого необходимо выяснить еще одно обстоятельство — критерий, который бы давал ответ, улучшится ли локальная характеристика сетки при смене положения диагонали, т.е. дал ответ, надо или не надо производить эту операцию над каждым конкретным четырехугольника.

Вариантов такого критерия можно придумать множество. Но нами было опробовано три варианта: длина диагонали, отношение площадей до и после смены диагонали и все тот же критерий минимального угла. Все эти критерии эмпирические и ни один из них не исследовался теоретически, хотя они и были тщательно испытаны на практике. Но этот список был ограничен лишь в силу того, что автор не ставил себе целью провести исследовательскую работу, было необходимо лишь создать хорошо работающую программу. Поэтому этот список открыт и может пополняться.

К каждому возможному варианту необходимо предъявлять ряд требований. Во-первых, это адекватность этого критерия, т.е. улучшает ли он свойства сетки на самом деле, и если да, то с какими оговорками. Может случится, что способ хорош внешне, прост, не трудоемок, но работет при ряде ограничений. Эти ограничения и могут свести на нет все преимущества предлагаемого метода. Во-вторых, необходимо учитывать машинную трудоемкость выбираемого метода. И в-третьих, эффективность его будет зависеть еще и от сложности алгоритма, реализующего предлагаемый метод.

Первый, возможно самый очевидный критерий — это длина диагонали (см. рис. 4). Действительно, зрительно, диагональ ac кажется гораздо более удачной диагонали bd для минимального угла двух треугольников и поменяв эту диагональ мы, вероятно, добьемся улучшения свойств сетки. У этого способа, к тому же, есть преимущества: он не трудоемок в вычислительном плане и его просто запрограммировать. Но есть у него и критический недостаток — он неадекватен. На рисунке 5 показан случай, где использование критерия минимальной длины диагонали может привести к серьезному ухудшению свойств сетки.

Диагональ bd короче диагонали ac , поэтому, по критерию минимальной длины диагонали, диагональ ac надо поменять на bd . Но это приведет к появлению очень тонкого треугольника, а их появление крайне нежелательно, а часто и вовсе становится критическим. Этот случай уже не так просто формализуется, и запрограммировав его, легко убедиться, что это дополнительное условие сильно «утяжеляет» алгоритм, сводя на нет все его преимущества.

Разумеется, что и на практике, в силу своей неадекватности, ничего хорошего этот критерий не показал и от него пришлось отказаться.

Следующий очевидный критерий можно получить сравнивая минимальные углы в двух треугольниках до и после смены диагонали, для предсказания эффективности этого действия (см. рис. 6). Такой критерий является абсолютно адекватным, т.к. он совпадает с основным глобальным критерием сетки — критерием минимального угла и это его существенное преимущество.

Применение такого критерия действительно кажется заманчивым в силу его объективности, но у него есть один специфический недостаток — трудоемкость. Для него необходимо вычислить 6 углов, а по объему операций трудоемкость этого превосходит более чем в 10 раз вычисление двух длин отрезков. Поэтому было решено попробовать и другое решение.

Действие вычисления площади по трудоемкости сравнимо с нахождением одного угла. Поэтому третьим критерием является сравнение площадей двух треугольников, точнее не сравнение самих площадей, а сравнение с единицей отношения площадей до и после смены диагонали. Сравниваться должна нормализованная величина отношения площадей до и после смены диагонали. Другими словами величина этого отношения дожна быть меньше 1, если она получается больне 1, то сравнивается ее обратная величина. Более близкое к единице значение отношений означает более равномерное распределение площадей. Этот критерий теоретически не обоснован, он больше интуитивный, эмпирический, но тем не менее, на практике работает довольно хорошо.

Но все же, сравнивая качество работы второго и третьего критерия было решено использовать второй. Из-за своего совпадения с глобальным критерием качества сетки он показывает более стабильную работу всего алгоритма в целом.

Выше было упомянуто о существовании исключения, при котором нарушается локальность изменения положения диагонали внутри четырехугольника. На рисунке 7 показан такой случай.

Как видно, новая диагональ выходит за границы кластера, пересекая грани уже существующих соседей. Из-за этого получается пересечение площадей с соседними треугольниками, что совсем недопустимо, т.к. вызывает нарушение непрерывности пространства, описываемого треугольниками. Поэтому, в дополнение к основному критерию, необходимо добавить еще один, запрещающий производить смену диагонали в подобных ситуациях. Самыми простыми являются два. Первый показан на рисунке, когда отыскивается точка пересечения прямых, на которых лежат существующая и новая диагональ и проверяется, лежит ли точка пересечения на этих отрезках. Но самым эффективным является второй, когда сравниваются суммы площадей двух треугольников, т.е. площади четырехугольников до и после смены диагоналей. Если суммы совпадают то, новая диагональ не является мнимой. Этот способ особенно эффективен с использованием критерия по площади, т.к. они совместно используют четыре площади треугольников.

Теперь необходимо установить в каком порядке включать эту процедуру. Самым простым решением было проверять циклом каждую грань триангуляции на каждом шаге и, если необходимо, производить смену диагонали. Такой подход и был осуществлен в первой версии рабочего алгоритма, и надежно работал. Но известно, что в треугольной сетке граней больше чем треугольников и узлов в 1,5–1,6, поэтому тотальная проверка всех граней стала бы трудоемкой.

Но по сути тотальной проверки производить не надо т.к. если, например, на предыдущем шаге грань i не нуждалась в смене и, если изменения в сетке, сделанные в этот шаг, не коснулись треугольников, которым принадлежит грань i , то, очевидно, что и на текущем шаге она не нуждается в смене.

Исходя из этого была применена другая технология — технология распространяющегося «вируса смены диагонали». Суть ее заключается в следующем. После выполнения одной из базовых процедур точно известно, какие треугольники сетки подверглись изменениям, т.е. известна область, которая подверглась изменениям. Грани в этой области могут нуждаться в перемене своего направления и эти грани становятся «зараженными». Они помещаются в очередь для проверки — линейный массив индексов. Каждая грань в очереди проверяется и если проверяемая грань нуждалась в изменении, то все остальные грани двух треугольников, содержащих проверяемую грань также становятся зараженными и помещаются в очередь. Другими словами, меняя диагональ, мы изменяем область, состоящую из этих треугольников. Границами этой области будут остальные четыре грани этих двух треугольников. Каждая такая грань как граница измененной области нуждается в проверке. Если же грань не нуждается в изменениях, то она удаляется из очереди. Такой процесс продолжается до тех пор, пока очередь не станет пустой.

Такой подход существенно ускорил работу алгоритма в целом. Например, в одном контрольном примере, для случая с тотальной проверкой время работы на Celeron 266 (333) составило около 18 секунд, а для второго случая время составило менее 10 секунд — сокращение трудоемкости более чем на 45%.
Дополнительные замечания к реализации алгоритма.

Кроме добавления в базовый алгоритм еще одной процедуры, необходимо было усовершенствовать и базовые алгоритмы. Как было сказано выше в базовом алгоритме есть ряд недочетов, которые потребовали своего устроения.

Правильная геометрия фигуры

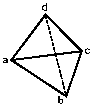
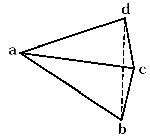
Первый недочет состоял в том, что алгоритм не работал правильно с симметричными или правильными геометрическими формами, которые часто возникают из-за того, что область которую необходимо разбить на элементы является правильной. На рисунке 8 видно, при попытке разбить равнобедренный треугольник bcd с прямым углом по базовой процедуре образуются треугольники нулевой площади (см. рис. 8). В данном случае процедура разобьет треугольник на три: dce, bec, bde . Центр описанной окружности треугольника bcd находится точно на отрезке bd , поэтому треугольник bde имеет нулевую площадь. При попытке вычислить координаты центра его описанной окружности происходит деление на ноль.

Для ликвидации таких случаев. И в первую и во вторую базовую процедуру были введены небольшие относительные поправки к точным координатам середины отрезка и центра описанной окружности, не нарушающие принципы работы алгоритма. Теперь точки стали добавляться не точно в середины сегментов и центры окружностей, а в точки, расположенные вблизи них. Эти поправки добавляет какую-то степень иррациональности в правильную геометрию, и ликвидирует проблему.

Очень вытянутые треугольники с удаленным центром.

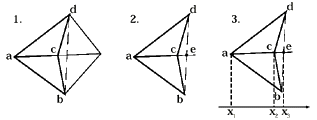
Второй недочет заключается в том, что не учитывается возможность существования таких треугольников, у которых центр описанной вокруг них окружности находится далеко от самого треугольника. В таком случае, при делении треугольников с наименьшим углом в первую очередь, возникает следующая ситуация (см. рис. 9). При первом разделении такого треугольника добавляется точка в центр описанной вокруг него окружности, но так как точка находится далеко от самого треугольника, то сам треугольник не претерпевает никаких изменений и он по-прежнему остается первым в очереди для разбиения.

При следующей попытке разбиения опять вводится новая точка с теми же координатами, что и на предыдущем шаге. В итоге получаются треугольники нулевой площади и грани нулевой длины. Для ликвидации подобных ситуаций была введена проверка на принадлежность вновь вводимой точки к одному из соседних треугольников. Принадлежность к треугольнику устанавливается следующим способом. Для треугольника, зная вершины 1, 2 и 3 треугольника проверяется с какой стороны от грани 1-2 находится проверяемая точка, далее аналогично для граней 2-3 и 3-1. Если для всех граней точка находится с одной стороны, то точка находится внутри треугольника. Математически это определяется довольно просто. Достаточно записать каноническое уравнение прямой на которой лежит грань, подставить в него координаты проверяемой точки и сравнить полученные знаки для каждой грани. Если знаки одинаковые, то и точка находится с одной стороны от всех отрезков.

Малые углы между гранями.

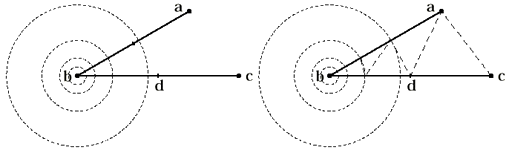
Существует еще одна любопытная подробность, которая даже упомянута у Рапперта. При существовании в исходной геометрии острых углов, т.е. если существует малый угол между соседними сегментами, происходит зацикливание на процедуре деления сегмента (см. рис. 10).

Для ликвидации подобных ситуаций автор алгортима предложил эвристическое правило. Он предложил в таких случаях делить сегмент не посередине, а на ближайшей точке пересечения этого сегмента и концентрических окружностей с центрами в вершине угла (см. рис. 11). Радиус каждой последующей окружности ровно вдвое больше радиуса предыдущей, а первая окружность берется произвольно, но достаточно малой, например r 0 = 0.01 . То есть радиус каждой i -ой окружности равен r i = r 0 2 i .

Безусловно, эту схему надо применять только там, где это действительно необходимо. Поэтому, чтобы ее применить, требуется проверить, надо ли ее проверять. Здесь программисту тоже дается свобода в выборе такой схемы проверки. Можно все же предложить такую схему: сначала проверяется, является ли угол достаточно малым; затем проверяется площадь треугольника, подлежащего разбиению. Если площадь меньше площади, задаваемой как параметр для алгоритма, т.е. критерия максимальной площади, умноженного на какой-то коэффициент, который можно подобрать ( 0 > k ≥ 1 ), то тогда необходимо использовать способ концентрических окружностей.

Если в нашей конструкции к вершине такого угла приложена сосредоточеная сила, то в окрестности этой точки возникают резкие изменения напряжений и деформаций. Задав коэффициент k достаточно малым, мы добьемся более густого разбиения в таких углах.

Все эти усовершенствования коснулись самого алгоритма улучшения сетки. Они объективно позволили улучшить стабильность работы и качество генерируемой сетки, но в нем все же есть небольшие недостатки. Но они не критичны, самым заметным из них является появление неоправданных сгущений сетки. Такие сгущения появляются не всегда, но если и появляются то их можно ликвидировать изменив параметры (минимальный угол или максимальная площадь) и сгенерировав заново сетку. А при разумных установках этих параметров, алгоритм всегда сходится, т.е. достигает этих параметров. Безусловно при более тщательном его исследовании можно добиться еще лучших результатов.
Алгоритм построения первичного разбиения.

Ранее говорилось об алгоритме генерации сетки, но по сути все, о чем говорилось выше, является не алгоритмом генерации сетки, а лишь алгоритмом ее улучшения (Delaunay Refinement Algorithm). Для него входными данными является уже готовое разбиение. Первоначальное разбиение полигональной фигуры производится другим алгоритмом. Входными данными для него являются массивы точек (координаты, нагрузка, закрепление) и граней полигонов, в терминологии Рапперта — сегментов, соединяющих эти точки. Выходные данные — это массив вершин без изменений, массив граней треугольников и массив собственно треугольников, заполняющих весь объем конструкции.

Схематично этот алгоритм можно описать так:

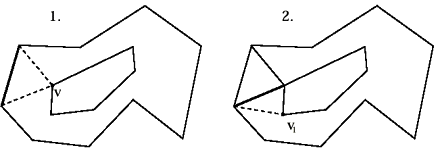
Выбирается начальный сегмент (любой) на внешнем полигоне исходной геометрии. (см. рис. 12)
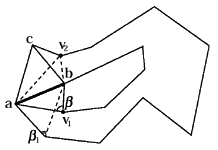
Из всех вершин выбирается такая, из которой лучи, соединяющие эту вершину и концы текущего сегмента образуют максимальный угол.
Добавляется полученный таким образом треугольник и текущим сегментом становится одна из созданных сторон этого трегольника.
Если существует подходящий текущий сегмент, то на шаг 2.

Здесь используется технология, похожая на «вирус смены диагонали». Первым действием является нахождение первого «правильного» треугольника. Таким образом появляются две первых грани (не сегмент, сегментом называется такая грань, которая принадлежит к границам первоначальных полигональных областей — очертаний). Далее треугольники образуются путем правильного добавления к грани еще двух граней соединяющих концы этой грани и определенную точку, принадлежащую сегменту (границе области), добавляя в сетку еще две грани, и т.д.

При выборе третьей вершины для формирования треугольника возникает множество вопросов. Во-первых, необходим критерий, позволяющий легко избежать пересечений вновь создаваемых граней с уже существующими. Во-вторых, как ограничить треугольники от распространения за пределы полигональной области. В-третьих, как правильно сгенерировать первый треугольник. И в-четвертых, как учесть то обстоятельство, что в конструкции присутствуют как отверстия так и заполненные области описываемые одинаково.

Критерием для оптимального выбора третьей точки треугольника является угол, под которым видна грань из этой точки, т.е. угол образуемый двумя лучами, выходящими из выбираемой точки и проходящими через концы грани. Для каждой грани выбирается такая точка, для которой этот угол максимален. Такой выбор критерия позволил сэкономить время на том, что нет необходимости проверять вновь создаваемые грани на пересечение с уже существующими. Для того, чтобы сразу исключить проверки, подобные проверке точки, перед перебором всех точек устанавливается с какой стороны лежит третья точка треугольника, которому принадлежит грань ab (точка c , см. рис. 13). Каждая точка проверяется на то, с какой стороны от грани ab она находится. Другими словами, эта проверка исключает пересечение площадей с уже существующими треугольниками. Я не находил точного обоснования этой особенности, но, тем не менее, такой подход надежно работает.

Чтобы треугольники не распространялись за пределы конструкции, вводится простое правило: треугольники не формируются от сегментов а только от граней уже существующих треугольников. На грани также накладывается ограничение, треугольники формируются только от граней, которые принадлежат только одному треугольнику. Эти правила нарушаются только в одном случае — при генерации первого треугольника.

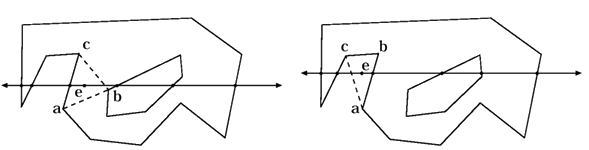
Первый треугольник генерируется от любого сегмента внешнего полигона, а третья точка выбирается также как и для грани. Для первой проверяемой точки устанавливается принадлежность центра треугольника, образуемого этой точкой и сегментом, телу конструкции (см. рис. 14), т.е. лежит ли треугольник внутри контура. Для этого, через этот центр проводится прямая, параллельная оси X и находятся все ее точки пересечения с сегментами.Далее эти точки сортируются по мере возрастания координаты X и формируются интервалы. Каждый нечетный интервал принадлежит контуру.

Все вышеперечисленные процедуры и формируют алгоритм генерации сетки.
Выводы

Описаный алгоритм является завершенным алгоритмом генерации треугольной сетки для плоских полигональных фигур. Этот алгоритм дает теоретически подтвержденные гарантии качества получаемой с его помощью сетки. Прежде всего это касается ограничения сверху «вытянутости» треугольников, т.е. отношения их максимального и минимального габарита в плане.

Приведенный алгоритм адаптирован для построения конечно-элементных сеток, но благодаря своей простоте, может быть легко приспособлен для других задач.