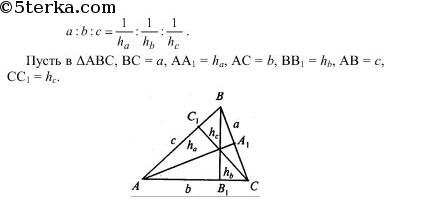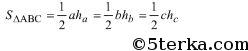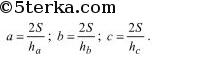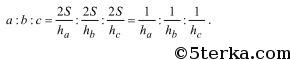Высоты треугольника обратно пропорциональны сторонам

Из полученных равенств получаем

Что и требовалось доказать.

Решебник по геометрии за 9 класс (А.В.Погорелов, 2001 год),
задача №20
к главе «§14. Площади фигур».

Выделите её мышкой и нажмите CTRL + ENTER

Большое спасибо всем, кто помогает делать сайт лучше! =)

Нажмите на значок глаза возле рекламного блока, и блоки станут менее заметны. Работает до перезагрузки страницы.

Высоты треугольника обратно пропорциональны сторонам

@ Наиболее употребимой формулой, связывающей площадь, сторону и высоту на эту сторону, является . Эта формула замечательна тем, что компоненты a и , S и a или S и определяют треугольник неоднозначно, но, тем не менее, можно найти недостающую третью из этих компонент. Необходимо представлять себе расположение высот треугольника в зависимости от его вида: если он остроугольный, то все три высоты внутри него; если он прямоугольный, то одна высота внутри него, а две другие совпадают с катетами; если он тупоугольный, то одна высота внутри него, а две другие, опущенные из острых углов, вне его. Известно, что прямые, содержащие высоты треугольника, пересекаются в одной точке, называемой ортоцентром треугольника (такое название точки связано с тем, что она служит центром вписанной окружности в треугольник, вершины которого являются основаниями высот данного остроугольного треугольника).

а) Доказать, что в любом треугольнике ABC , для любой точки D стороны BC ( D не совпадает с B и C) имеет место равенство ;

б) Доказать, что в любом равностороннем треугольнике ABC сумма расстояний от всякой внутренней точки треугольника до его сторон равна высоте треугольника.

Утверждения а) и б) примера 6.3.1. имеют довольно частое применение при решении заданий вступительных экзаменов, поэтому приведем их краткие доказательства.

а)	Пусть AF – высота треугольника ABC , проведенная из вершины A . Тогда AF является высотой для треугольника ABD и для треугольника ACD . Поэтому и .

Разделив почленно обе части этих равенств, получим требуемое соотношение.

б) Полезно знать, что для построения в тетради равностороннего треугольника используют тот факт, что равнобедренный треугольник с основанием 8 и высотой 7 имеет боковые стороны .

Пусть O – внутренняя точка треугольника ABC и D, E, F – основания перпендикуляров из нее на стороны треугольника. Тогда , т.е. (в ходе преобразований учли, что AB = BC = AC ).

Теперь попытайтесь самостоятельно доказать, что в любом правильном n — угольнике ( n і 3 ) сумма расстояний от любой его внутренней точки до прямых, проходящих через его стороны, есть величина постоянная, равная n Ч r , где r – радиус вписанной в данный n — угольник окружности.

Пример 6.3.2. (КубГУ, эконом., 1987 г.)

В равнобедренном прямоугольном треугольнике длина катета равна 1 . Прямая, проходящая через вершину острого угла, делит площадь треугольника в отношении 1 : 4 . Найти длину отрезка прямой, лежащего внутри треугольника.

Указание : воспользуйтесь рассуждениями в ходе доказательства утверждения примера 6.3.1 а) и учтите две возможности прохождения прямой, делящей площадь треугольника в заданном отношении.

@ Для нахождения площади треугольника часто используют еще две формулы:

; (1) где p – полупериметр треугольника ( формула Герона ) и a, b, c – его стороны.

Пример 6.3.3.

В треугольнике ABC сторона AB = 7 см, AC = 8 см, BC = 9 см. Найти площадь треугольника, образованного высотой и медианой треугольника ABC , проведенных из вершины B .

Эта задача имеет много вариантов решений. Для иллюстрации формул (1) и (2) предлагаем следующий (нелучший) вариант. Решение

Основания высоты и медианы обозначим соответственно через H и M , положим Р A = a . Так как , то по формуле Герона . Точка M делит отрезок AC пополам и поэтому , т.е. .

С другой стороны, , откуда получаем и .
Поэтому , а значит .
Так как , то окончательно (см ).
Ответ: см .
@ Теперь отметим одно очень важное свойство площадей подобных фигур: если фигура подобна фигуре с коэффициентом подобия k, то отношение площадей фигур и равно .

Применим это свойство для решения следующего задания.

Пример 6.3.4. (КубГУ, эконом., 1988 г.)

В треугольнике ABC проведены медианы AM и BK и высота CN . Найти отношение площадей треугольников ABC и MNK . Решение

Изображать медианы AM и BK не будем. В середине стороны AB отметим точку L . Тогда KM, ML, KL – средние линии в треугольнике ABC . Поэтому KM зз AB, KL зз BC и ML зз AC , а значит треугольники MKL и ABC подобны с коэффициентом подобия k = 2 (учли, что ). Поэтому .

Теперь замечаем, что D MKL и D MKN имеют общее основание MK и равные высоты, опущенные на это основание (учли, что MK зз AB ).
Поэтому , и окончательно находим .

Замечание . Из равновеликости треугольников MKL и MKN легко сделать заключение, что площадь любого треугольника, у которого две вершины в точках M и K , а третья на стороне AB , будет равна площади треугольника MKL . Поэтому несущественно, что проведено из вершины C – биссектриса, медиана, выстота или произвольная прямая, пересекающая сторону AB .

@ Отметим, что высоты треугольника обратно пропорциональны сторонам, на которые они опущены, так как , и . Поэтому отрезки, длины которых равны x,y и z, могут служить высотами некоторого треугольника тогда и только тогда, когда сумма меньших чисел из набора , и больше большего числа. Вообще, когда речь идет о высотах треугольника, следует рассматривать его площадь, что в большинстве задач приводит к их решению.

Пример 6.3. 5. (КубГУ, матем., 1994 г.)

Способы нахождения высоты треугольника: теорема и формула

Определение высоты треугольника

Геометрия, являющаяся разделом математики, изучает структуры в пространстве и на плоскости. Одним из типов таких фигур являются геометрические фигуры. К ним можно отнести квадрат, прямоугольник, круг, пятиугольник, треугольник и другие. Из них можно делать более сложные фигуры или оставлять в первоначальном виде.

Треугольником является фигура, относящаяся к классу простых фигур, которая образована тремя точками, находящимися не на одной прямой, и соединенными между собой тремя отрезками.

Треугольники могут быть:

• разными по величине углов: прямоугольными, тупоугольными и остроугольными;
• разными по числу равных сторон: равносторонними, равнобедренными и разносторонними.

Помимо трех сторон, важными элементами треугольников являются медианы, высоты и биссектрисы.

Высотой треугольника является перпендикуляр, опущенный из угла треугольника вниз, на противоположную сторону.

В геометрии высота треугольника обозначается буквой h.

В зависимости от типа треугольника высота может:

• падать на противоположную сторону — у остроугольного треугольника;
• находиться вне треугольника — у тупоугольного треугольника;
• совпадать с одной из сторон — у прямоугольного треугольника.

Чтобы сделать высоту графически явной и понятной на рисунке, ее нередко выделяют красной линией.

Для того чтобы определить графическое начертание высоты треугольника, необходимо:

1. Найти вершину фигуры.
2. Опустить вниз перпендикулярную линию к противоположной стороне.
3. Продлить противоположную сторону до пересечения с высотой, если требуется.

Любой треугольник имеет 3 высоты — по числу углов. Их пересечение находится в точке ортоцентра, которая, в зависимости от типа треугольника, может находиться внутри треугольника, снаружи на пересечении продолжений высот или совпадать с вершиной прямого угла.

Все три высоты треугольника обратно пропорциональны сторонам, к которым опущены. Доказательством будет соотношение:

A × H A ÷ B × H B ÷ C × H C = 1 B C ÷ 1 A C ÷ 1 A B

Выглядеть графически это будет так:

Существует множество способов нахождения высоты треугольника в зависимости от имеющихся данных.

Через площадь и длину стороны, к которой опущена высота:

где S — уже известная площадь треугольника,

Через длины всех сторон:

h = 2 p p × a p × b p × c a

где a, b и c — стороны треугольника,

p — его полупериметр.

Данная формула подходит только для нахождения высоты разностороннего треугольника.

Через длину прилежащей стороны и синус угла:

s i n a — синус угла прилежащей стороны.

Данная формула подходит только для нахождения высоты разностороннего треугольника.

Через стороны и радиус описанной окружности.

Решать задачи с треугольником и описанной окружностью для нахождения высоты можно следующим образом:

где b, c — стороны разностороннего треугольника, к которым не опущена высота,

R — радиус описанной окружности.

Данная формула подходит только для нахождения высоты разностороннего треугольника.

Через длины отрезков, образованных на гипотенузе при проведении к ней высоты треугольника:

где C 1 и С 2 — длины отрезков, образованных на гипотенузе, проведенной к ней высотой.

Данная формула подходит только для нахождения высоты прямоугольного треугольника.

Нахождение высоты равнобедренного треугольника через основание и боковые стороны

Равнобедренным треугольником называют треугольник, имеющий одинаковые по длине катеты, которые образуют равные углы с основанием. В таком треугольнике высота будет опускаться ровно в середину основания, образуя с ним прямой угол.

Помимо высоты, проведенная линия будет являться также осью симметрии, биссектрисой вершинного угла и медианой.

Формула для нахождения высоты в этом случае:

где a — основание,

b — равные боковые стороны.

Свойства высоты в равностороннем треугольнике

Равносторонний треугольник — это треугольник, стороны которого, углы, высоты, медианы, оси симметрии и биссектрисы будут равны.

Такой треугольник является частным примером равнобедренного треугольника, но не наоборот.

Высоту в таком треугольнике можно найти с помощью следующей формулы:

где а — сторона равностороннего треугольника.

Главным свойством, которым обладает высота равностороннего треугольника, является тот факт, что она равна медиане и биссектрисе:

а — сторона правильного равностороннего треугольника.

Нахождение высоты прямоугольного треугольника через его катеты

Прямоугольным считается треугольник, у которого один из углов является прямым, то есть равным 90°. Высота, опущенная из такого угла, падает на гипотенузу треугольника и делит его на два прямоугольных треугольника, которые пропорциональны по отношению к большому треугольнику и друг к другу.

Важно отметить, что две другие высоты будут совпадать с катетами треугольника.

Найти высоту в прямоугольном треугольнике, можно через два его катета (a и b) и гипотенузу (c).

Причем гипотенуза также легко находится через катеты по теореме Пифагора:

Расчет высоты идет следующим образом:

где a, b и c — вышеупомянутые стороны треугольника.

🎦 Видео