Вычислить по формуле грина с окружностью (4 видео)

Интеграл по замкнутому контуру, формула Грина, примеры

Если дан криволинейный интеграл, а кривая, по которой происходит интегрирование — замкнутая (называется контуром), то такой интеграл называется интегралом по замкнутому контуру и обозначается следующим образом:

Область, ограниченную контуром L обозначим D. Если функции P(x, y) , Q(x, y) и их частные производные и — функции, непрерывные в области D, то для вычисления криволинейного интеграла можно воспользоваться формулой Грина:

Таким образом, вычисление криволинейного интеграла по замкнутому контуру сводится к вычислению двойного интеграла по области D.

Формула Грина остаётся справедливой для всякой замкнутой области, которую можно проведением дополнительных линий на конечное число простых замкнутых областей.

Пример 1. Вычислить криволинейный интеграл

если L — контур треугольника OAB , где О(0; 0) , A(1; 2) и B(1; 0) . Направление обхода контура — против часовой стрелки. Задачу решить двумя способами: а) вычислить криволинейные интегралы по каждой стороне треугольника и сложить результаты; б) по формуле Грина.

а) Вычислим криволинейные интегралы по каждой стороне треугольника. Сторона OB находится на оси Ox , поэтому её уравнением будет y = 0 . Поэтому dy = 0 и можем вычислить криволинейный интеграл по стороне OB :

Уравнением стороны BA будет x = 1 . Поэтому dx = 0 . Вычисляем криволинейный интеграл по стороне BA :

Уравнение стороны AO составим, пользуясь формулой уравнения прямой, проходящей через две точки:

Таким образом, dy = 2dx . Вычисляем криволинейный интеграл по стороне AO :

Данный криволинейный интеграл будет равен сумме интегралов по краям треугольника:

б) Применим формулу Грина. Так как , , то . У нас есть всё для того, чтобы вычислить данный интеграл по замкнутому контуру по формуле Грина:

Как видим, получили один и тот же результат, но по формуле Грина вычисление интеграла по замкнутому контуру происходит значительно быстрее.

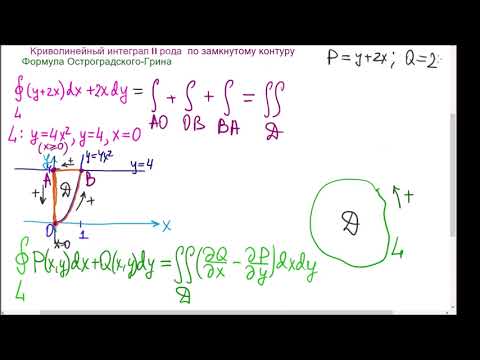
Пример 2. Пользуясь формулой Грина, вычислить криволинейный интеграл

где L — контур OAB , OB — дуга параболы y = x² , от точки О(0; 0) до точки A(1; 1) , AB и BO — отрезки прямых, B(0; 1) .

Решение. Так как функции , , а их частные производные , , D — область, ограниченная контуром L , у нас есть всё, чтобы воспользоваться формулой Грина и вычислить данный интеграл по замкнутому контуру:

Пример 3. Пользуясь формулой Грина, вычислить криволинейный интеграл

, если L — контур, который образуют линия y = 2 − |x| и ось Oy .

Решение. Линия y = 2 − |x| состоит из двух лучей: y = 2 − x , если x ≥ 0 и y = 2 + x , если x .

Имеем функции , и их частные производные и . Подставляем всё в формулу Грина и получаем результат:

Пример 4. С помощью формулы Грина вычислить криволинейный интеграл

если L — окружность .

Решение. Функции , и их частные производные и непрерывны в замкнутом круге . Подставляем всё в формулу Грина и вычисляем данный интеграл:

Содержание

Вычислить по формуле грина с окружностью
Контакты
Формула Грина. Площадь плоской области. Масса кривой
📸 Видео

Видео:Формула Остроградского - ГринаСкачать

Вычислить по формуле грина с окружностью

Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

Видео:Формула ГринаСкачать

Формула Грина. Площадь плоской области. Масса кривой

По этой ссылке вы найдёте полный курс лекций по математике:

Выведем формулу Грина, связывающую криволинейный интеграл по границе L некоторой плоской области D с двойным интегралом по этой области. Теорема 3. Если в замкнутой области D, ограниченной кусочно-гладким контуром L, функции Р(х, у) и Q(x, у) непрерывны и имеют непрерывные частные производные ^ и то справедливо равенство <формула Грина): есь символ § означает интегрирование по границе L области D, причем граница L проходится так, что область D остается слева (рис. 7).

Граница L плоской области D может состоять из одной или нескольких простых замкнутых кривых (компонент). В первом случае она называется односвязной, а во втором — многосвязной. Если граница L состоит из конечного числа кусочно-гладких замкнутых кривых L,-, то кривые Li называются связными компонентами границы. На рис. 8 изображена трехсвязная область.

Односвязная область D (область «без дырок») обладаеттем свойством, чтолюбая лежащая в ней замкнутая кривая может быть стянута в точку Р G D, оставаясь в процессе стягивания в области D. Доказательство теоремы проведем для односвязной области. М В силу свойства линейности достаточно доказать, что Формула Грина Площадь плоской области Масса кривой Площадь цилиндрической поверхности Площадь плоской фигуры Обобщение случай пространственной кривой Докажем первую из этих формул.

Предположим сначала, что кривая L пересекается каждой прямой, параллельной оси Оу, не более чем в двух точках или по целому отрезку (рис. 9). Если каждая такая прямая пересекает кривую L не более чем в двух точках, то кривую L можно разбить на две части L и Ь2 (верхнюю и нижнюю), каждая из которых проектируется взаимно однозначно на некоторый отрезок [а, Ь оси Ох.

Всилуаддитивности криволинейного интеграла имеем На каждой из кривых L и Li возьмем в качестве параметра абсциссу х и запишем уравнения этих кривых сояветстве нно в виде Тогда По предположению производная непрерывна в D, и значит, в силу известной формулы интегрального исчисления, приращение функции можно записать через интеграл от производной этой функции: Из формул получаем Повторный интеграл в правой части последнего соотношения равен двойному инте-фалу от функции ^ по области D, так что окончательно имеем Формула (2) доказана.

Соотношение (3) доказывается аналогично. Складывая почленно соотношения (2) и (3), получаем формулу Грина (1). Отметим, что формула Грина имеет место и для более сложных контуров L, и для неодносвязных областей D. Рассмотрим, например, случай двухсвязной области (рис. 10). Сделаем разрез А В этой области, превращающий ее в односвязную. Тогда Отсюда, учитывая, что получим где интегрирование по кривой L ведется в направлении против движения часовой стрелки, а по кривой Ь2 — в направлении движения часовой стрелки.

Отметим, что при этом кривые L и Ь2 проходятся так, что область D остается слева. Такое направление обхода контура принимается за положительное. Площадь плоской области Возьмем Тогда по формуле Грина (1) получаем где 5 — площадь области D. Отсюда получаем формулу для вычисления площади 5 плоской области D с помощью криволинейного интеграла по границе L этой области: (7) Прммр. Вычислить площадь области, ограниченной эллипсом L: Запишем уравнение эллипса в параметрической форме .

Искомая площадь находится по формуле (7), где криволинейный интеграл берется по эллипсу при обходе контура в положительном направлении, что соответствует изменен ик> параметра t от 0 до 2я. Так как то отсюда получаем, что Замечание. Пусть в пространстве задана ориентированная кусочно-гладкая кривая AD и пусть, кроме того, в некоторой области П, содержащей кривую AD, задана вектор-функция — непрерывные в О функции.

Аналогично плоскому случаю криволинейный интеграл от вектор-функции F по ориентированной кривой АВ определим выражением Масса кривой В примере 1 из § 1 было показано, что масса кривой L вычисляется с помощью интеграла 1-го рода где /(М) — переменная линейная плотность на кривой L. (Мы предполагаем, что f(M) — непрерывная фунмция на АВ.) 4.2. Площадь цилиндрической поверхности Пусть в плоскости хОу задана некоторая спрямляемая (т. е. имеющая длину) кривая АВ и на этой кривой определена непрерывная функция f(M) ^ 0.

Тогда совокупность точек (х, у, f(x, у)), или (М, /(М)), составит некоторую кривую, лежащую на цилиндрической поверхности, для которой кривая АВ является направляющей, а ее образующая параллельна оси Oz.

Требуется определить площадь цилиндрической поверхности ABDC, о»раниченной снизу кривой АВУ сверху — кривой z — f(M), где М € АВ, и вертикальными прямыми АС и BD (рис. 11). Для решения этой задачи поступим так: 1) разобьем кривую АВ на п частей точками так, как показано на рис. 11; 2) из каждой точки Мк проведем перпендикуляр к плоскости хОу высотой f(Mk) (при этом цилиндрическая поверхность А В DC разобьется на п полосок);

3) кажаую полоску заменим прямоугольником с основанием — длина дуги МкМк+, и высотой, равной значению функции /(М) в какой-нибудь точке этой дуги, например, в точке Мк. Тогда площадь fc-ой полоски будет приближенно равна. а площадь всей поверхности ABDC Это приближенное равенство будет тем точнее, чем мельче будут частичные дуги , на которые разбита кривая АВ. Пусть Д/ — наибольшая из длин А1к частичных .цт .

Возможно вам будут полезны данные страницы:

Тогда при 0 в пределе получим точное значение искомой площади Предел справа по определению есть криволинейный интеграл первого рода от функции /(Af) по кривой АВ. Итак, (2) Пример 1. Вычислить площадь части боковой поверхности цилиндра срезанного сверху поверхностью Сведем задачу к вычислению криволинейного интеграла t-ro рода от функции вдоль дуги окружности, расположенной в первой четверти. Будем иметь Параметрические уравнения линии Формула Грина Площадь плоской области Масса кривой.

Площадь цилиндрической поверхности Площадь плоской фигуры Обобщение случай пространственной кривой Площадь плоской фигуры Ранее мы установили, что площадь 5 плоской фигуры D, ограниченной линией L, вычисляется по формуле Правая часть есть криволинейный интеграл 2-го рода. 4.4. Работа силы Пусть в некоторой плоской области D, содержащей кривую АВУ задана сила где функции , а следовательно, и F(М) предполагаются непрерывными функциями точки ЛГ.

Требуется найти работу силы F, если под действием этой силы материальная точка М, имеющая единичную массу, переместилась из точки А в точку В по кривой АВ. Для решения этой задачи разделим кривую АВ на п частей точками (рис. 12), заменим каждую дугу хордой , предполагая для простоты , что на участке кривой (а значит, и на хорде сила Ffc имеет постоянное значение, например, равное ее значению в точке получим приближенное выражение работы силы на участке пути где — длина вектора — длина вектора.

Из формулы (4) с учетом (5) получим или Так как правая частьформулы (6) есть скалярное произведение векторов то, учитывая (7) и (8), будем иметь Суммируя по всем значениям , получим величину принимают за точное значение работы. Но с другой стороны, предел этой суммы есть криволинейный интеграл 2-го рода от вектор-функции F(M) по кривой АВ.

Итак, работа силы вычисляется по формуле Рис. 12 ( Пример 2. Найти работу силы при перемещении единичной массы по параболе 4 Применим формулу (9), положив в ней Так как то искомую работу можо вычислить так: Обобщение на случай пространственной кривой (рис. 14). Если в некоторой пространственной области П, содержащей пространственную кривую АВ, задана сила — непрерывные функции в области П, то рабога, совершаемая силой F(M) по перемещению материальной точки М с единичной массой из точки А в точку В по пространственной кривой АВ, равна Упражнения.

Вычислите криволинейные интегралы 1-го рода: 1. — четверть элл ипса ^ + = 1, л ежащая в первом квадранте. — окружность — отрезок прямой, соединяющий точки отреэо к прямой, соединяющий точки (— дуга параболы у2 = 2х от точки (0,0) до точки (I, первый виток винтовой линии Найдите длину дуги конической винтовой линии х — ас* cost, у = от точки .до точки 2?(а,0,а). Указание: точке А соответствует- значение параметра t( = -оо, а точке В — значение t2 = 0. 8. Найдите площадь боковой поверхности кругового цилиндра, находящейся под первым витком винтовой линии и выше плоскости z = 0. 9.

Вычислить по формуле грина с окружностью

Найдите координаты центра тяисести

однородной полуарки циклоиды Вычислите криволинейные интегралы 2-го рода: дуга кривой у = х3 отточки (0,0) до точки верхняя половина эллипса , пробегаемая против хода часовой стрелки. где точки соединены кривой Ч2Г при . — дуга первой арки циклоиды пробегаемая в направлении возрастания параметра t. — окружность , пробегаемая против хода часовой стрелки. Указание . Используйте параметрические уравнения окружности. — виток винтовой линии — ломаная с вершинами 17.

Найдите массу дуги AB кривой у = lnz, если в каждой ее точке линейная плотность пропорциональна квадрату абсциссы точки, причем . 18. Найдите длину дуги кривой j между ее точками пересечения с осями координат. 19. Найдите площадь, ограниченную астроидой 20. Найдите работу силового поля j, когда точка массы m описывает окружность х = а соs t, у = a sin t, двигаясь по ходу часовой стрелки. 21. Поле образовано силой .

Вычислите работу при перемещении единицы массы по контуру квадрата со сторонами Применив формулу Пэина, вычислите интегралы в задачах 22-24: по контуру ЬАВС с вершинами по контуру фигуры, ограниченной линиями у вдоль единичной окружности в положительном направлении Формула Грина Площадь плоской области Масса кривой Площадь цилиндрической поверхности.

Площадь плоской фигуры Обобщение случай пространственной кривой — вдоль контура квадрата с вершинами в точках Л(1,0), при положительном направлении обхода. Ответы Указание. Перейдите к полярным координатам. Указание. Воспользуйтесь формулами (в зависимости от направления обхода).. Указание. Данный интеграл несобстве нный, так как в точках пересечения контура интегрирования с прямой х + у = 0 подынтегральн ос выражение принимает вид g. Формулу фина применять нельзя.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.