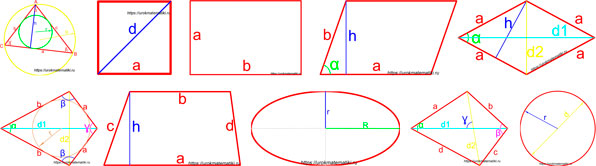
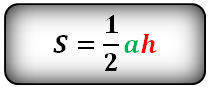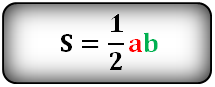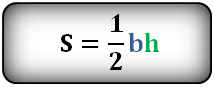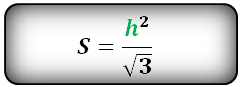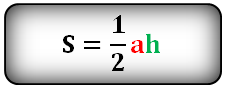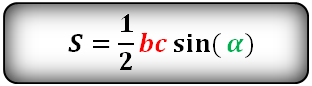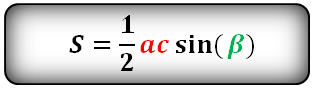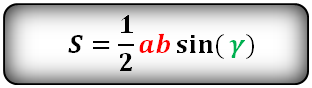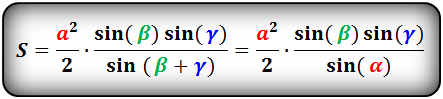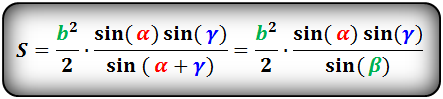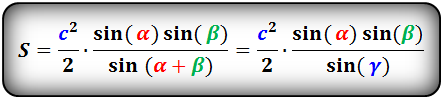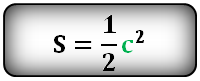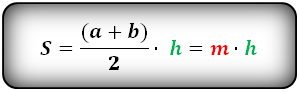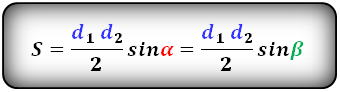Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
- Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
- Формула площади треугольника по трем сторонам
- Формула площади треугольника по двум сторонам и углу между ними
- Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
- Формулы площади квадрата
- Формула площади квадрата по длине стороны
- Формула площади квадрата по длине диагонали
- Формула площади прямоугольника
- Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
- Формула площади параллелограмма по двум сторонам и углу между ними
- Формула площади параллелограмма по двум диагоналям и углу между ними
- Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
- Формула площади ромба по длине стороны и углу
- Формула площади ромба по длинам его диагоналей
- Формулы площади трапеции
- Формула Герона для трапеции
- Формула площади трапеции по длине основ и высоте
- Формулы площади дельтоида
- Формула площади дельтоида по двум неравным сторонам и углу между ними
- Формула площади дельтоида по равным сторонам и углу между ними
- Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности
- Формула площади дельтоида по двум диагоналям
- Формулы площади произвольного выпуклого четырехугольника
- Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними
- Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов
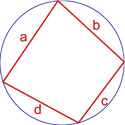
- Формула площади вписанного четырехугольника (формула Брахмагупты)
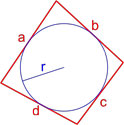
- Формула площади четырехугольника с вписанной окружностью
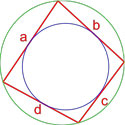
- Формула площади четырехугольника с вписанной и описанной окружностями
- Формулы площади круга
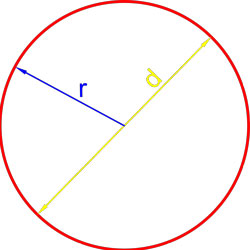
- Формула площади круга через радиус
- Формула площади круга через диаметр
- Площадь сегмента круга
- Площадь кругового сегмента через угол в градусах.
- Площадь кругового сегмента через угол в радианах.
- Формула площади эллипса
- Как найти площадь параллелограмма, треугольника, трапеции
- Площадь параллелограмма
- Площадь треугольника
- Готовые работы на аналогичную тему
- Площадь трапеции
- Пример задачи
- Формулы площадей всех основных фигур
- 1. Формула площади круга через радиус или диаметр
- 2. Формула расчета площади треугольника
- 3. Площадь треугольника, формула Герона
- 4. Площадь прямоугольного треугольника по катетам
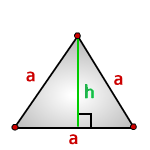
- 5. Как вычислить площадь равнобедренного треугольника ?
- 6. Площадь равностороннего треугольника равна:
- 7. Найти площадь треугольника, угол и две стороны
- 8. Площадь треугольника по стороне и двум углам, формула.
- 9. Формула расчета площади прямоугольника
- 10. Как рассчитать площадь квадрата через диагональ или сторону
- 11. Формулы площади параллелограмма
- 12. Площадь произвольной трапеции
- 13. Площадь равнобедренной трапеции
Видео:Площадь параллелограмма треугольника и трапецииСкачать

Формулы площади треугольника
Формула площади треугольника по стороне и высоте
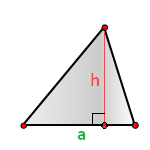
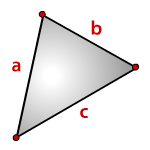
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
где a — одна из сторон треугольника, h — высота, проведенная к стороне треугольника.
Формула площади треугольника по трем сторонам
Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c .
S = p p — a p — b p — c ,
где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.
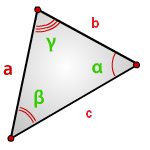
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = 1 2 a · b · sin γ ,
где a, b — стороны треугольника,
γ — угол между сторонами a и b .
Формула площади треугольника по трем сторонам и радиусу описанной окружности
a, b, c — стороны треугольника,
R — радиус описанной окружности.
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
где S — площадь треугольника,
r — радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c 2
Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Формулы площади квадрата
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
где S — площадь квадрата,
a — длина стороны квадрата.
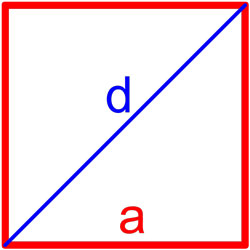
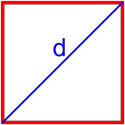
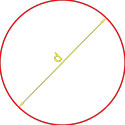
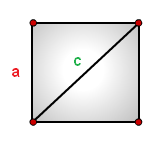
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.
где S — площадь квадрата,
d — длина диагонали квадрата.
Видео:8 класс, 13 урок, Площадь параллелограммаСкачать

Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторон.
где S — площадь прямоугольника,
a, b — длины сторон прямоугольника.
Видео:Геометрия 8 класс (Урок№9 - Площадь параллелограмма.)Скачать

Формулы площади параллелограмма
Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны.
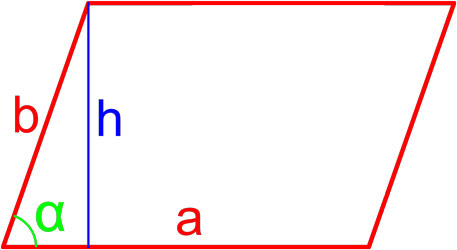
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
где S — площадь параллелограмма,
a, h — длины сторон параллелограмма.
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
где S — площадь параллелограмма,
a, b — длины сторон параллелограмма,
α — угол между сторонами параллелограмма.
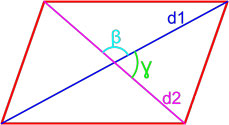
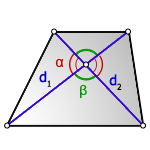
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.
S = d1 · d2 · sin β 2 = d1 · d2 · sin γ 2 ,
где S — площадь параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
β , γ — угол между диагоналями параллелограмма.
Видео:КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

Формулы площади ромба
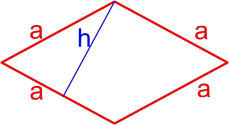
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
где S — площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба.
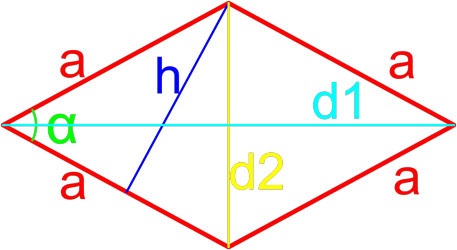
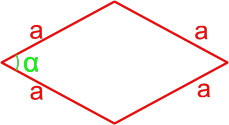
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
где S — площадь ромба,
a — длина стороны ромба,
α — угол между сторонами ромба.
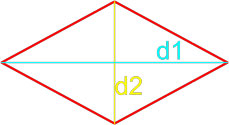
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.
где S — площадь ромба,
d1, d2 — длины диагоналей ромба.
Видео:Площадь параллелограмма, треугольника, трапецииСкачать

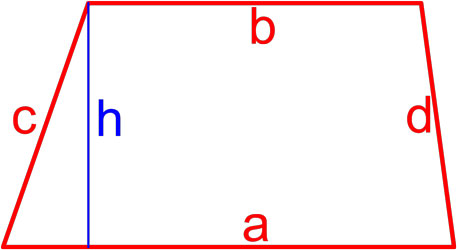
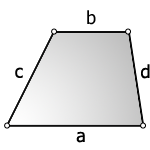
Формулы площади трапеции
Трапеция — это четырёхугольник, у которого две ( a, b ) стороны параллельны (основания), а две другие ( c, d ) стороны не параллельны (боковые стороны).
Формула Герона для трапеции
где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,
p = a + b + c + d 2 — полупериметр трапеции.
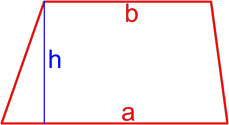
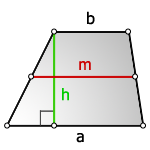
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы её оснований на высоту.
где S — площадь трапеции,
a, b — длины основ трапеции,
h — высота трапеции.
Видео:Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Формулы площади дельтоида
Дельтоид — это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания.
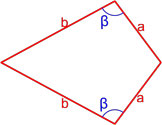
Формула площади дельтоида по двум неравным сторонам и углу между ними
Площадь дельтоида равна произведению длин неравных сторон на синус угла между ними.
где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
β — угол между неравными сторонами дельтоида.
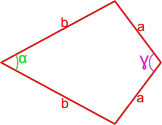
Формула площади дельтоида по равным сторонам и углу между ними
Площадь дельтоида равна полусумме произведения каждой из пар равных сторон на синус угла между ними.
S = a 2 sin γ + b 2 sin α 2 ,
где S — площадь дельтоида,
a, b — длины сторон дельтоида,
α — угол между равными сторонами b ,
γ — угол между равными сторонами a .
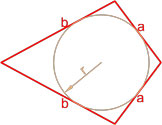
Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности
Площадь дельтоида равна произведению суммы неравных сторон на радиус вписанной окружности.
где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
r — радиус вписанной окружности.
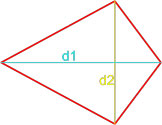
Формула площади дельтоида по двум диагоналям
Площадь дельтоида равна половине произведения длин двух диагоналей.
где S — площадь дельтоида,
d1, d2 — диагонали дельтоида.
Видео:Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Формулы площади произвольного выпуклого четырехугольника
Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними
Площадь произвольного выпуклого выпуклого четырехугольника равна половине произведения его диагоналей умноженной на синус угла между ними.
S = d1 · d2 · sin γ 2 ,
где S — площадь четырехугольника,
d1, d2 — диагонали четырехугольника,
γ — любой из четырёх углов между диагоналями.
Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника,
θ = α + β 2 — полусумма двух противоположных углов четырехугольника.
Формула площади вписанного четырехугольника (формула Брахмагупты)
Если вокруг четырехугольника можно описать окружность, то его площадь равна
S = p — a p — b p — c p — d ,
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника.
Формула площади четырехугольника с вписанной окружностью
Если в четырехугольник можно вписать окружность, то его площадь равна:
где S — площадь четырехугольника,
r — радиус вписанной окружности,
p = a + b + c + d 2 — полупериметр четырехугольника.
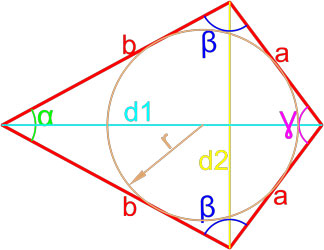
Формула площади четырехугольника с вписанной и описанной окружностями
Если в четырехугольник можно вписать окружность, а также около него можно описать окружность, то его площадь равна:
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника.
Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

Формулы площади круга
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.
где S — площадь круга,
r — радиус круга.
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.
где S — площадь круга,
d — диаметр круга.
Видео:Геометрия 8 класс. Площадь параллелограммаСкачать

Площадь сегмента круга
Площадь кругового сегмента через угол в градусах.
где S — площадь сегмента круга,
R — радиус круга,
α° — угол в градусах.
Площадь кругового сегмента через угол в радианах.
где S — площадь сегмента круга,
R — радиус круга,
α° — угол в радианах.
Видео:Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать

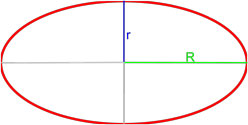
Формула площади эллипса
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
где S — площадь эллипса,
a — длина большей полуоси эллипса,
b — длина меньшей полуоси эллипса.
Видео:Геометрия 9 класс (Урок№14 - Теорема о площади треугольника.)Скачать

Как найти площадь параллелограмма, треугольника, трапеции
Вы будете перенаправлены на Автор24
Видео:8 класс, 14 урок, Площадь треугольникаСкачать

Площадь параллелограмма
Площадь параллелограмма определяется как произведение длины его стороны, на высоту, проведенную к ней.
Математически это можно записать следующим образом
где $a$ сторона параллелограмма, $h$ — высота, проведенная к этой стороне.
Доказательство.
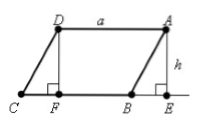
Пусть нам дан параллелограмм $ABCD$, у которого $AD=BC=a$. Проведем высоты $DF$ и $AE$ (рис. 1).
Очевидно, что фигура $FDAE$ — прямоугольник.
[angle BAE=^0-angle A, ] [angle CDF=angle D-^0=^0-angle A-^0=^0-angle A=angle BAE]
Следовательно, так как $CD=AB, DF=AE=h$, по $I$ признаку равенства треугольников $triangle BAE=triangle CDF$. Тогда
Значит по теореме о площади прямоугольника:
Теорема доказана.
Площадь параллелограмма определяется как произведение длины его смежных сторон, на синус угла между этими сторонами.
Математически это можно записать следующим образом
где $a, b$ стороны параллелограмма, $alpha $ — угол между ними.
Доказательство.
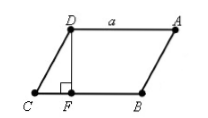
Пусть нам дан параллелограмм $ABCD$, у которого $BC=a, CD=b, angle C=alpha $. Проведем высоту $DF=h$ (рис. 2).
По определению синуса, получим
Значит, по теореме $1$:
Теорема доказана.
Видео:8 класс. Площадь параллелограмма. Геометрия.Скачать

Площадь треугольника
Площадь треугольника определяется как половина произведения длины его стороны, на высоту, проведенную к ней.
Математически это можно записать следующим образом
где $a$ сторона треугольника, $h$ — высота, проведенная к этой стороне.
Доказательство.
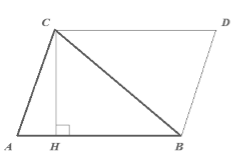
Пусть нам дан треугольник $ABC$, у которого $AB=a$. Проведем высоту $CH=h$. Достроим его до параллелограмма $ABCD$ (рис. 3).
Очевидно, что по $I$ признаку равенства треугольников $triangle ACB=triangle CDB$. Тогда
Значит по теореме $1$:
Теорема доказана.
Готовые работы на аналогичную тему
Площадь треугольника определяется как половина произведения длины его смежных сторон, на синус угла между этими сторонами.
Математически это можно записать следующим образом
где $a, b$ стороны треугольника, $alpha $ — угол между ними.
Доказательство.
Пусть нам дан треугольник $ABC$, у которого $AB=a$. Проведем высоту $CH=h$. Достроим его до параллелограмма $ABCD$ (рис. 3).
Очевидно, что по $I$ признаку равенства треугольников $triangle ACB=triangle CDB$. Тогда
Значит по теореме $1$:
Теорема доказана.
Видео:площадь ТРЕУГОЛЬНИКА площадь ПАРАЛЛЕЛОГРАММА площадь ТРАПЕЦИИ 8 классСкачать

Площадь трапеции
Площадь трапеции определяется как половина произведения суммы длин его оснований, на его высоту.
Математически это можно записать следующим образом
Доказательство.
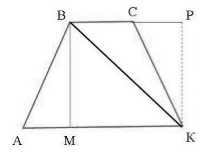
Пусть нам дана трапеция $ABCK$, где $AK=a, BC=b$. Проведем в ней высоты $BM=h$ и $KP=h$, а также диагональ $BK$ (рис. 4).
По теореме $3$, получим
Теорема доказана.
Видео:Площадь параллелограмма по векторамСкачать

Пример задачи
Найти площадь равностороннего треугольника, если длина его стороны равняется $a.$
Решение.
Так как треугольник равносторонний, то все его углы равняются $^0$.
Тогда, по теореме $4$, имеем
Заметим, что результат этой задачи можно применять при нахождении площади любого равностороннего треугольника с данной стороной.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 19 05 2021
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Формулы площадей всех основных фигур
Видео:Площади фигур. Повторяем формулы и решаем задачи. Вебинар | МатематикаСкачать

1. Формула площади круга через радиус или диаметр
Зная диаметр или радиус круга, можно найти его площадь.
r — радиус круга
D — диаметр
Формула площади круга, (S):
Видео:Все формулы площади параллелограмма 🔥 #умскул_профильнаяматематика #никитасалливан #егэпрофильСкачать

2. Формула расчета площади треугольника
h — высота треугольника
a — основание
Площадь треугольника (S):
3. Площадь треугольника, формула Герона
a , b , c , — стороны треугольника
p— полупериметр, p=( a + b + c )/2
Формула ( Герона ) площади треугольника через полупериметр ( S ):
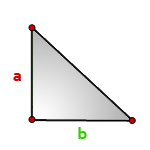
4. Площадь прямоугольного треугольника по катетам
Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.
a , b — катеты треугольника
Формула площади прямоугольного треугольника, (S):
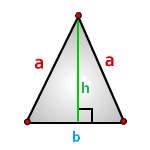
5. Как вычислить площадь равнобедренного треугольника ?
b — основание треугольника
a — равные стороны
h — высота
Формула площади треугольника через высоту h и основание b , ( S ):
Формула площади треугольника через, стороны a , b , (S):

6. Площадь равностороннего треугольника равна:
Формулы расчета, площади равностороннего треугольника.
a — сторона треугольника
h — высота
Площадь треугольника только через сторону a , (S):
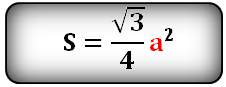
Площадь треугольника только через высоту h , ( S ):
Площадь треугольника через сторону a и высоту h , (S):
7. Найти площадь треугольника, угол и две стороны
Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.
a , b , c — стороны треугольника
α , β , γ — углы
Формулы площади треугольника, через две стороны и угол между ними, ( S ):
8. Площадь треугольника по стороне и двум углам, формула.
a , b , c — стороны треугольника
α , β , γ — противолежащие углы
Площадь треугольника через сторону и два угла (S):
9. Формула расчета площади прямоугольника
b — длина прямоугольника
a — ширина
Формула площади прямоугольника, (S):
10. Как рассчитать площадь квадрата через диагональ или сторону
a — сторона квадрата
c — диагональ
Формула площади квадрата через сторону a , (S):
Формула площади квадрата через диагональ c , (S):
11. Формулы площади параллелограмма
1. Формула площади параллелограмма через стороны и углы
a, b — стороны параллелограмма
α , β — углы параллелограмма
Формула площади через стороны и углы параллелограмма, ( S ):
2. Формула площади параллелограмма через сторону и высоту
a, b — стороны параллелограмма
H b — высота на сторону b
H a — высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):
3. Формула площади параллелограмма через диагонали и угол между ними
D — большая диагональ
d — меньшая диагональ
α , β — углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):
12. Площадь произвольной трапеции
1. Формула площади трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
m — средняя линия
h — высота трапеции
Формула площади трапеции, (S):
2. Формула площади трапеции через диагонали и угол между ними
d 1, d 2 — диагонали трапеции
α , β — углы между диагоналями
Формула площади трапеции, (S):
3. Формула площади трапеции через четыре стороны
b — верхнее основание
a — нижнее основание
c, d — боковые стороны
Формула площади трапеции, (S):
13. Площадь равнобедренной трапеции
1. Формула площади равнобедренной трапеции через стороны и угол
b — верхнее основание
a — нижнее основание
c — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобокой трапеции через радиус вписанной окружности
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α , β — углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α , β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
m — средняя линия трапеции
c — боковая сторона
α , β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):