Какое из следующих утверждений верно?
1) Отношение площадей подобных треугольников равно коэффициенту подобия.
2) Диагонали прямоугольника точкой пересечения делятся пополам.
3) Биссектриса треугольника делит пополам сторону, к которой она проведена.
В ответе запишите номер выбранного утверждения.
1) Отношение площадей подобных треугольников равно коэффициенту подобия. — неверно, отношение площадей равно квадрату коэффициента подобия.
2) Диагонали прямоугольника точкой пересечения делятся пополам. — верно, из свойства диагоналей прямоугольника.
3)Биссектриса треугольника делит пополам сторону, к которой она проведена. — неверно, биссектриса делит угол, из которого выходит, на два равных угла.
Видео:Площади треугольников с равным углом.Скачать

Основные свойства площадей треугольников
Факт 1.
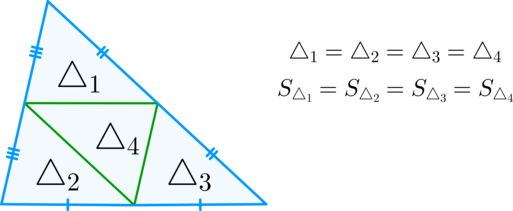
(bullet) Средние линии треугольника разбивают его на 4 равных треугольника.
Соответственно, площади этих треугольников равны.
Факт 2.
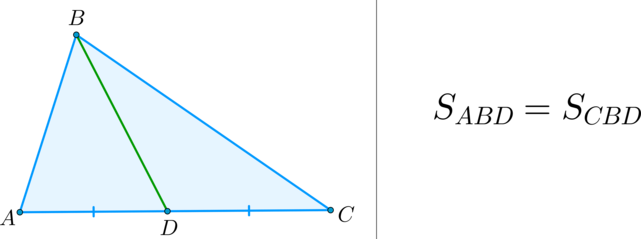
(bullet) Медиана треугольника делит его на два треугольника, равных по площади (равновеликих).
Факт 3.
(bullet) Все 3 медианы треугольника делят его на 6 равновеликих треугольников.
Факт 4.
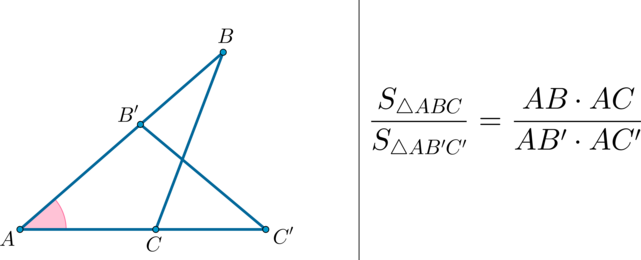
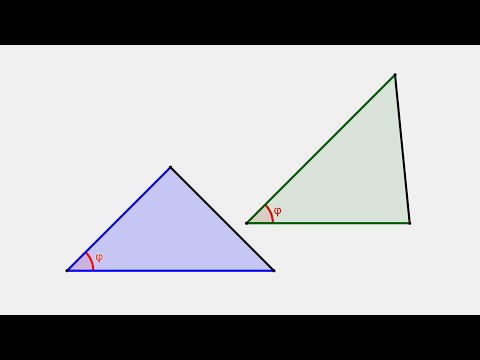
(bullet) Площади треугольников, имеющих одинаковый угол, относятся как произведения сторон, образующих этот угол.
Факт 5.
(bullet) Площади треугольников, имеющих одинаковое основание, относятся как высоты, проведенные к этим основаниям.
Факт 6.
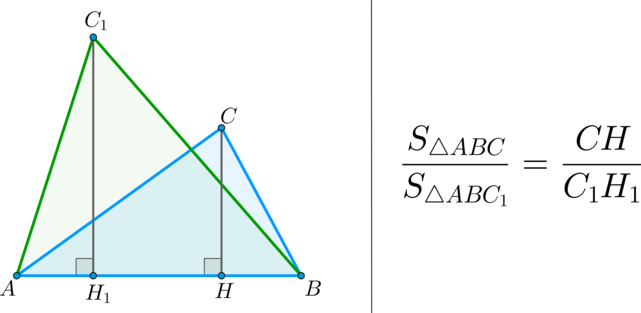
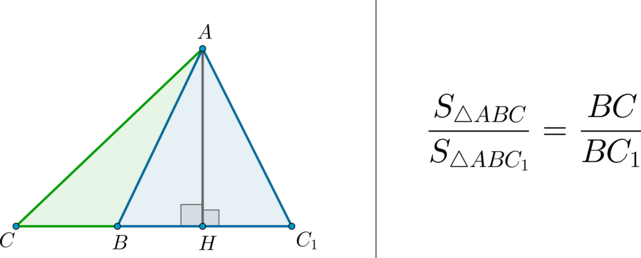
(bullet) Площади треугольников, имеющих одинаковую высоту, относятся как основания, к которым проведена эта высота.
Факт 7.
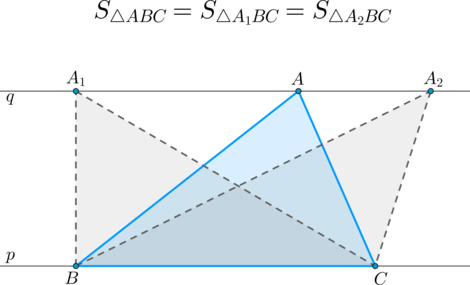
(bullet) Если прямые (p) и (q) параллельны, то
Факт 8.
(bullet) Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
(bullet) Отношение периметров подобных треугольников равно коэффициенту подобия.
Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Основные сведения об отношении площадей подобных треугольников
Видео:Отношение площадей треугольников с равным угломСкачать
Понятие подобия треугольников
Два треугольника называются подобными, если их углы попарно равны, а стороны, лежащие напротив соответственных углов пропорциональны.
A B / K L = B C / L M = A C / K M = k , ∠ A = ∠ K , ∠ B = ∠ L , ∠ C = ∠ M ⇒ Δ A B C
Отношение длин подобных треугольников называют коэффициентом подобия (k).
Также пропорциональные стороны подобных треугольников могут быть названы сходственными сторонами.
В подобных треугольниках, кроме сторон, подобны и другие величины: биссектрисы, медианы, высоты и т.д.
Видео:Геометрия 8 класс : Отношение площадей подобных треугольниковСкачать

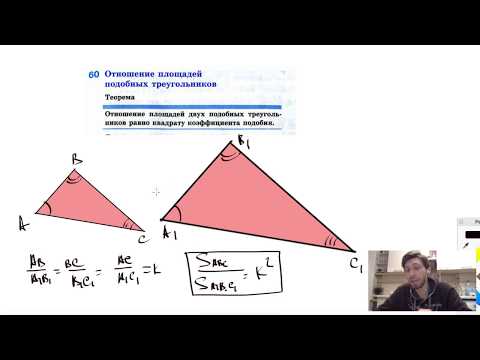
Теорема об отношении площадей подобных треугольников
Формулировка теоремы: отношение площадей подобных треугольников равно квадрату коэффициента подобия.
В геометрии существует три признака подобия треугольников:
1. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
3. Если три стороны одного треугольника пропорциональны двум сторонам другого треугольника, то такие треугольники подобны.
Свойства подобных треугольников:
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
- Отношение периметров подобных треугольников равно коэффициенту подобия.
- Отношение длин соответствующих элементов подобных элементов равно коэффициенту подобия.
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Доказательство теоремы
Докажем теорему об отношении площадей подобных треугольников.
Теорема: отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство: изобразим подобные треугольники Δ A B C
Из подобия треугольников по определению следует: A B / K L = B C / L M = A C / K M = k .
Воспользуемся следующей теоремой: если у двух треугольников равны углы (∠A=∠K), то их площади относятся, как произведение сторон, заключающих данные углы. Запишем в виде формулы:
Что и требовалось доказать.
Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Примеры решения задач
Площади подобных треугольников ΔABC и ΔA1B1C1 равны соответственно 200 см² и 50 см². Сторона A1B1=5 см. Найдите сходственную ей сторону AB треугольника ABC.
По теореме об отношении площадей подобных треугольников: S a b c / S a 1 b 1 c 1 = k ² ⇒ 200 / 50 = k ² ⇒ k = 2 .
A B / A 1 B 1 = 2 , A B = A 1 B 1 * 2 , A B = 5 * 2 = 10 с м .
ΔABC и ΔA1B1C1 — подобны. Сходственные стороны AC и A1C1 соответственно равны 13 см и 0,1 м.
Найдите отношение периметров ΔABC и ΔA1B1C1.
A 1 C 1 = 0 , 1 м = 10 с м
A C / A 1 C 1 = 13 / 10 = 1 , 3 ⇒ P a b c / P a 1 b 1 c 1 = 1 , 3
Видео:Задача по геометрии № 25 ОГЭ на отношение площадейСкачать

Задача для самостоятельной работы
Треугольники Δ A B C
Δ K L M подобны. Площадь ΔABC равна 500 см², площадь ΔKLM равна 125 см². Сторона AC равна 18 см, найти сходственную ей сторону KM.
Проверьте, насколько верный или неверный ваш ответ.
Советуем составить краткий конспект для подготовки к уроку.
💡 Видео
Отношение площадей треугольниковСкачать
#Отношение площадей треугольников имеющих обую высотуСкачать

Геометрия 8 класс (Урок№14 - Определение подобных треугольников. Отношение площадей подобных фигур.)Скачать

Подобные треугольникиСкачать

Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

60. Отношение площадей подобных треугольниковСкачать
Геометрия Раскрыта тайна площадей треугольниковСкачать

Отношение площадей подобных треугольниковСкачать

9 класс, 12 урок, Теорема о площади треугольникаСкачать

Задание 26 Отношения площадей треугольниковСкачать

ЕГЭ Задание 16 Отношение площадей подобных треугольниковСкачать

Какая из площадей больше? Треугольники с общей высотой. геометрия 8 классСкачать

Отношение площадей подобных треугольников.Скачать