Окружность

Окружностью называется фигура, состоящая из всех точек плоскости, находящихся от данной точки на данном расстоянии. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности.

Часть плоскости, ограниченная окружностью называется кругом.

Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Сегментом называется часть круга, ограниченная дугой и стягивающей ее хордой.

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Основные термины

Касательная

Прямая, имеющая с только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Свойства касательной

1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Хорда

Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром.

Свойства хорд

1. Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.

Дуги, заключенные между параллельными хордами, равны.

Если две хорды окружности, AB и CD пересекаются в точке M , то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD.

Видео:Интересное свойство касающихся окружностей с общей касательнойСкачать

Свойства окружности

1. Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку ( касательная ); иметь с ней две общие точки ( секущая ).
2. Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
3. Точка касания двух окружностей лежит на линии, соединяющей их центры.

Теорема о касательной и секущей

Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC 2 = MA•MB .

Теорема о секущих

Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть. MA•MB = MC•MD.

Видео:Пара касающихся окружностей | Осторожно, спойлер! | Борис Трушин |Скачать

Углы в окружности

Центральным углом в окружности называется плоский угол с вершиной в ее центре.

Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом.

Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. Мерой дуги может служить мера соответствующего ей центрального угла.

Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.

Свойства углов, связанных с окружностью

1. Вписанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°.

Углы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на диаметр, равен 90°.

Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.

Видео:Касающиеся окружности.Скачать

Длины и площади

1. Длина окружности C радиуса R вычисляется по формуле:

Площадь S круга радиуса R вычисляется по формуле:

Длина дуги окружности L радиуса R с центральным углом ,измеренным в радианах, вычисляется по формуле:

Площадь S сектора радиуса R с центральным углом в радиан вычисляется по формуле:

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Вписанные и описанные окружности

Окружность и треугольник

• центр вписанной окружности — точка пересечения биссектристреугольника, ее радиус r вычисляется по формуле:

где S — площадь треугольника, а — полупериметр;

центр описанной окружности — точка пересечения серединных перпендикуляров, ее радиус R вычисляется по формуле:

здесь a, b, c — стороны треугольника, — угол, лежащий против стороны a , S — площадь треугольника;

Окружность и четырехугольники

• около выпуклого четырехугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180°:

в четырехугольник можно вписать окружность тогда и только тогда, когда у него равны суммы противоположных сторон:

• около параллелограмма можно описать окружность тогда и только тогда, когда он является прямоугольником;
• около трапеции можно описать окружность тогда и только тогда, когда эта трапеция — равнобедренная; центр окружности лежит на пересечении оси симметрии трапеции с серединным перпендикуляром к боковой стороне;
• в параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом.

Видео:Касание окружностейСкачать

Основные теоремы, связанные с окружностями

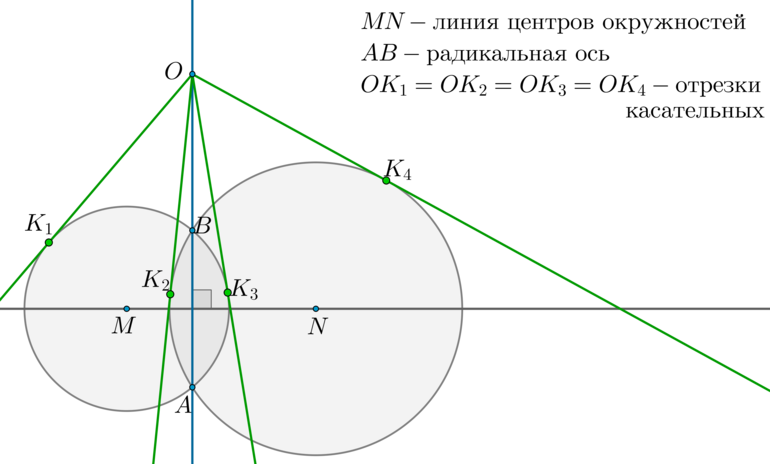
Радикальная ось — прямая, проходящая через точки пересечения двух окружностей.
Линия центров окружностей — прямая, проходящая через центры двух окружностей.

Теорема 1.

1) Радикальная ось перпендикулярна линии центров окружностей.
2) Отрезки касательных, проведенных из любой точки радикальной оси к этим окружностям, равны.

Доказательство:

1) Рассмотрим (triangle BMN) и (triangle AMN) : они равны по трем сторонам ( (BM=AM=R_1, BN=AN=R_2) — радиусы первой и второй окружностей соответственно). Таким образом, (angle BNM=angle ANM) , следовательно, (MN) — биссектриса в равнобедренном (triangle ANB) , следовательно, (MNperp AB) .

2) Отметим произвольную точку (O) на радикальной оси и проведем касательные (OK_1, OK_3) к первой окружности и (OK_2, OK_4) ко второй окружности. Т.к. квадрат отрезка касательной равен произведению секущей на ее внешнюю часть, то (OK_1^2=OK_2^2=OK_3^2=OK_4^2=OBcdot OA) .

Теорема 2.

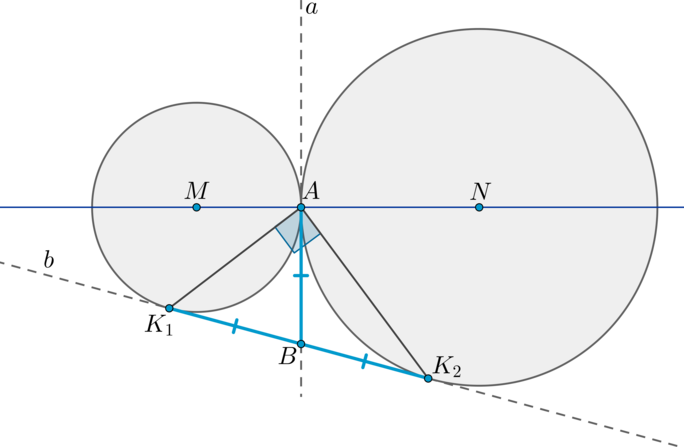
Пусть две окружности с центрами (M) и (N) касаются внешним образом в точке (A) . Две общие касательные (внутренняя и внешняя) (a) и (b) этих окружностей пересекаются в точке (B) . Точки касания — точки (A, K_1, K_2) (как показано на рисунке). Тогда [(1) <large>] [(2) <large>]

Доказательство:

1) Т.к. (BA) и (BK_1) — две касательные, проведенные к первой окружности из одной точки, то отрезки касательных равны: (BA=BK_1) . Аналогично, (BA=BK_2) . Таким образом, (BA=BK_1=BK_2) .

2) Значит, (BA) — медиана в (triangle K_1AK_2) , равная половине стороны, к которой она проведена. Значит, (angle A=90^circ) .

Теорема 3.

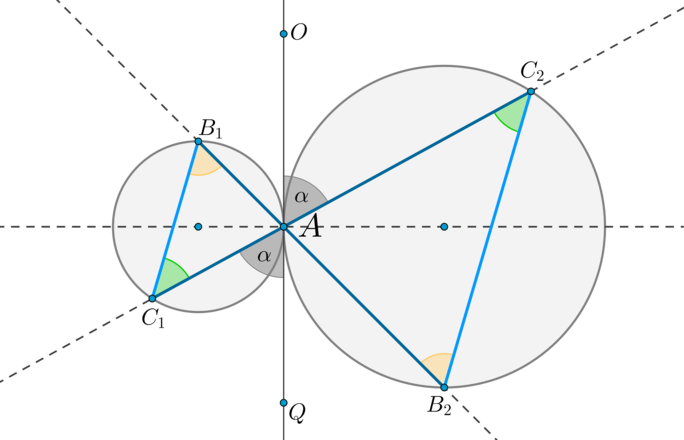
Пусть две окружности касаются внешним образом в точке (A) . Через точку (A) проведены две прямые (B_1B_2) и (C_1C_2) , пересекающие каждую окружность в двух точках, как показано на рисунке. Тогда: [(1) <large>] [(2) <large>]

Доказательство:

1) Проведем через точку (A) общую касательную этих окружностей (OQ) . (angle OAC_2=angle QAC_1=alpha) как вертикальные. Т.к. угол между касательной и хордой, проведенной через точку касания, равен половине дуги, заключенной между ними, то (angle OAC_2=frac12buildrelsmileover) , (angle QAC_1=frac12buildrelsmileover) . Следовательно, (buildrelsmileover=buildrelsmileover=2alpha) . Таким образом, (angle AB_1C_1=angle AB_2C_2=alpha) . Значит, по двум углам (triangle AB_1C_1sim triangle AB_2C_2) .

2) Т.к. (angle AB_1C_1=angle AB_2C_2) , то прямые (B_1C_1parallel B_2C_2) по накрест лежащим углам при секущей (B_1B_2) .

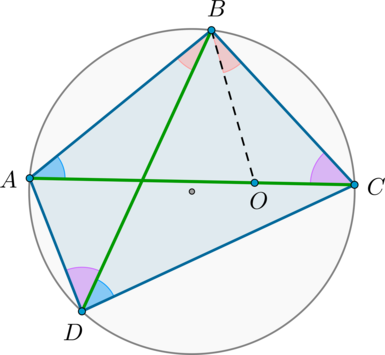
Теорема Птолемея

Во вписанном четырехугольнике произведение диагоналей равно сумме произведений противоположных сторон: [ACcdot BD=ABcdot CD+BCcdot AD]

Доказательство

Пусть для определенности (angle ABD . Проведем отрезок (BO) так, чтобы (O) лежала на (AC) и (angle ABD=angle CBO) :

Т.к. (angle ACB=angle ADB) (опираются на одну и ту же дугу), то по двум углам (triangle OBCsim triangle ABD) . Значит: [dfrac=dfrac Rightarrow ADcdot BC=OCcdot BDphantom (1)]

Т.к. (angle BAC=angle BDC) (опираются на одну и ту же дугу), (angle ABO=angle CBD) (состоят из равных по построению (оранжевых) углов и общего угла (angle DBO) ), то по двум углам (triangle ABOsim triangle BDC) . Значит: [dfrac=dfrac Rightarrow ABcdot CD=AOcdot BD phantom (2)]

Сложим равенства ((1)) и ((2)) : (ADcdot BC+ABcdot CD=OCcdot BD+AOcdot BD=ACcdot BD) , чтд.

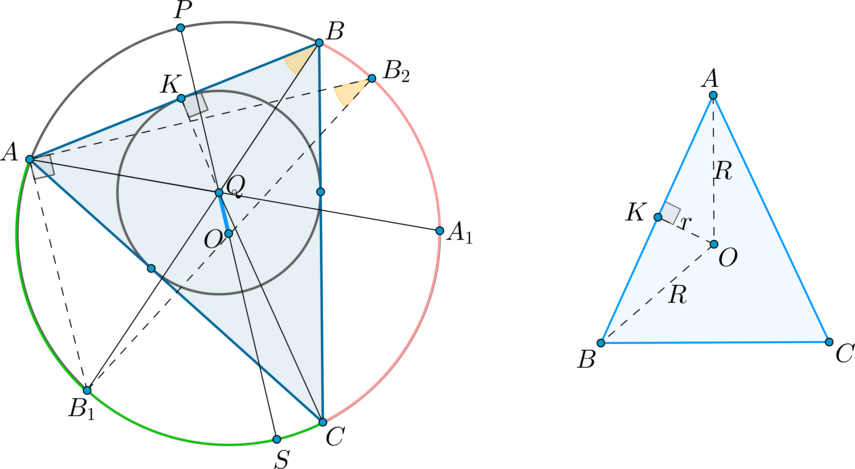
Формула Эйлера:

Пусть (R) — радиус описанной около треугольника (ABC) окружности, (r) — радиус вписанной окружности. Тогда расстояние (d) между центрами этих окружностей вычисляется по формуле: [<large>]

Доказательство:

а) Предположим, что (dne 0) . Пусть (O, Q) — центры описанной и вписанной окружности соответственно. Проведем диаметр описанной окружности (PS) через точку (Q) . Проведем также биссектрисы углов (angle A, angle B) — (AA_1, BB_1) соответственно (заметим, что они пересекутся в точке (Q) , т.к. центр вписанной окружности лежит на пересечении биссектрис). Хорды (PS) и (BB_1) пересекаются, следовательно, отрезки этих хорд равны: (PQcdot QS=BQcdot QB_1) .

Т.к. (OP=OS=R, OQ=d) , то последнее равенство можно переписать в виде ((R-d)(R+d)=BQcdot QB_1 (*)) .

Заметим, что т.к. (AA_1, BB_1) — биссектрисы, то (buildrelsmileover=buildrelsmileover=x, buildrelsmileover=buildrelsmileover=y) . Т.к. угол между хордами равен полусумме дуг, заключенных между ними, то:
(angle AQB_1=frac12(x+y)) .

С другой стороны, (angle B_1AA_1=frac12big(buildrelsmileover+buildrelsmileoverbig)=frac12(x+y))

Таким образом, (angle AQB_1=angle B_1AA_1) . Следовательно, (triangle QB_1A) — равнобедренный и (B_1Q=B_1A) . Значит, равенство ((*)) можно переписать как:
(R^2-d^2=BQcdot AB_1 (**)) .

Проведем еще один диаметр описанной окружности (B_1B_2) . Тогда (triangle B_1AB_2) — прямоугольный ( (angle A) опирается на диаметр). Пусть также вписанная окружность касается стороны (AB) в точке (K) . Тогда (triangle BKQ) — прямоугольный.
Заметим также, что (angle KBQ=angle AB_2B_1) (т.к. они опираются на одну и ту же дугу).
Значит, (triangle B_1AB_2sim triangle BKQ) по двум углам, следовательно:

(dfrac=dfrac Rightarrow dfrac=dfrac Rightarrow BQcdot AB_1=2Rr) .

Подставим это в ((**)) и получим:

(R^2-d^2=2Rr Rightarrow d^2=R^2-2Rr) .

б) Если (d=0) , т.е. центры вписанной и описанной окружностей совпадают, то (AK=BK=sqrt Rightarrow AB=2sqrt) . Аналогично (AC=BC=AB=sqrt) , т.е. треугольник равносторонний. Следовательно, (angle A=60^circ Rightarrow angle KAO=30^circ Rightarrow r=frac12R Rightarrow R=2r) или (0=R^2-2Rr) (т.е. в этом случае формула также верна).

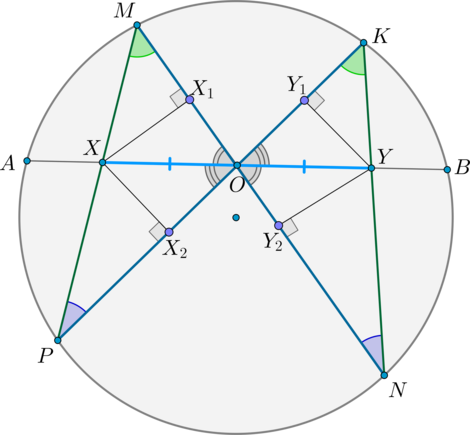
Теорема о бабочке:

Пусть через середину хорды (AB) — точку (O) , проведены две хорды (MN) и (KP) . Пусть (MPcap AB=X, KNcap AB=Y) . Тогда [<large>]

Доказательство:

Проведем перпендикуляры (XX_1, YY_2perp MN, XX_2, YY_1perp KP) .
Следующие углы равны, т.к. опираются на одну и ту же дугу: (angle PMO=angle NKO, angle MPO=angle KNO) .
Следующие углы равны, т.к. вертикальные: (angle XOX_1=angle YOY_2, angle XOX_2=angle YOY_1) .

Следующие прямоугольные треугольники подобны:

1) (triangle XX_1Osim triangle YY_2O Rightarrow dfrac=dfrac)

2) (triangle XX_2Osim triangle YY_1O Rightarrow dfrac=dfrac)

3) (triangle MXX_1sim triangle KYY_1 Rightarrow dfrac=dfrac)

4) (triangle PXX_2sim triangle NYY_2 Rightarrow dfrac=dfrac)

Из 1) и 2) следует, что

Из 3) и 4) следует, что

Совместив последние два равенства, получим:

Заметим, что для пересекающихся хорд (AB) и (MP) : (AXcdot XB=MXcdot PX) . Аналогично (AYcdot YB=KYcdot NY) . Значит:

Обозначим (OX=x, OY=y, OA=OB=t Rightarrow)

Видео:КАСАЮЩИЕСЯ ОКРУЖНОСТИСкачать

Взаимное расположение двух окружностей

Министерство образования и науки Российской Федерации

Муниципальное бюджетное общеобразовательное учреждение

города Новосибирска «Гимназия №4»

Секция: математика

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА

СВОЙСТВА ДВУХ КАСАЮЩИХСЯ ОКРУЖНОСТЕЙ

Учеников 10 класса:

Хазиахметова Радика Ильдаровича

Зубарева Евгения Владимировича

Л.Л. Баринова

Учитель математики

Высшей квалификационной категории

Содержание

§ 1.1 Взаимное расположение двух окружностей………………………. …………. ………3

§ 2 Свойства и их доказательства………………………………………..……………. ….…4

Многие задачи, включающие в себя две касающиеся окружности, можно решить более коротко и просто, зная некоторые свойства, которые будут представлены дальше.

Взаимное расположение двух окружностей

Для начала оговорим возможное взаимное расположение двух окружностей. Может быть 4 различных случая.

1.Окружности могут не пересекаться.

3. Касаться в одной точке снаружи.

4.Касаться в одной точке внутри.

§ 2. Свойства и их доказательства

Перейдем непосредственно к доказательству свойств.

Отрезки между точками пересечения касательных с окружностями равны между собой и равны двум средним геометрическим радиусов данных окружностей.

Доказательство 1. О₁А₁ и О₂В₁ – радиусы, проведённые в точки касания.

(O₁D₂=(R+r) 2 -(R-r) 2 =R 2 +2Rr+r2-R 2 +2Rr-r 2 =√4Rr=2√Rr)

А₂В₂ = 2√Rr (доказывается аналогично)

Утверждения, используемые в доказательстве 1)Проведем радиусы в точки пересечения касательных с окружностями.

2)Эти радиусы будут перпендикулярны касательным и параллельны друг другу.

3)Опустим перпендикуляр из центра меньшей окружности к радиусу большей окружности.

4)Гипотенуза полученного прямоугольного треугольника равна сумме радиусов окружностей. Катет равен их разности.

5)По теореме Пифагора получаем искомое соотношение.

Точки пересечения прямой, пересекающей точку касания окружностей и не лежащей ни в одной из них, с касательными делят пополам отрезки внешних касательных, ограниченные точками касания, на части, каждая из которых равна среднему геометрическому радиусов данных окружностей.

Доказательство 1.МС = МА₁ (как отрезки касательных)

2.МС = МВ₁ (как отрезки касательных)

Утверждения, используемые в доказательстве Отрезки касательных, проведенных из одной точки к некоторой окружности равны. Используем это свойство для обеих данных окружностей.

Длина отрезка внутренней касательной, заключенного между внешними касательными, равна длине отрезка внешней касательной между точками касания и равна двум средним геометрическим радиусов данных окружностей.

Доказательство Этот вывод следует из предыдущего свойства.

Треугольник, образованный центрами касающихся окружностей и серединой отрезка касательной между радиусами, проведенными в точки касания, прямоугольный. Отношение его катетов равно частному корней радиусов этих окружностей.

Доказательство 1.МО₁ – биссектриса угла А₁МС, МО₂ – биссектриса угла В₁МС, т.к. центр окружности, вписанной в угол лежит на биссектрисе этого угла.

2.По пункту 1 ÐО₁МС + ÐСМО₂ = 0,5(ÐА1МС + ÐСМВ₁) = 0,5p = p/2

3.ÐО₁МО₂ – прямой. МС – высота треугольника O₁МО₂, т.к. касательная МN перпендикулярна радиусам, проведённым в точки касания → треугольники О₁МС и МО₂С – подобны.

4.О₁М / МО₂ = О₁С / МС = r / √Rr = √r / R (по подобию)

Утверждения, используемые в доказательстве 1)Центр окружности, вписанной в угол, лежит на биссектрисе этого угла. Катеты треугольника являются биссектрисами углов.

2)Пользуясь тем, что образованные таким образом углы равны, получаем, что искомый рассматриваемый нами угол прямой. Делаем вывод о том, что данный треугольник действительно прямоугольный.

3)Доказываем подобие треугольников, на которые высота (так как касательная перпендикулярна радиусам, проведенным в точки касания) делит прямоугольный треугольник, и по подобию получаем искомое отношение.

Треугольник, образованный точкой касания окружностей друг с другом и точками пересечения окружностей с касательной, прямоугольный. Отношение его катетов равно частному корней радиусов этих окружностей.

1. 2α + 2β + ÐА₁МС + ÐСМВ₁ = 2p → 2α + 2β = 2p — (ÐА₁МС + ÐСМВ₁) = 2p — p = p, α + β = p/2

Утверждения, используемые в доказательстве 1)Расписываем сумму углов треугольников, пользуясь тем, что они равнобедренные. Равнобедренность треугольников доказывается при помощи свойства о равенстве отрезков касательных.

2)Расписав сумму углов таким образом, получаем, что в рассматриваемом треугольнике есть прямой угол, следовательно он прямоугольный. Первая часть утверждения доказана.

3)По подобию треугольников(при его обосновании пользуемся признаком подобия по двум углам) находим отношение катетов прямоугольного треугольника.

Четырехугольник, образованный точками пересечения окружностей с касательной, является трапецией, в которую можно вписать окружность.

2.А₁А₂ ║ В₁В₂, т.к. равны соответственные углы, образованные при пересечении секущей А₁В_1.

1. А₁В₁ + А₂В₂ = 2√Rr + 2√Rr = 4√Rr = А₁А₂ + В₁В₂ → в трапеции А₂А₁В₁В₂ сумма оснований равна сумме боковых сторон, а это является необходимым и достаточным условием существования вписанной окружности.

Утверждения, используемые в доказательстве 1)Вновь воспользуемся свойством отрезков касательных. С его помощью докажем равнобедренность треугольников, образованных точкой пересечения касательных и точками касания.

2)Из этого будет следовать подобие данных треугольников и параллельность их оснований. На этом основании делаем вывод о том, что этот четырехугольник является трапецией.

3)По доказанному нами ранее свойству(2) находим среднюю линию трапеции. Она равна двум средним геометрическим радиусов окружностей. В полученной трапеции сумма оснований равна сумме боковых сторон, а это является необходимым и достаточным условием для существования вписанной окружности.

Рассмотрим на практическом примере, как можно упростить решение задачи, используя изложенные выше свойства.

В треугольнике АВС сторона АС=15 см. В треугольник вписана окружность. Вторая окружность касается первой и сторон АВ и ВС. На стороне АВ выбрана точка F, а на стороне ВС — точка М так, что отрезок FM является общей касательной к окружностям. Найдите отношение площадей треугольника BFM и четырехугольника АFМС, если FM — 4 см, а точка М отстоит от центра одной окружности на расстояние в два раза большее, чем от центра другой.

Дано: FM-общая касательная AC=15см FM=4см O₂M=2О₁M

2)2√Rr=4, √r/R=0,5 →r=1,R=4; PQ=FM=4

Задача 2

В равнобедренный треугольник АВС вписаны две касающиеся окружности с их общей точкой Д и проходящей через эту точку общей касательной FK. Найти расстояние между центрами этих окружностей, если основание треугольника АС = 9 см, а отрезок боковой стороны треугольника заключенный между точками касания окружностей равен 4 см.

Дано: ABC – равнобедренный треугольник; FK – общая касательная вписанных окружностей. АС = 9 см; NE = 4 см

Т.к. AFKC – равнобедренная трапеция, в которую вписана окружность, то ее высота равна среднему геометрическому ее оснований, т.е. (см) .

Тогда радиус большой окружности равен 3см. Но , следовательно , тогда (см).

А расстояние между центрами окружностей в данной задаче равно (см).

Ответ: см.

Задача 3

Окружности различных радиусов r и R с центрами О₁ и О₂ соответственно касаются внешним образом в точке К. Прямая касается этих окружностей в различных точках

А и В, а вторая прямая – в точках D и C соответственно. Докажите, что ABCD – описанная трапеция и найдите ее высоту.

Пусть прямые AB и CD пересекаются в точке О. Тогда ОА = ОD, ОВ = ОС, поэтому CD = = AB = 2√Rr

Точки О₁ и О₂ лежат на биссектрисе угла AOD. Биссектриса равнобедренного треугольника AOD является его высотой, поэтому AD ┴ O₁O₂ и BC ┴ O₁O₂ , значит,

AD ║ BC и ABCD – равнобедренная трапеция.

Отрезок MN – ее средняя линия, поэтому AD + BC = 2MN = 2AB = AB + CD

Следовательно, в эту трапецию можно вписать окружность.

Пусть AP – высота трапеции, прямоугольные треугольники АРВ и О₁FO₂ подобны, поэтому АР/О₁F = АВ/О₁О₂.

Отсюда находим, что

Список литературы

• Приложение к газете «Первое сентября» «Математика» №43, 2003 год
• ЕГЭ 2010. Математика. Задача С4. Гордин Р.К.

🎬 Видео

Все об окружностях на ЕГЭ | Профильная математика 2023 | УмскулСкачать

ЕГЭ Задание 16 Две касающиеся окружностиСкачать

КАСАЮЩИЕСЯ ОКРУЖНОСТИ. # ЕГЭ 2023Скачать

Три окружности касаются прямой и друг друга внешним образомСкачать

Отрезки касательных из одной точки до точек касания окружности равны | Окружность | ГеометрияСкачать

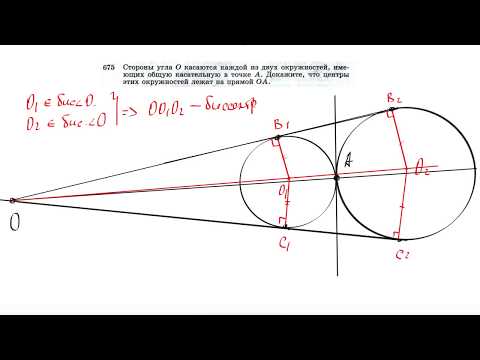
№675. Стороны угла О касаются каждой из двух окружностей, имеющих общую касательную в точке АСкачать

8 класс, 32 урок, Касательная к окружностиСкачать

9 класс, 8 урок, Взаимное расположение двух окружностейСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать

Вписанная и описанная окружность - от bezbotvyСкачать

Касательная к окружности и её свойстваСкачать

✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать