Все сечения тетраэдра треугольники

Тетраэдр — это частный случай правильной треугольной пирамиды.

Тетраэдр — правильный многогранник (четырёхгранный), имеющий 4 грани, они, в свою очередь, оказываются правильными треугольниками. У тетраэдра 4 вершины, к каждой из них сходится 3 ребра. Общее количество ребер у тетраэдра 6.

Медиана тетраэдра — это отрезок, который соединяет вершину тетраэдра и точку пересечения медиан противоположной грани (медиан равностороннего треугольника, который противолежит вершине).

Бимедиана тетраэдра — это отрезок, который соединяет середины рёбер, что скрещиваются (соединяет середины сторон треугольника, который есть одной из граней тетраэдра).

Высота тетраэдра — это отрезок, который соединяет вершину и точку противоположной грани и перпендикулярен этой грани (т.е. это высота, проведенная от всякой грани, кроме того, совпадает с центром описанной окружности).

Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

Свойства тетраэдра.

Параллельные плоскости, которые проходят через пары рёбер тетраэдра, что скрещиваются, и определяют описанный параллелепипед около тетраэдра.

Плоскость, которая проходит сквозь середины 2-х рёбер тетраэдра, что скрещиваются, и делит его на 2 части, одинаковые по объему.

Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, если считать от вершины. Она же делит бимедианы на две равные части.

Видео:ПОСТРОЕНИЕ СЕЧЕНИЙ ТЕТРАЭДРА ПЛОСКОСТЬЮСкачать

Типы тетраэдров.

Правильный тетраэдр — это такая правильная треугольная пирамида, каждая из граней которой оказывается равносторонним треугольником.

У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину.

Тетраэдр состоит из 4 граней, 4 вершин и 6 ребер.

Правильный тетраэдр — это один из 5-ти правильных многогранников.

Кроме правильного тетраэдра, заслуживают внимания такие типы тетраэдров:

— Равногранный тетраэдр, у него каждая грань представляет собой треугольник. Все грани-треугольники такого тетраэдра равны.

— Ортоцентрический тетраэдр, у него каждая высота, опущенная из вершин на противоположную грань, пересекается с остальными в одной точке.

— Прямоугольный тетраэдр, у него каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине.

— Каркасный тетраэдр — тетраэдр, который таким условиям:

• есть сфера, которая касается каждого ребра,
• суммы длин ребер, что скрещиваются равны,
• суммы двугранных углов при противоположных ребрах равны,
• окружности, которые вписаны в грани, попарно касаются,
• каждый четырехугольник, образующийся на развертке тетраэдра, — описанный,
• перпендикуляры, поставленные к граням из центров окружностей, в них вписанных, пересекаются в одной точке.

— Соразмерный тетраэдр, бивысоты у него одинаковы.

— Инцентрический тетраэдр, у него отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке.

Видео:Как строить сечения тетраэдра и пирамидыСкачать

Формулы для определения элементов тетраэдра.

Высота тетраэдра:

где h — высота тетраэдра, a — ребро тетраэдра.

Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.

где V — объем тетраэдра, a — ребро тетраэдра.

Основные формулы для правильного тетраэдра:

Где S — Площадь поверхности правильного тетраэдра;

h — высота, опущенная на основание;

r — радиус вписанной в тетраэдр окружности;

Видео:Сечение тетраэдра? Легко! (в помощь студенту)Скачать

Тетраэдр

Древние греки дали многограннику имя по числу граней. «Тетра» означает четыре, «хедра» — означает грань (тетраэдр – четырехгранник).

Видео:ЕГЭ профиль: сечения часть 1Скачать

Поэтому на вопрос — «что такое тетраэдр?», можно дать следующее определение: » Тетраэдр это геометрическое тело из четырех граней, каждая их которых — правильный треугольник «.

Многогранник относится к правильным многогранникам и является одним из пяти Платоновых тел .

Тетраэдр имеет следующие характеристики:

• Тип грани – правильный треугольник;
• Число сторон у грани – 3;
• Общее число граней – 4;
• Число рёбер, примыкающих к вершине – 3;
• Общее число вершин – 4;
• Общее число рёбер – 6;

Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180°.
Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.

Является ли тетраэдр пирамидой? Да, тетраэдр это треугольная пирамида у которой все стороны равны.

Может ли пирамида быть тетраэдром? Только если это пирамида с треугольным основанием и каждая из её сторон равносторонний треугольник.

Отметим, что очень редко, но встречаются геометрические тела, составленные не из правильных треугольников, и их тоже называют тетраэдры, так как они имеют четыре грани.

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Математические характеристики тетраэдра

Тетраэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.

Радиус описанной сферы тетраэдра определяется по формуле:

, где a — длина стороны.

Сфера может быть вписана внутрь тетраэдра.

Радиус вписанной сферы тетраэдра определяется по формуле:

Площадь поверхности тетраэдра

Для наглядности, площадь поверхности тетраэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон тетраэдра (это площадь правильного треугольника) умноженной на 4. Либо воспользоваться формулой:

Объем тетраэдра определяется по следующей формуле:

Высота тетраэдра определяется по следующей формуле:

Расстояние до центра основания тетраэдра определяется по формуле:

Видео:Геометрия. Как строить сечения в тетраэдре.Скачать

Вариант развертки

Тетраэдр можно изготовить самостоятельно. Бумага или картон самый подходящий вариант. Для сборки потребуется бумажная развёртка — единая деталь с линиями сгибов.

Древнегреческий философ Платон ассоциировал тетраэдр с «земным» элементом огонь, поэтому для построения модели этого правильного многогранника мы выбрали красный цвет.

Заметим, что это не единственный вариант развертки.

Для построения модели Вы можете скачать развертку в формате pdf и распечатать на листе формата А4:
— если Вы предполагаете распечатать на цветном принтере — цветная развертка
— если Вы предполагаете использовать для сборки цветной картон — развертка

Видео:КАК ПОСТРОИТЬ СЕЧЕНИЕ ТЕТРАЭДРА? #математика #егэматематика #математикапрофильСкачать

Видео. Тетраэдр из набора «Волшебные грани»

Вы можете изготовить модель тетраэдра воспользовавшись деталями для сборки из набора «Волшебные грани».

Сборка многогранника из набора:

Подробная сборка от Алексея Жигулева (youtube-канал PRO)

Подробная сборка от Алексея Жигулева (youtube-канал PRO)

вращение готового многогранника:

Видео:Как строить сеченияСкачать

Видео. Вращение всех правильных многогранников

Популярное

Под руководством учителя математики Тимофеевой Татьяны Юрьевны ребята работали над проектом «Удивительный мир многогранников». Делали свои развертки и использовали развертки из.

Найти подарок для школьника, который будет интересным, полезным, а также не разорит семейный бюджет – возможно ли такое в 2020 году? Рассказываем, чем можно.

Современный кинематограф постарался привлечь внимание зрителя, используя геометрические формы «инопланетного происхождения».

Интересный лайфхак, прислала наша читательница из Республики Беларусь.

Что будет, если плоскую геометрическую фигуру, например прямоугольник, начать быстро вращать относительно одной из его сторон? Одним лишь вращением мы можем.

Нечасто удается встретить многогранники за пределами учебников математики. И если такие геометрические формы как куб, призма и цилиндр встречаются повседневно, то.

Существует концепция, что вершина многогранника отдает энергию, а плоскость энергию принимает. В том случае, если в многограннике вершин больше чем плоскостей, то он обладает.

Видео:10 класс, 12 урок, ТетраэдрСкачать

Тетраэдр и его сечения. 10-й класс

Класс: 10

Презентация к уроку

Загрузить презентацию (377 кБ)

Цели урока:

1. Ввести понятие тетраэдра и его составляющих,
2. Научить изображать тетраэдр,
3. Сформировать навык применения аксиом стереометрии и их следствий,
4. Ввести определение сечения и правила построения сечений
5. Развивать пространственное мышление , умение работать с компьютером
6. Воспитывать стремление к приобретению новых знаний, интерес к предмету
7. Обосновывать и опровергать выдвигаемые предложения.

Видео:Тетраэдр. 10 класс.Скачать

Ход урока

Актуализация знаний

Здравствуйте ребята. (показываю тетраэдр) Сегодня я познакомлю вас с геометрической фигурой, которая называется тетраэдр.

СЛАЙД №1. Тетраэдр – означает четырехгранник,( τετραεδρον) «tetra»- по -гречески четыре, а «hedra» -грань.

СЛАЙД №2. Рассмотрим произвольный треугольник АВС и точку D, не лежащую в плоскости этого треугольника. Соединив точку D отрезками с вершинами треугольника АВС получим треугольники DАВ, DВС, DСА. Поверхность, составленная из четырех треугольников АВС, DАВ, DВС, DСА, называется тетраэдром и обозначается DАВС.

Слайд №3. Тетраэдр изображается обычно в виде выпуклого и невыпуклого четырехугольника с диагоналями. При этом штриховыми линиями изображаются невидимые ребра

Начертите по образцу тетраэдр в тетради, обозначьте их, оба способа.

Слайд №4,5. Треугольники, из которых состоит тетраэдр, называются его гранями,

стороны граней — ребрами, вершины граней — вершинами тетраэдра.

Два ребра тетраэдра, не имеющие общих вершин, называются противоположными. Два ребра тетраэдра, не имеющие общих вершин, называются противоположными.

Назовите , пожалуйста, противоположные ребра тетраэдра DАВС.

ВЫПОЛНИМ ЗАДАНИЕ №66 УЧЕБНИК страница 29

Слайд №6. Правильный тетраэдр – правильный четырехгранник, то есть тетраэдр с равными ребрами, представляет собой правильный многогранник, все грани которого – правильные треугольники и из каждой вершины которого выходит ровно три ребра.

Прежде чем приступить к следующему новому для вас определению вспомним и применим знания аксиом стереометрии для решения следующего теста .

1. Если две плоскости имеют общую точку, то

• А) они называются пересекающимися,
• Б) они пересекаются по прямой, проходящей через эту точку,
• В) они параллельны

2. Через прямую и не лежащую на ней точку

• А) проходит плоскость и при том только одна
• Б) проходит бесконечно много плоскостей
• В) нельзя провести плоскость

3. Две прямые называются скрещивающимися, если

• А) они лежат в одной плоскости и не пересекаются
• Б) они не пересекаются
• В) они не пересекаются и не параллельны

4. Если прямая пересекает две параллельные прямые, то

• А) она пересекает плоскость, образованную этими параллельными прямыми
• Б) она параллельна плоскости, образованными этими прямыми
• В) она лежит в плоскости, определенными этими параллельными прямыми

5. Если две прямые параллельны третьей, то

• А) они лежат в одной плоскости
• Б) они параллельны
• В) они скрещивающиеся.

Слайд №9. сверяем ответы. 1А, 2А, 3В, 4В, 5Б. (обосновываем, опровергаем ).

Изучение нового материала

СЕКУЩЕЙ ПЛОСКОСТЬЮ ТЕТРАЭДРА НАЗЫВАЕТСЯ ЛЮБАЯ ПЛОСКОСТЬ , ПО ОБЕ СТОРОНЫ ОТ КОТОРОЙ ИМЕЮТСЯ ТОЧКИ ДАННОГО ТЕТРАЭДРА.

СЕКУЩАЯ ПЛОСКОСТЬ ПЕРЕСЕКАЕТ ГРАНИ ТЕТРАЭДРА ПО ОТРЕЗКАМ. МНОГОУГОЛЬНИК, СТОРОНАМИ КОТОРОГО ЯВЛЯЮТСЯ ЭТИ ОТРЕЗКИ, НАЗЫВАЕТСЯ СЕЧЕНИЕМ ТЕТРАЭДРА.

Слайд № 11. Правила построения сечений ТЕТРАЭДРА:

1. проводим прямые через точки, лежащие в одной плоскости;
2. ищем прямые пересечения плоскости сечения с гранями многогранника, для этого
   а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);
   б) параллельные грани плоскость сечения пересекает по параллельным прямым.

И так сечение, что же это такое?

Усвоение нового понятия

Закрепление

Слайды №15 задание на построение сечений.

Слайд №16. взаимопроверка .

Домашнее задание № 67, №71. § 12, § 14 (1 абзац).

Итоги урока:

Чем занимались на уроке?
С чем познакомились?
Как построить сечение тетраэдра?
Что понравилось? Что не понравилось?

🎥 Видео

СЕЧЕНИЯ ТЕТРАЭДРА И ПАРАЛЛЕЛЕПИПЕДАСкачать

ВСЕ О СЕЧЕНИЯХ В СТЕРЕОМЕТРИИСкачать

Геометрия 10.Тетраэдр (теория, сечение тетраэдра)Скачать

Построение сечений тетраэдраСкачать

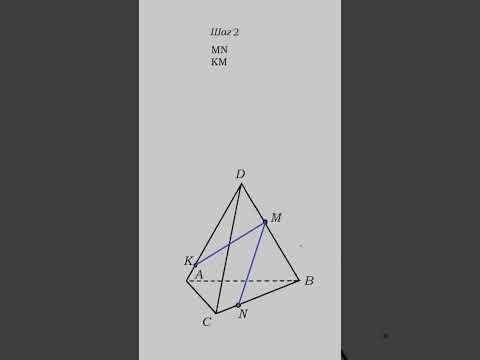
№74. Через точку пересечения медиан грани BCD тетраэдра ABCD проведена плоскостьСкачать

Как строить сечения параллелепипедаСкачать

Развертка тетраэдра - это легко! Как сделать объёмную правильную треугольную пирамиду из бумаги?Скачать

14. Задачи на построение сеченийСкачать

ТЕТРАЭДР 10 класс стереометрия сечение тетраэдраСкачать