Какое из следующих утверждений верно?
1) Все равнобедренные треугольники подобны.
2) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
3) Сумма углов прямоугольного треугольника равна 90 градусам.
Проверим каждое из утверждений.
1) «Все равнобедренные треугольники подобны.» — неверно, не все равнобедренные треугольники подобны.
2) «Существует прямоугольник, диагонали которого взаимно перпендикулярны.» — верно, такой прямоугольник — это квадрат.
3) «Сумма углов прямоугольного треугольника равна 90 градусам.» — неверно, сумма острых углов прямоугольного треугольника равна 90 градусам.
Видео:Все равнобедренные треугольники подобны. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Все равнобедренные прямоугольные треугольники подобны
Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Источник задания: Решение 2555. ОГЭ 2018 Математика, И.В. Ященко. 36 вариантов.
Задание 20. Какое из следующих утверждений верно?
1) Все равнобедренные треугольники подобны.
2) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
3) Сумма углов прямоугольного треугольника равна 90 градусам.
1) Нет, из условий подобия следует, что все стороны и углы треугольников пропорционально больше или меньше друг друга.
2) Да, диагонали взаимно перпендикулярны у квадрата, это частный случай прямоугольника.
3) Нет, сумма углов в любом треугольнике 180 градусов.
Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Три признака подобия треугольников
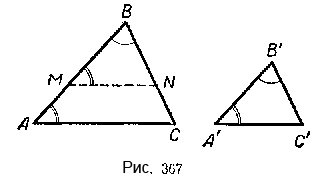
Теорема 1. Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.
Пусть в треугольниках ABC и А’В’С ∠A = ∠А’ ∠В = ∠B’ (в подобных треугольниках вершины соответственно равных углов часто обозначают одинаковыми буквами).
Доказать, что (Delta)ABС (sim) (Delta)А’В’С (рис. 367).
Прежде всего отметим, что из равенства двух углов данных треугольников следует, что и третьи углы их равны, т. е. ∠C = ∠С’.
Отложим от вершины В, например, на стороне AB треугольника ABC отрезок ВМ, равный отрезку А’В’. Из точки М проведём прямую MN || АС. Мы получили (Delta)MBN, который подобен (Delta)ABC. Но (Delta)MBN = (Delta)А’В’С’, так как ∠В = ∠В’ по условию теоремы; сторона MB = A’B’ по построению; ∠BMN = ∠A’ (∠BMN и ∠А’ порознь равны одному и тому же ∠А).
Если (Delta)MBN (sim) (Delta)AВС, то (Delta)А’В’С’ (sim) (Delta)ABC. Эта теорема выражает 1-й признак подобия треугольников.
Следствия. 1. Равносторонние треугольники подобны.
2. Равнобедренные треугольники подобны, если они имеют по равному углу при вершине или при основании.
3. Два прямоугольных треугольника подобны, если она имеют по равному острому углу.
4. Равнобедренные прямоугольные треугольники подобны.
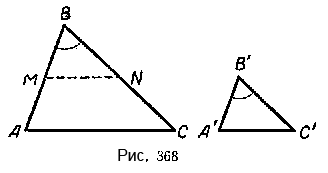
Теорема 2 . Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, лежащие между ними, равны.
Пусть в треугольниках ABC и А’В’С’ (frac = frac) и ∠В = ∠В’
Требуется доказать, что (Delta)ABC (sim) (Delta)А’В’С’ (рис. 368).
Для доказательства отложим, например, на стороне AB треугольника ABC от вершины В отрезок ВМ, равный отрезку А’В’. Через точку М проведём прямую MN || АС. Полученный треугольник MBN подобен треугольнику ABC.
Докажем, что (Delta)MBN = (Delta)А’В’С’. В этих треугольниках ∠В = ∠В’ по условию теоремы, MB = А’В’ по построению. Чтобы убедиться в равенстве сторон BN и В’С, составим пропорцию AB /MB = BC /BN (она вытекает из параллельности АС и MN) и сравним её с пропорцией, которая дана в условии теоремы: (frac = frac). В этих двух пропорциях имеется по три равных члена, следовательно, равны и четвёртые их члены,
т. е. В’С’ = BN. Отсюда следует равенство треугольников MBN и А’В’С’.
Так как (Delta)MBN (sim) (Delta)А’В’С’, то, следовательно, и (Delta)А’В’С’ (sim) (Delta)ABС.
Эта теорема выражает 2-й признак подобия треугольников.
Следствие. Прямоугольные треугольники подобны, если катеты одного из них пропорциональны катетам другого.
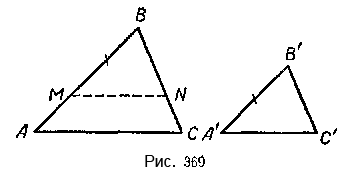
Теорема 3. Два треугольника подобны, если три стороны одного треугольника пропорциональны трём сторонам другого треугольника.
Пусть в треугольниках ABC и А’В’С’ (frac = frac = frac) (рис. 369).
Требуется доказать, что (Delta)ABC (sim) (Delta)А’В’С’
Для доказательства отложим на стороне AB треугольника ABC от вершины В отрезок BM = А’В’. Из точки M проведём прямую MN || АС. Полученный треугольник MBN подобен треугольнику ABC. Следовательно, (frac = frac = frac).
Докажем, что (Delta)MBN = (Delta)А’В’С’. Для доказательства сравним две пропорции
(frac = frac) и (frac = frac).
В этих пропорциях имеется по три равных члена, следовательно, равны и четвёртые их члены, т.е. BN = В’С’.
Сравним ещё две пропорции: (frac = frac) и (frac = frac) . В этих пропорциях также имеется по три равных члена, следовательно, равны и четвёртые члены их, т. е. MN =А’С’.
Оказалось, что три стороны (Delta)BMN равны трём сторонам (Delta)А’В’С’, а именно:
MB = А’В’, BN = В’С’ и MN = А’С’.
Следовательно, (Delta)MBN = (Delta)А’В’С’, а (Delta)ABC (sim) (Delta)А’В’С’.
Эта теорема выражает 3-й признак подобия треугольников.
🎬 Видео
Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Свойства прямоугольного треугольника. 7 класс.Скачать

Все прямоугольные треугольники равнобедренные!?!?#егэ2023 #егэ #математика #геометрия #школа #fypСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Подобие в прямоугольных треугольникахСкачать
Равнобедренный треугольник. 7 класс.Скачать

Особенные прямоугольные треугольники, часть 1 (видео 25) | Подобие. Геометрия | МатематикаСкачать

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК §17 геометрия 7 классСкачать

Найдите сторону треугольника на рисункеСкачать

Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Всё про прямоугольный треугольник за 15 минут | Осторожно, спойлер! | Борис Трушин !Скачать

Теорема ПифагораСкачать

№254. Найдите углы равнобедренного прямоугольного треугольника.Скачать

135 Равнобедренный прямоугольный треугольник, проекция которого подобна ему (решение)Скачать

Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Подобие прямоугольных треугольников и его применениеСкачать