Объем вращения прямоугольного треугольника

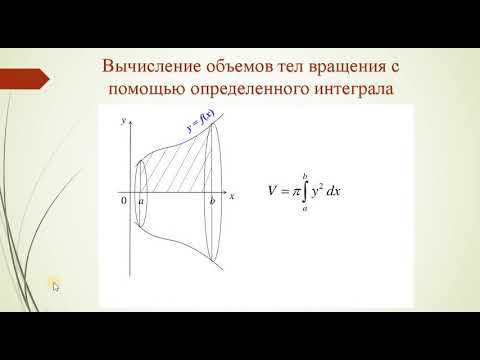
В данной методической разработке приведены формулы и разобраны примеры решения традиционных задач на вычисление объёмов тел вращения. Эта разработка предназначена для студентов СПО, находящихся на дистанционной форме обучения. Также эта работа может быть полезна преподавателям математики учреждений системы СПО для организации подготовки студентов к контрольной работе по данной теме.

Видео:Интегралы №13 Объем тела вращенияСкачать

Скачать:

Видео:Лекция 1. Точка на прямой. Метод прямоугольного треугольникаСкачать

Предварительный просмотр:

Тема. «Объёмы тел вращения».

Методическое пособие по решению задач для студентов 2 курса СПО.

Дистанционная форма обучения.

1. Теоретический материал.

Вид круглого тела

V = R 2 H

V = R 2 H

3. Усеченный конус

V = h(R 2 + Rr + r 2 )

V = R 3

2. Решение задач.

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 36 см 3 .

R ц = R к = R; H ц = H к = H;

V ц = R 2 H; V к = R 2 H,

следовательно объем цилиндра в 3 раза больше

V ц =

Высота одного цилиндра вдвое больше высоты второго цилиндра, но его радиус в два раза меньше радиуса второго цилиндра. Найти отношение их объёмов

R 1ц = R; Н 1ц = Н; R 2ц = 2R;

Н 2ц = Н;

Найти:

V 1ц = R 2 H;

V 1ц =

=

Ответ. =

Найти объем 25м цилиндрической трубы (полого цилиндра), если внешний радиус равен 50см, диаметр стенок равен 10см.

Дано: полый цилиндр;

R = 50cм = 0,5м; d = 10см = 0,1м

V = Н(R 2 — r 2 ); r = R — d; r = 0,5 — 0,1 = 0,4(м)

Ответ. 2,25 м 3

Объём конуса равен 36 , а его высота равна 12. Найдите радиус основания конуса.

Н=12; V = 36

V к = R 2 H; 36 = ; 4 R 2 =36 ;

4R 2 =36; R 2 = 36:4 = 9; R = =3

Объем конуса равен 24 см 3 . Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной.

Найдите объем меньшего конуса.

V б к = 24см 3 ; SA = SO

Так как SA = SO, то два конуса подобны.

Коэффициент подобия к =2, следовательно

; ; 8 V м к = 24; V м к = 24:8=3

V б к = R 2 SO V м к = r 2 SA ; R = 2r; SO=2SA

; ;

8 V м к = 24; V м к = 24:8=3

Диаметр основания конуса равен 16, а длина образующей — 17. Найдите объем конуса.

Дано: конус, D =16; L = 17

V к = R 2 H;

SAO — прямоугольный, так как SO — высота

конуса, по теореме Пифагора найдем Н.

R = D=8(см)

Н 2 = L 2 — R 2 ; Н 2 = 17 2 = 8 2 =289-64=225;

Н = =15;

V к =

Ответ.320

Радиусы оснований усечённого конуса равны 4 и 12, а образующая равна 10. Вычислить объем усечённого конуса.

Дано: усеченный конус;

V = h(R 2 + Rr + r 2 )

Высоту усеченного конуса найдем из прямоугольного треугольника АВС (АВ провели параллельно h )

АВ 2 = АС 2 — ВС 2 ; ВС=R-r=12-4=8

АВ 2 = 10 2 — 8 2 =100-64=36; АВ=6; h=6

V =

Ответ. 416

Видео:Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Внутренний диаметр полого шара равен 8 см, а толщина стенок равна 2 см. Найдите объем материала, из которого сделан шар.

СD = 8см; АС = 2см

Рассмотрим сечение полого шара диаметральной плоскостью.

Видео:5 класс, 21 урок, Объемы. Объем прямоугольного параллелепипедаСкачать

V=V 1 — V 2 ; V 1 = R 3 ; V 2 = r 3 ; r= СD; R= r +AC

r= СD = (см); R= 4 +2 = 6(см)

Ответ.

Прямоугольная трапеция с основаниями 11см и 17 см и высотой 12 см вращается около прямой, проходящей через вершину острого угла перпендикулярно основаниям. Hайдите объем полученного тела вращения.

Дано: АВСD — трапеция; ВAD=90 0 ; ВС=11см; AD=17 см;

Найти: V тела вращения

При вращении трапеции ABCD получим цилиндр, радиус его основания R = AD =17 см, высотой Н = AB =12 см,

из которого вырезан конус с радиусом основания

r =17-11=6 см, высота h=AB=12 см.
V т.вр. = V цил. — V кон

V цил = R 2 H; V цил = ;

V кон = ; V кон =

V т.вр = 3468 -144 =3468 = 3324 (см 3 )

Ответ. 3324 см 3

Прямоугольный треугольник с катетами 20 см и 15 см вращается вокруг гипотенузы . Найти объём полученного тела вращения.

Дано: АВС — прямоугольный,

С = 90 0 ;

АС=15 см; ВС = 20 см.

Найти: V тела вращения

При вращении прямоугольного треугольника АВС

вокруг гипотенузы получается тело вращения, состоящее из двух конусов с общим основанием.

Радиус R этого основания есть перпендикуляр СО, опущенный из вершины прямого угла на гипотенузу.

V т.вр. = V 1 кон. + V 2 кон ;

V 1 кон. = ; V 2 кон. =

V т.вр. =

По теореме Пифагора найдем гипотенузу АВ

АВ 2 =АС 2 +ВС 2 ; АВ 2 =15 2 +20 2 =225+400=625;

АВ= =25 см

Чтобы найти R, из треугольника АВС определим

sin A= ; sin A= ;

Из прямоугольного треугольника АОС

sin A= ; ; ОС= (см); R=12 см

V т.вр =

Ответ. 1200 см 3

Задания для самостоятельного решения.

1. Даны две кружки цилиндрической формы. Первая кружка в полтора раза ниже второй, а вторая вдвое шире первой. Во сколько раз объём второй кружки больше объёма первой?

2. Однородный шар диаметром 3 см имеет массу 162 грамма. Чему равна масса шара, изготовленного из того же материала, с диаметром 2 см? Ответ дайте в граммах.

3. Осевое сечение конуса равносторонний треугольник, сторона которого равна 12 см. Найдите объём конуса.

4. Найти объем тела, полученного в результате вращения прямоугольного треугольника вокруг гипотенузы, если катеты равны 3см и 4 см.

Видео:Нахождение натуральной величины отрезка методом прямоугольного треугольникаСкачать

5. Прямоугольная трапеция с основанием 5 см и 8 см и высотой 4 см вращается около

Видео:Математика | Объём в жизни и в математикеСкачать

большего основания. Найдите объем тела вращения.

Видео:Математика 5 Объем Объем прямоугольного параллелепипедаСкачать

Тема: «Решение задач на вычисление объемов тел вращения.»

Предмет, класс: «Геометрия», 11«б» класс.

(класс с углубленным изучением математики)

Тема: «Решение задач на вычисление объемов тел вращения.»

Программа: Программы для общеобразовательных

школ, гимназий, лицеев. Математика.5-11 кл. – М., «Просвещение», 2006.

Тип урока: урок применения знаний и умений.

Педагогический стаж: 33года

Стаж работы учителем: 33года

Дата выполнения: апель 2008 года

Психолого-педагогическая характеристика класса.

В 11 «б» классе обучается 18 человек: 4 мальчика, 14девочек.

15 детей относится к основной группе здоровья, 3 относятся к подготовительной. Полных семей-17, в 1-ой семье нет отца (развод).

Все ученики коммуникативно развиты, охотно общаются друг с другом, дружат. Межличностные отношения в классе нормальные, они, в целом, основаны на дружбе, товариществе, уважении друг к другу, готовности оказать помощь однокласснику. Ребята чувствуют себя полноправными членами коллектива. Результаты социометрии показали, что в классе «непредпочитаемых» ребят нет. В числе «принятых» все. К учителям относится с уважением, обстановка на уроках рабочая. Ученики хорошо знают свои возможности и возможности своих товарищей, умело распределяют работу при групповых заданиях, при необходимости готовы оказать помощь друг другу.

Успеваемость по итогам I полугодия выглядит следующим образом: на «5» учится 2 человека, на «4» и «5» — 15 человек, из них 3-ое с одной «4» и двое с двумя «4», 1 человек — с одной «3».

По своему развитию к группе высокого уровня развития можно отнести 10 учеников. Ее характеризует устойчивое положительное отношение к познавательной задаче, осознанное стремление к правильному ее решению. Ученики способны легко принимать задачу и удерживать ее, переключаться на другие виды работы. Задания выполняют самостоятельно. Внимание у этих детей произвольное, объем, концентрация и устойчивость достаточно высокие, уровень мотивации к учению – высокий. Они быстро усваивают материал. У учащихся развита наблюдательность. Умение видеть и выделять существенные признаки. Сравнивать. Находить различия, обобщать. Эти ученики отвечают на вопросы. Умеют рассказывать, у них хорошо развита речь и память (зрительная, слуховая, моторная, логическая), словарный запас большой, присутствует эмоциональная окраска. Присутствует практическое, образное, логическое мышление. Любят читать. Хорошо развит практический интерес. Они уравновешенны, способны к волевому усилию, соблюдают правила поведения, любят учиться. У этих детей высокий самоконтроль, способность быстро сосредоточиться, планировать свои дела и доводить их до конца.

К группе среднего развития относятся 8 человек. Внимание у них произвольное, объем концентрации и устойчивость средние. Хорошо развита зрительная и слуховая память, хотя преобладает механическая. Усвоение нового материала занимает больше времени, чем для первой группы. Определения, выводы и понятия для запоминания требуется повторить несколько раз. В большинстве случаев они могут самостоятельно установить причинно-следственные связи, проанализировать событие или факт. Однако для успешного выполнения данного рода заданий им нередко требуется помощь более сильного ученика или учителя. Практическое мышление преобладает над образным. Речь хорошо развита. Однако наиболее успешно им даются ответы воспроизводящего характера. Творческие задания нередко вызывают затруднения. Учебный материал усваивают хорошо. В поведении уравновешены, способны к волевому усилию.

Учащихся с низким уровнем развития нет.

Тема, цели, оборудование урока.

Тема урока: «Решение задач на вычисление объемов тел вращения.»

Образовательная-сформировать умения решать задачи на вычисление объема комбинации тел вращения.

Развивающая —развивать познавательный интерес учащихся в процессе решения задач повышенной сложности и умения преодолевать трудности при их решении.

Воспитательная – воспитывать волю и настойчивость в достижении цели.

Оборудование урока: мультимедийная установка, раздаточный материал (тексты задач для самостоятельной и домашней работ, тесты).

1.Постановка цели урока и мотивация учебной деятельности учащихся.(2 минуты)

2.Воспроизведение опорных знаний.(10 минут)

3.Осмысление содержания и последовательности применения практических действий при выполнении предстоящих заданий.

4.Самостоятельное выполнение учащимися заданий.(10 минут)

5.Презентация выполненных заданий и их обсуждение.(15 минут)

6. Подведение итогов урока и постановка домашнего задания.

1.Постановка цели и мотивация учебной деятельности.

-Какую тему мы изучаем? (Объемы тел)

-Объемы каких тел мы научились находить? (Объемы: прямой и наклонной призм ; пирамиды и усеченной пирамиды ;цилиндра, конуса и усеченного конуса; шара, шарового сегмента, шарового слоя и шарового сектора. )

-Какие из этих тел являются телами вращения? (Цилиндр, конус, усеченный конус, шар, шаровой сектор.)

–Цель урока — научиться решать задачи на вычисление объемов тел вращения, которые будут являться комбинацией основных тел вращения.

Такие задачи часто предлагаются на вступительных экзаменах в вузы.(Объявляется тема урока.)

2. .Воспроизведение опорных знаний.

-Вспомним, как получаются тела вращения и каковы формулы для вычисления их объемов и площадей поверхностей.

(Учащиеся дают определения телам вращения, называют формулы для вычисления объемов и площадей поверхностей тел. В это время на экране появляются изображения этих тел и формулы.)

Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон.

—Конус может быть получен вращением прямоугольного треугольника вокруг одного из катетов, при этом боковая поверхность образуется вращением гипотенузы, а основание вращением другого катета.

-Усеченный конус может быть получен вращением прямоугольной трапеции вокруг его боковой стороны, перпендикулярной к основанию, при этом боковая поверхность получается вращением другой боковой стороны, а основания усеченного конуса — вращением оснований трапеции.

или

–Сфера получается вращением полуокружности вокруг диаметра. Тело ограниченное сферой называется шаром

Проверим умения применять формулы объемов и площадей поверхностей тел вращения к решению задач с помощью теста.

-Тест. (Приложение ) Ответы: 1 вариант 2 вариант

(Ответы сдаются на проверку, а по 2-ому варианту ответов учащиеся оценивают свою работу )

3.Осмысление содержания и последовательности применения практических действий при выполнении предстоящих заданий.

-Задачи на вычисление объемов тел вращения делятся на два типа:

1) задачи, в которых тела вращения образуются в процессе решения;

2) задачи, в которых тела вращения не образуются в процессе решения, а даны изначально.

-Какие задачи из теста можно отнести к задачам 1-ого типа, а какие к задачам 2-ого типа? (3-я задача 2-ого типа, а остальные 1-ого )

-Задачи 2-ого типа мы решали и при изучении темы «Площади поверхностей тел вращения», поэтому задачи на вычисление объемов таких комбинаций я предложу вам в домашнем задании.

-Рассмотрим задачи 1-го типа из теста.

-Чем отличаются первые три задачи от задачи 5-ой? (В 5-ой задаче надо было применить свойства объемов)

(Равные тела имеют равные объемы. Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел.)

-Вот сегодня на уроке мы и будем решать такие задачи 1-ого типа, в которых надо не только применять формулы для вычисления объемов тел вращения, но и свойства объемов. Но в отличии от задач из теста, в них не будут известны элементы фигур вращения, потребуется вводить обозначения, делать преобразования, чтобы выразить искомый объем через данные задачи.

Задачи, которые будут предлагаться вам сегодня на уроке, взяты из заданий вступительных экзаменов в НГУ им. разных лет.

-Рассмотрим 1-ую задачу и обсудим алгоритм решения таких задач.

Объемы тел, получающихся при вращении прямоугольника АВСD вокруг сторон АВ и АD, равны, соответственно, 1 и . Найдите объем тела, получающегося при вращении этого прямоугольника вокруг прямой, проходящей через вершину А и перпендикулярной диагонали АС.

1)Выразить объем искомой фигуры через объемы основных тел вращения, используя свойства объемов;

2)Ввести обозначения, через которые выразить объемы тех тел, для которых даны значения объемов и объем искомого тела;

3)Получив выражение для объема искомого тела, с помощью введенных обозначений, стремиться с помощью преобразований выразить его через данные объемы тел вращения для получения значения искомого объема.

Решение: (поэтапно появляется на экране)

1) Пусть на рисунке ВМ, АС, DN перпендикулярны MN. Тогда искомый объем есть , где и .

2)Положим далее АС=d, , тогда , и МВ=dsin, ND=dcos, AM=AN=dsincos. После преобразований получается, что .

При вращении прямоугольника вокруг его сторон получаются цилиндры, их объемы суть и .

3)Поскольку и , то и при , находим, что V=2.

4.Самостоятельное выполнение учащимися заданий.

Класс разбивается на 4 группы. Каждой группе предлагается решить задачу 1-го типа, а затем представить свое решение для обсуждения.

Задача 1 ( для 1-ой и 3-ей группы):

Объемы тел, получающихся при вращении ромба вокруг каждой из его диагоналей, равны, соответственно, 1 и . Найдите объем тела, получающегося при вращении ромба вокруг его стороны.

Задача 2( для 2-ой и 4-ой группы):

Через вершины А, В и С прямоугольного треугольника АВС, в котором=, проведены прямые m‌||ВС, n ||AC, p|| AB. Объемы тел, получающихся при вращении треугольника АВС вокруг прямых m и n, равны, соответственно, 65 и 156. Найдите объем тела, получающегося при вращении этого треугольника вокруг прямой p.

5.Презентация выполненных заданий и их обсуждение.

Решение 1-ой задачи :

Пусть ABCD – данный ромб, положим АВ=а и .

Тогда АО=а cos, ВО=а sin и объем тела, получающегося при вращении ромба вокруг диагонали АС, есть . Аналогично, объем тела, получающегося при вращении ромба вокруг диагонали BD, есть . При нахождении объема тела V, получающегося при вращении ромба вокруг его стороны (например АВ на рисунке 2) надо к объему цилиндра, образованного вращением прямоугольника MNCD, прибавать объем конуса, образованного вращением треугольника AMD, и вычесть объем конуса, образованного вращением треугольника BNC. Но треугольники равны между собой, а MD=a sin, поэтому и надо найти V, зная и . Поскольку , , то и . При , , получаем .

Решение 2-ой задачи:

Обозначим АВ=c, =. Тогда АС=c sin. ВС=c cos и объем тела, получающегося при вращении треугольника АВС вокруг прямой m, есть

V=ccossin.

Анологично объем тела, получающегося при вращении треугольника АВС вокруг прямой n, есть V=ccossin. Поскольку на рисунке, где проведены прямые АМ, ВN, перпендикулярные p, будет АМ=ВN=csincos, МС=csin и NC=ccos, то объем тела, получающегося при вращении треугольника АВС вокруг прямой p, есть

V=.

Отсюда , так что ()

И V=. При V= 65, V=156 получаем, чтоV =60.

Работа групп оценивается.

6. Подведение итогов урока и постановка домашнего задания.

Итак, задачи какого типа мы сегодня рассмотрели? ( задачи, в которых надо было найти объем комбинации тел вращения, причем эти тела не были даны изначально, а получались в процессе решения. Результаты вашей работы говорят, что вы справились с поставленной перед вами задачей.

Для домашнего задания вам предлагаются задачи 2-го типа, решения которых мы заслушаем и обсудим на следующем уроке:

В усеченный конус вписан шар, диаметр которого равен 5. Образующие конуса составляют с плоскостью основания угол в 60º.Найдите объем конуса.

В данный конус вписан другой конус, основание которого параллельно основанию данного конуса и делит его высоту в отношении 1:2, считая от вершины. Вершина вписанного конуса совпадает с центром основания данного. Найдите отношение объемов этих конусов.

Тест по теме «Тела вращения».

1)Какое из выражений является объемом тела вращения, получившегося при вращении прямоугольного треугольника, катеты которого 3см и 4см, вокруг большего катета?

1. 16 4. 12

2. 36 5. 15

3. нет правильного ответа

2)Прямоугольник со сторонами a и b(ab) вращаеться вокруг большей стороны. Найти объем полученного тела.

1. 2ba 4. a

2. 2ab 5. нет правильного ответа.

3.

3)Прямоугольная трапеция с основаниями 6см и 3см и образующей 5см вращается вокруг боковой стороны, перпендикулярной к основанию. Найти объем получившегося тела вращения.

1. 21 4. 66

2. 52 5. нет правильного ответа.

3. 84

4)В шар радиуса 2дм вписан конус, осевое сечение которого равносторонний треугольник. Найти объем конуса.

1. 3 4.

2. 24 5. 12

3. нет правильного ответа

5) Равнобедренный прямоугольный треугольник вращается вокруг гипотенузы равной 12см. Найти объем полученного тела вращения.

1. 36 4. 72

2. 144 5. нет правильного ответа.

3. 216

Тест по теме «Тела вращения».

1)Какое из выражений является объемом тела вращения, получившегося при вращении прямоугольного треугольника, катеты которого 3см и 4см, вокруг меньшего катета?

1. 12 4. 16

2. 15 5. 36

3. нет правильного ответа

2)Прямоугольник со сторонами a и b(ab) вращаеться вокруг меньшей стороны. Найти объем полученного тела.

1. a 4.

2. ab 5. нет правильного ответа.

3 2ba

3)Прямоугольная трапеция с основаниями 6см и 2см и образующей 5см вращается вокруг боковой стороны, перпендикулярной к основанию. Найти объем получившегося тела вращения.

1. 52 4. 64

2. 20 5. 106

3. нет правильного ответа.

4)В шар вписан конус, осевое сечение которого равносторонний треугольник с высотой 3см. Найти объем шара.

1. 288 4. 72

2. 5.

3.нет правильного ответа

5) Равнобедренный прямоугольный треугольник вращается вокруг гипотенузы равной 6см. Найти объем полученного тела вращения.

1. 9 4. 144

2. 18 5. нет правильного ответа.

3. 36

Задания для групп.

Объемы тел, получающихся при вращении ромба вокруг каждой из его диагоналей, равны, соответственно, 1 и . Найдите объем тела, получающегося при вращении ромба вокруг его стороны.

АВСD- равнобедренная трапеция с основаниями АD и ВС, в которую можно вписать окружность. Известно, что ВАD = , а объем тела, получающегося при вращении трапеции вокруг стороны ВС, равен 11. Найдите объем тела, получающегося при вращении трапеции вокруг стороны АD.

В усеченный конус вписан шар, диаметр которого равен 5. Образующие конуса составляют с плоскостью основания угол в 60º.Найдите объем конуса.

В данный конус вписан другой конус, основание которого параллельно основанию данного конуса и делит его высоту в отношении 1:2, считая от вершины. Вершина вписанного конуса совпадает с центром основания данного. Найдите отношение объемов этих конусов.

Урок по теме «Решение задач на вычисление объемов тел вращения»

проведен в 11 «б» классе МОУ лицей. Содержание урока соответствует программе по математике для классов с углубленным изучением математики. При планировании урока учтены психофизические особенности учащихся 11«б» класса и поставлены цели:

образовательная — сформировать умения решать задачи на вычисление объема комбинации тел вращения.

развивающая—развивать познавательный интерес учащихся в процессе решения задач повышенной сложности и умения преодолевать трудности при их решении.

воспитательная –воспитывать волю и настойчивость в достижении цели.

Для достижения поставленных целей в ходе урока использовался проблемно-деятельностный подход к обучению математике, так как содержание учебного материала усваивалось детьми в процессе выполнения ими деятельности, адекватной изучаемому материалу, на усвоение которого была направлена эта деятельность.

.В процессе урока осуществлялось :

— развитие логического мышления;

-развитие внимания, воображения, зрительной и слуховой памяти;

— развитие навыков самоконтроля;

-формирование навыков самостоятельной работы.

Считаю, что в ходе урока поставленные цели были достигнуты. Намеченный план и структура урока реализованы. Хронометраж соблюден. Учебный материал соответствует программе, знаниям, умениям и навыкам учащихся математического класса. Соблюдены гигиенические требования. Урок проведен в спокойной, доброжелательной обстановке. Наглядность, эстетичность способствовали более успешному усвоению учебного материала.

Итог урока подведен. Деятельность учащихся оценена. Домашнее задание задано. Считаю, что урок получился результативным.

Видео:Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

Прямоугольный треугольник с катетами 5 и 12 вращается вокруг гипотенузы?

Геометрия | 10 — 11 классы

Прямоугольный треугольник с катетами 5 и 12 вращается вокруг гипотенузы.

Найти объем тела вращения.

Объём получившейся при вращении фигуры равен сумме объёмов двух конусов с общим основанием, радиус которого равен высоте, проведенной из прямого угла исходного треугольника.

Гипотенуза АВ = √(AC² + BC²) = √(12² + 5²) = 13

Из площади прямоугольного треугольника высота, проведенная к гипотенузе, равна произведению катетов, деленному на гипотенузу.

Высота СО = СА•CB : AB

Площадь общего основания

Площади) — — — — — — Примечание : если запись некорректно отображается, обновите страницу.

Видео:Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

Найти высоту прямоугольного треугольника, проведённую к гипотенузе, если гипотенуза 10см, а один из катетов 5 )))?

Найти высоту прямоугольного треугольника, проведённую к гипотенузе, если гипотенуза 10см, а один из катетов 5 ))).

Видео:Вычисление площадей и объемов с помощью определённого интегралаСкачать

Катет прямоугольного треугольника 8, а его проекция на гипотенузу 4 см?

Катет прямоугольного треугольника 8, а его проекция на гипотенузу 4 см.

Видео:Запомни: все формулы для площади треугольникаСкачать

СРОЧНО?

1) Прямоугольная трапеция с большим основанием 8 см и боковыми сторонами 3 см и 5 см вращается вокруг большего основания.

Найдите объем тела вращения.

2) Прямоугольный треугольник с катетом а и прилежащим острым углом альфа вращается вокруг гипотенузы.

Найдите объем тела вращения.

Видео:Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Если взять прямоугольник и вращать его вокруг одной из сторон, то получится цилиндр?

Если взять прямоугольник и вращать его вокруг одной из сторон, то получится цилиндр.

А если взять прямоугольный треугольник, то при вращении получится конус.

Заполни таблицу фигурами, вращая которые можно получить изображенные тела.

Предложи свои фигуры и тела вращения.

Видео:Найдите объём фигуры, образованной вращением прямоугольного треугольникаСкачать

Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см?

Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см.

Найти второй катет и гипотенузу треугольника.

Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Дан Прямоугольный треугольник который вращается вокруг катетов, первый = 6 см, второй = 8?

Дан Прямоугольный треугольник который вращается вокруг катетов, первый = 6 см, второй = 8.

Видео:11 класс, 33 урок, Вычисление объемов тел с помощью определённого интегралаСкачать

Прямоугольная трапеция с основанием 5 см и боковыми сторонами 24 и 25 смвращается вокруг меньшего основания?

Прямоугольная трапеция с основанием 5 см и боковыми сторонами 24 и 25 см

вращается вокруг меньшего основания.

Найдите объем тела вращения.

Видео:Вычисление объемов тел вращения (применение определенного интеграла)Скачать

Как найти катет прямоугольного треугольника, если его гипотенуза равняется 27см, а проекция искаемого катета на гипотенузу — 3см?

Как найти катет прямоугольного треугольника, если его гипотенуза равняется 27см, а проекция искаемого катета на гипотенузу — 3см?

Видео:Построение натуральной величины треугольника методом вращенияСкачать

Помогите решить пожалуйста?

Помогите решить пожалуйста!

Прямоугольный треугольник вращается вокруг прямой, что содержит его гипотенузу.

Найдите объем тела вращения, если известны катет треугольника а и прилегающий к катету а угол [tex] beta [ / tex].

Видео:Объем тела вращения на примере тора. 2 способаСкачать

Прямоугольный треугольник кактет которого 3и 4 см вращающий вокруг оси совпадающий с гипотенузой ?

Прямоугольный треугольник кактет которого 3и 4 см вращающий вокруг оси совпадающий с гипотенузой .

Найти площадь поверхности фигуры вращения.

Видео:Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать

Найдите объем тела полученного вращением прямоугольного треугольника вокруг его большого катета, если площадь этого треугольника равна 12(см ^ 2), а один из катетов 6 см?

Найдите объем тела полученного вращением прямоугольного треугольника вокруг его большого катета, если площадь этого треугольника равна 12(см ^ 2), а один из катетов 6 см.

На этой странице сайта, в категории Геометрия размещен ответ на вопрос Прямоугольный треугольник с катетами 5 и 12 вращается вокруг гипотенузы?. По уровню сложности вопрос рассчитан на учащихся 10 — 11 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

🎦 Видео

11 класс, 30 урок, Объем прямоугольного параллелепипедаСкачать