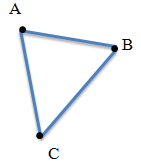
Треугольник — это геометрическая фигура, состоящая из трех точек, которые не лежат на одной прямой, и трех отрезков, последовательно соединяющих эти точки. Указанные точки называются вершинами треугольника, а отрезки — сторонами.
Данная фигура является треугольником (произносят: треугольник АВС, пишут: ∆ АВС). Точки А, В, С — вершины треугольника, а отрезки АВ, ВС, АС ‒ стороны.
Периметр треугольника — это сумма длин всех его сторон.
- Виды треугольников
- Математика. 5 класс
- Рисунки из треугольников
- Треугольник. Формулы и свойства треугольников.
- Типы треугольников
- По величине углов
- По числу равных сторон
- Вершины углы и стороны треугольника
- Свойства углов и сторон треугольника
- Теорема синусов
- Теорема косинусов
- Теорема о проекциях
- Формулы для вычисления длин сторон треугольника
- Медианы треугольника
- Свойства медиан треугольника:
- Формулы медиан треугольника
- Биссектрисы треугольника
- Свойства биссектрис треугольника:
- Формулы биссектрис треугольника
- Высоты треугольника
- Свойства высот треугольника
- Формулы высот треугольника
- Окружность вписанная в треугольник
- Свойства окружности вписанной в треугольник
- Формулы радиуса окружности вписанной в треугольник
- Окружность описанная вокруг треугольника
- Свойства окружности описанной вокруг треугольника
- Формулы радиуса окружности описанной вокруг треугольника
- Связь между вписанной и описанной окружностями треугольника
- Средняя линия треугольника
- Свойства средней линии треугольника
- Периметр треугольника
- Формулы площади треугольника
- Формула Герона
- Равенство треугольников
- Признаки равенства треугольников
- Первый признак равенства треугольников — по двум сторонам и углу между ними
- Второй признак равенства треугольников — по стороне и двум прилежащим углам
- Третий признак равенства треугольников — по трем сторонам
- Подобие треугольников
- Признаки подобия треугольников
- Первый признак подобия треугольников
- Второй признак подобия треугольников
- Третий признак подобия треугольников
- 📺 Видео
Видео:ТРЕУГОЛЬНИК и его виды. §14 математика 5 классСкачать

Виды треугольников
- Остроугольный треугольник — это треугольник, у которого всетри углаострые.
- Тупоугольный треугольник — это треугольник, у которого один из углов тупой.
- Прямоугольный треугольник — это треугольник, у которого один из углов прямой.
Сумма углов любого треугольника равна 180 0 .
По количеству равных сторон:
- Равнобедренный треугольник — это треугольник, у которого две стороны равны.
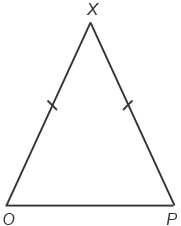
∆OXP — равнобедренный: XO = XP. Равные стороны на рисунке отмечают равным количеством чёрточек (в нашем случае одной чёрточкой). В равнобедренном треугольники равные стороны называют боковыми сторонами, а третью сторону — основанием, т.е. в ∆OXP: XO и XP — боковые стороны, а OP — основание.
- Равносторонний треугольник — это треугольник, у которого все стороны равны.
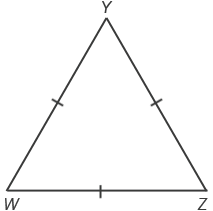
∆WYZ — равносторонний: WY = YZ = ZW. Равносторонний треугольник также называют правильным. Если сторона равностороннего треугольника равна 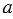
P = 3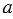 |
- Разносторонний треугольник — это треугольник, у которого все стороны имеют различную длину.
Поделись с друзьями в социальных сетях:
Видео:Математика 5 класс (Урок№28 - Треугольники.)Скачать

Математика. 5 класс
Конспект урока
Перечень рассматриваемых вопросов:
Треугольник – это геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой и соединённых между собой.
Периметр треугольника – сумма длин всех сторон треугольника.
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
1. Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Среди всех многоугольников наименьшее число сторон и углов имеет треугольник. Он является простейшей фигурой, и казалось бы, его изучение не может быть интересным. Однако существует множество видов треугольников. О них мы и поговорим.
Отметим какие-нибудь три точки, не лежащие на одной прямой – например, А, В, С. Соединим их с помощью линейки. Получим геометрическую фигуру, которая называется треугольником. Отмеченные три точки А, В, С называются вершинами, отрезки АВ, ВС, АС – сторонами треугольника, а углы А, В, С – углами треугольника.
Все треугольники можно разделить на группы по сторонам:
— если равных сторон нет – это разносторонний треугольник;
— если две стороны равны – это равнобедренный треугольник;
— если все стороны равны – это равносторонний треугольник.
Треугольники можно разделить на группы в зависимости от углов:
— если есть тупой угол – это тупоугольный треугольник;
— если все углы острые – это остроугольный треугольник;
— если есть прямой угол – это прямоугольный треугольник.
Треугольники, соединяясь друг с другом, могут образовывать другие фигуры.
Попробуем нарисовать прямоугольный треугольник на листе в клетку. Мы знаем, что сторона стандартной клетки – пять миллиметров, следовательно, две клетки – это один сантиметр.
По сторонам клетки проведём отрезки заданной длины из одной точки. В нашем случае из точки А проведём отрезки длиной четыре и три сантиметра, что соответствует восьми и шести клеткам. На концах отрезков поставим точки В и С и соединим их между собой. Таким образом, мы построили прямоугольный треугольник АВС.
А теперь рассмотрим свойства треугольников. Одно из них – жёсткость. Это свойство заключается в том, что, если взять три рейки и соединить их попарно, то получится треугольник, изменить форму которого можно лишь сломав рейку.
Рассмотрим ещё одно свойство треугольников. Оно заключается в том, что длина каждой стороны треугольника всегда меньше суммы двух других сторон.
Это свойство можно использовать для проверки возможности построения треугольника по определённым сторонам. То есть, если свойство не выполняется, то такого треугольника не может быть.
Если мы знаем стороны треугольника, то можем найти его периметр как сумму длин всех его сторон. Например, периметр треугольника АВС – это сумма сторон АВ, АС и ВС.
Измерим с помощью линейки стороны треугольника и рассчитаем его периметр.
По результатам измерения стороны, соответственно, равны пяти, шести и семи сантиметрам.
Значит, периметр равен восемнадцати сантиметрам, то есть сумме всех сторон.
Говоря о треугольниках, стоит упомянуть, что они бывают как одинаковыми, так и разными. Определить, равные или разные треугольники, можно способом наложения. Если треугольник полностью накладывается на другой треугольник, такие треугольники равны. В противном случае треугольники не будут равными.
Видео:Треугольник и его виды. 5 классСкачать

Рисунки из треугольников
Многие люди, как маленькие, так и взрослые, очень любят рисовать. Но иногда одного желания рисовать недостаточно. Для того чтобы облегчить процесс создания простейших картинок, инженер Эриф Мд. Вейлиула Байан, разработчик инновационного контента для детей, создал схемы, по которым, имея базовые навыки работы с чертёжными инструментами, можно создать милые и забавные картинки с животными и птицами.
Похожие схемы частично есть в открытом доступе, поэтому каждый желающий может приобщиться к миру изобразительного искусства через поэтапное прорисовывание простых картинок.
№ 1. В треугольнике все стороны равны 15 см. Чему равен периметр треугольника?
Решение: для нахождения периметра используем формулу Р = АВ + АС + ВС.
Так как у этого треугольника стороны равны, то Р = 15 см + 15 см + 15 см = 45 см
№ 2. Сопоставьте треугольники с их видами (по углам).
Решение: в задаче требуется сопоставить треугольники со следующими видами по углам: остроугольный, прямоугольный, тупоугольный. Согласно определению, прямоугольный треугольник имеет один угол 90 градусов: этому треугольнику соответствует второй треугольник. А тупоугольный треугольник имеет один угол больше 90 градусов: он отображён третьим по счёту. Как мы знаем, остроугольный треугольник имеет три угла меньше 90 градусов, так что в этом случае подходит треугольник, изображённый первым слева.
Видео:КАК ИЗМЕРИТЬ УГЛЫ ТРЕУГОЛЬНИКА ТРАНСПОРТИРОМ? Примеры | МАТЕМАТИКА 5 классСкачать

Треугольник. Формулы и свойства треугольников.
Видео:ЕГЭ 2024. ВСЁ ПРО ТРЕУГОЛЬНИКИ за 15 минутСкачать

Типы треугольников
По величине углов
По числу равных сторон
Видео:математика 5 класс Треугольник и его виды. Построение треугольниковСкачать

Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 — 2 bc · cos α
b 2 = a 2 + c 2 — 2 ac · cos β
c 2 = a 2 + b 2 — 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Видео:Виды треугольниковСкачать

Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 — a 2
mb = 1 2 √ 2 a 2 +2 c 2 — b 2
mc = 1 2 √ 2 a 2 +2 b 2 — c 2
Видео:Виды треугольниковСкачать

Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p — a ) b + c
lb = 2√ acp ( p — b ) a + c
lc = 2√ abp ( p — c ) a + b
где p = a + b + c 2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Видео:Математика 5 класс: Треугольник и его виды.Скачать

Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )
Видео:Сравнение углов. Виды углов. Чертежный треугольник. 5 класс.Скачать

Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Связь между вписанной и описанной окружностями треугольника
Видео:ТРЕУГОЛЬНИКИ И ИХ ВИДЫ. Видеоурок | МАТЕМАТИКА 5 классСкачать

Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Видео:КАК НАЙТИ ПЕРИМЕТР ТРЕУГОЛЬНИКА? Примеры | МАТЕМАТИКА 5 классСкачать

Формулы площади треугольника
Формула Герона
| S = | a · b · с |
| 4R |
Видео:МАТЕМАТИКА 5 класс: Отрезок | Длина отрезка | ТреугольникСкачать

Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k — коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
📺 Видео
ВСЯ математика 5-го класса в одном видео! Альфа-школаСкачать

Отрезок. Длина отрезка. Треугольник | Математика 5 класс #2 | ИнфоурокСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать