- Типы треугольников
- По величине углов
- По числу равных сторон
- Вершины углы и стороны треугольника
- Свойства углов и сторон треугольника
- Теорема синусов
- Теорема косинусов
- Теорема о проекциях
- Формулы для вычисления длин сторон треугольника
- Медианы треугольника
- Свойства медиан треугольника:
- Формулы медиан треугольника
- Биссектрисы треугольника
- Свойства биссектрис треугольника:
- Формулы биссектрис треугольника
- Высоты треугольника
- Свойства высот треугольника
- Формулы высот треугольника
- Окружность вписанная в треугольник
- Свойства окружности вписанной в треугольник
- Формулы радиуса окружности вписанной в треугольник
- Окружность описанная вокруг треугольника
- Свойства окружности описанной вокруг треугольника
- Формулы радиуса окружности описанной вокруг треугольника
- Связь между вписанной и описанной окружностями треугольника
- Средняя линия треугольника
- Свойства средней линии треугольника
- Периметр треугольника
- Формулы площади треугольника
- Формула Герона
- Равенство треугольников
- Признаки равенства треугольников
- Первый признак равенства треугольников — по двум сторонам и углу между ними
- Второй признак равенства треугольников — по стороне и двум прилежащим углам
- Третий признак равенства треугольников — по трем сторонам
- Подобие треугольников
- Признаки подобия треугольников
- Первый признак подобия треугольников
- Второй признак подобия треугольников
- Третий признак подобия треугольников
- Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов
- Формулы радиусов вписанной и описанной окружностей 9 класс
- Формулы радиусов вписанной и описанной окружностей. Построение некоторых правильных многоугольников. план-конспект урока по геометрии (9 класс) на тему
- Скачать:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- Презентации двух уроков по геометрии на тему «Формулы для радиусов вписанных и описанных окружностей правильных многоугольников» (9 класс)
- Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
- Выберите документ из архива для просмотра:
- Описание презентации по отдельным слайдам:
- Описание презентации по отдельным слайдам:
- Краткое описание документа:
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Формулы для радиусов вписанных и описанных окружностей правильных многоугольников.
- Просмотр содержимого документа «Формулы для радиусов вписанных и описанных окружностей правильных многоугольников.»
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Типы треугольников
По величине углов
По числу равных сторон
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 — 2 bc · cos α
b 2 = a 2 + c 2 — 2 ac · cos β
c 2 = a 2 + b 2 — 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 — a 2
mb = 1 2 √ 2 a 2 +2 c 2 — b 2
mc = 1 2 √ 2 a 2 +2 b 2 — c 2
Видео:Формулы для радиусов вписанной и описанной окружностей треугольника Геометрия 9классСкачать

Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p — a ) b + c
lb = 2√ acp ( p — b ) a + c
lc = 2√ abp ( p — c ) a + b
где p = a + b + c 2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Видео:Геометрия. 9 класс. Формулы для нахождения радиусов вписанной и описанной окружностей треугольникаСкачать

Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )
Видео:Формула радиуса описанной окружности треугольника. Геометрия 9 классСкачать

Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Связь между вписанной и описанной окружностями треугольника
Видео:Геометрия 9 класс. Вписанные и описанные окружности. Ключевая задача № 4.Скачать

Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Видео:Формула радиуса вписанной окружности треугольника. Геометрия 9 классСкачать

Формулы площади треугольника
Формула Герона
| S = | a · b · с |
| 4R |
Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k — коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов
Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.
Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.
Вокруг любого треугольника можно описать окружность, причем только одну.
Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.
В любой треугольник можно вписать окружность, причем только одну.
Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник.
Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?
В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.
Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов.
Вот еще две формулы для площади.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.
— радиус окружности, вписанной в треугольник.
Есть и еще одна формула, применяемая в основном в задачах части :
где — стороны треугольника, — радиус описанной окружности.
Для любого треугольника верна теорема синусов:
Ты нашел то, что искал? Поделись с друзьями!
. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .
Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .
Запишем площадь треугольника АВС двумя способами:
Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .
В ответ запишем .
. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.
По теореме синусов,
Получаем, что . Угол — тупой. Значит, он равен .
. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.
Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.
, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем . Тогда .
Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .
Видео:С. р. #3. Вариант 2. 9 класс. Геометрия. Вписанные и описанные окружностиСкачать
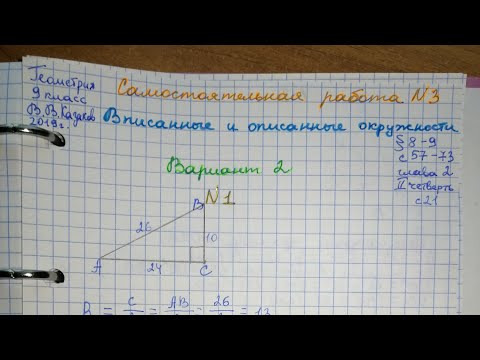
Формулы радиусов вписанной и описанной окружностей 9 класс
Видео:Тема 7. Вписанные и описанные окружности треугольникаСкачать

Формулы радиусов вписанной и описанной окружностей. Построение некоторых правильных многоугольников.
план-конспект урока по геометрии (9 класс) на тему
Конспект урока по теме «Формулы радиусов вписанной и описанной окружностей. Построение некоторых правильных многоугольников«
Видео:Запомни: все формулы для площади треугольникаСкачать

Скачать:
| Вложение | Размер |
|---|---|
| konspekt_po_geom.doc | 54 КБ |
Видео:Вписанные и описанные окружности. Геометрия 9 класс. Ключевая задача № 3.Скачать

Предварительный просмотр:
Тема: «Формулы радиусов вписанной и описанной окружностей. Построение некоторых правильных многоугольников».
Тема: «Формулы радиусов вписанной и описанной окружностей. Построение некоторых правильных многоугольников».
- Познакомить учащихся с формулами нахождения радиусов вписанной и описанной окружности.
- Научить построению некоторых правильных многоугольников с помощью циркуля и линейки.
- Продолжать развивать интерес к математике.
Тип урока: изучение нового материала.
Программно – дидактическое обеспечение : циркуль, линейка, разноцветные мелки.
- Оргмомент.
- Объяснение нового материала.
- Закрепление изученного материала.
- Итог урока.
Постановка целей и этапов урока, проверка отсутствующих.
- Объяснение нового материала (20 мин).
1. Формулы радиусов вписанной и описанной окружностей.
Заготавливается таблица на доске.
Выражение радиусов вписанной r и описанной R окружностей через сторону а.
R = a / (2sin (180º/n))
2. Построение некоторых правильных многоугольников.
Рассмотрим способы построения некоторых правильных многоугольников с помощью циркуля и линейки. Учащиеся справа строят чертёж, а слева записывают описание построения.
- Строим окружность.
- Выбираем произвольную точку А 1.
- Из точки А 1 радиусом окружности делаем засечки.
- Соединяем попарно полученные точки и получаем правильный шестиугольник.
- Построение аналогичное шестиугольнику.
2. Но из полученных шести точек на окружности, соединять надо через одну и получаем правильный треугольник.
3. Квадрат. 1. Строим окружность.
2. Проводим через центр окружности два перпендикулярных диаметра.
3. Соединяем полученные точки на окружности и получаем квадрат.
4. Построение из n – угольников 2n – угольников.
- Строим окружность.
- Строим квадрат.
- К сторонам квадрата проводим диаметрами серединные перпендикуляры.
- Полученные точки пересечения окружности и серединных перпендикуляров и вершины квадрата соединяем попарно.
- Получаем восьмиугольник.
Применяются правильные многоугольники при составлении пакетов.
3. Закрепление изученного материала (10мин).
- В окружность радиуса R = 12 см вписан правильный n – угольник. Определите его сторону и периметр, если:
А) n = 3; Б) n = 4; B) n = 6;
А) R = a / √3; 12 = a / √3 => a = 12√3
Б) R = a / √2; 12 = a / √2 => a = 12√2
B) R = a; a = 12; P = 6*12 = 72;
2. Около окружности радиуса r = 6 описан правильный n – угольник. Определите его сторону и периметр, если:
А) n = 3; Б) n = 4; B) n = 6;
А) r = a / 2√3; 6 = a / 2√3 => a = 12√3
Б) r = a / 2; 6 = a / 2 => a = 12
B) r = a√3 / 2; 6 = a√3 / 2 => a = 12 / √3 = 12√3 / 3 = 4√3
3. Для правильного n – угольника со сторонами а = 6 см найдите радиус R и r, если:
А) n = 3; Б) n = 4; B) n = 6;
А) R = a / √3 => R = 6 / √3 = 6√3 / 3 = 2√3 см;
r = a / 2√3 => r = 6 / 2√3 = 3√3 / 3 = √3 см.
Б) R = a / √2; => R = 6 / √2 = 6√2 / 2 = 3√2 см;
r = a / 2 => r = 6 / 2 = 3 см.
B) R = a => R = 6 см;
r = a√3 / 2 => r = 6√3 / 2 = 3√3 см.
4. Итог урока (2 мин).
Оценить работу класса на уроке и назвать учащихся, отличившихся на уроке.
П. 115, 116, 117. Нарисовать эскиз паркета на альбомном листе, состоящий из правильных фигур, но допускается один многоугольник неправильный.
Видео:Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

По теме: методические разработки, презентации и конспекты
Урок геометрии в 8 классе по теме «Вписанная и описанная окружность»
Презентация к уроку включает определения основных понятий, создание проблемной ситуации, а также развитие творческих способностей учащихся.
Рабочая программа по элективному курсу по геометрии «Решение планиметрических задач на вписанные и описанные окружности» 9 класс
Статистические данные анализа результатов проведения ЕГЭ говорят о том, что наименьший процент верных ответов традиционно дается учащимися на геометрические задачи. Задачи по планиметрии, включаемые в.
Урок геометрии в 9 классе по теме: «Формула для радиусов вписанной и описанной окружностей»
Презентация к уроку геометрии в 9 классе по теме: «Формула для радиусов вписанной и описанной окружностей».
Правильные многоугольники. Формулы радиусов вписанной и описанной окружностей.
Урок объяснения нового материала. Вывод формул радиусов вписанной и описанной окружностей. Заполнение таблицы.
Тест по теме «Правильный многоугольник. Вписанная и описанная окружности. Формулы площади правильного многоугольника , стороны правильного многоугольника и радиуса вписанной окружности в правильный многоугольник»
Тест по теме «Правильный многоугольник. Вписанная и описанная окружности. Формулы площади правильного многоугольника , стороны правильного многоугольника и радиуса вписанной окр.
Презентация «Правильный многоугольник.Вписанная и описанная окружности»
Презентация к уроку «Правильный многоугольник.Вписанная и описанная окружности".
Краткосрочный план урока геометрии для 9 класса по теме «Решение треугольников (вычисление площади треугольника через радиус вписанной или описанной окружности)».
В работе представлен краткосрочный план урока геометрии в 9 классе по теме «Решение треугольников». В ходе урока выполняются задания на развитие функциональной грамотности обучающихс.
Видео:Радиус описанной окружностиСкачать

Презентации двух уроков по геометрии на тему «Формулы для радиусов вписанных и описанных окружностей правильных многоугольников» (9 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику
Выберите документ из архива для просмотра:
Выбранный для просмотра документ Г-9, урок № 31.pptx
Описание презентации по отдельным слайдам:
Г-9, урок № 31 Составила учитель математики Гринюк Любовь Викторовна МАОУ Ильинская СОШ г. Домодедово Московской области Формулы для радиусов вписанных и описанных окружностей правильных многоугольников
Проверка домашнего задания
Настройся на урок Какой многоугольник называется правильным? Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
Настройся на урок По какой формуле вычисляется сумма углов правильного n-угольника?
Настройся на урок Как найти угол правильного n-угольника?
Классная работа Формулы для радиусов вписанных и описанных окружностей правильных многоугольников
Сегодня на уроке Выведем формулы, связывающие радиус описанной и радиус вписанной окружности со стороной а правильного п-угольника для п = 3, п = 4, п = 6 и научимся применять их к решению задач.
Изучение нового материала Вписанная и описанная окружность Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются этой окружности. Окружность называется описанной около многоугольника, если все его вершины лежат на этой окружности.
Изучение нового материала Вписанная и описанная окружность Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах.
Свойства правильного многоугольника Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник.
Формулы для вычисления Площадь правильного многоугольника Сторона правильного многоугольника Радиус вписанной окружности
Решите задачи № 1 Дано: R, n=3 Найти: а № 2 Дано: R, n=4 Найти: а № 3 Дано: R, n=6 Найти: а № 4 Дано: r, n=3 Найти: а № 5 Дано: r, n=4 Найти: а № 6 Дано: r, n=6 Найти: а К доске вызвать 6 учащихся для решения задач, с последующей проверкой.
Формулы для вычисления
Проверь свои знания 1. Найдите радиус окружности, вписанной в правильный треугольник, если сторона треугольника равна 5 см. Решение: 2. Радиус окружности, вписанной в квадрат, равен 1 см. Найдите радиус описанной окружности. Решение: 3. Радиус окружности, описанной около правильного шестиугольника, равен 7 см. Найдите сторону правильного шестиугольника. Решение:
Домашнее задание П.116, с. 172-173 № 21 № 24
Выбранный для просмотра документ Г-9, урок № 32.pptx
Описание презентации по отдельным слайдам:
Г-9, урок № 32 Составила учитель математики Гринюк Любовь Викторовна МАОУ Ильинская СОШ г. Домодедово Московской области Формулы для радиусов вписанных и описанных окружностей правильных многоугольников
Проверка домашнего задания
Настройся на урок Какой многоугольник называется правильным? Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
Настройся на урок По какой формуле вычисляется радиус описанной окружности правильного треугольника? Выразите сторону треугольника
Настройся на урок По какой формуле вычисляется радиус вписанной окружности правильного треугольника? Выразите сторону треугольника
Настройся на урок По какой формуле вычисляется радиус описанной окружности правильного четырехугольника? Выразите сторону квадрата
Настройся на урок По какой формуле вычисляется радиус вписанной окружности правильного четырехугольника? Выразите сторону квадрата
Настройся на урок По какой формуле вычисляется радиус описанной окружности правильного шестиугольника? Выразите сторону шестиугольника
Настройся на урок По какой формуле вычисляется радиус вписанной окружности правильного шестиугольника? Выразите сторону шестиугольника
Классная работа Формулы для радиусов вписанных и описанных окружностей правильных многоугольников
Сегодня на уроке Отработка применения формул, связывающих радиус описанной и радиус вписанной окружностей со стороной а правильного п-угольника для п = 3, п = 4, п = 6 к решению задач.
Решите задачи 1. В окружность радиуса R = 12 вписан правильный п-угольник. Определите его сторону и периметр, если п = 3, п = 4, п = 6. 2. Около окружности радиуса r = 6 описан правильный п-угольник. Определите его сторону и периметр, если п = 3, п = 4, п = 6. 3. Для правильного п-угольника со стороной а = 6 см найдите радиус описанной около него окружности, если п = 3, п = 4, п = 6.
Решите задачу Дано: S=16, n=4 Найти: a, r, R, P Мы знаем формулы: № 4 Найдите неизвестные величины.
Решите задачу № 5 Дано: P=6, n=3 Найти: R, a, r, S Мы знаем формулы: Найдите неизвестные величины.
Решите задачу № 6 Дано: Найти: Решение:
Домашнее задание П.116, с. 172-173 № 20 № 23
Проверь свои знания 2) Внешний угол правильного n-угольника равен 50º. Найдите его внутренний угол. 1) По какой формуле вычисляется сумма углов правильного n-угольника?
Проверь свои знания 3) Как найти угол правильного n-угольника? 4) Внутренний угол правильного n-угольника равен 150º. Найдите его внешний угол. Самостоятельная работа
Выбранный для просмотра документ Самостоятельная.docx
№ 1. Сколько сторон имеет правильный п- угольник, если его внешний угол равен 20º?
№ 2. Правильный треугольник вписан в окружность радиуса 5 см. Определите радиус окружности, вписанной в этот треугольник.
№ 1. Сколько сторон имеет правильный п- угольник, если его внутренний угол равен 140º?
№ 2. Правильный шестиугольник вписан в окружность радиуса 4 см. Определите радиус окружности, вписанной в этот шестиугольник.
Краткое описание документа:
Данный материал состоит из двух уроков-презентаций по данной теме.
Урок первый – изучение нового материала, на котором вводятся формулы, связывающие радиусы вписанной и описанной окружностей для правильных п-угольников со стороной а при п = 3, п = 4, п = 6; формируются умения применять полученные знания при решении простейших задач.
Урок второй – закрепление полученных знаний, на котором вначале проверяется ранее изученный материал о правильных многоугольниках вписанных в окружность и описанных около окружности, проверяется знание формул из предыдущего урока на устных заданиях. Второй этап урока – это решение стандартных задач. Третий этап – проверка знаний по применению формул, связывающих радиусы вписанной и описанной окружностей для правильных п-угольников со стороной а при п = 3, п = 4, п = 6.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 942 человека из 79 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 678 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 305 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 520 372 материала в базе
Другие материалы
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 11.12.2014 23619
- ZIP 1.4 мбайт
- 1228 скачиваний
- Рейтинг: 4 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Гринюк Любовь Викторовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 7 лет и 1 месяц
- Подписчики: 0
- Всего просмотров: 85255
- Всего материалов: 10
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Путин поручил обучать педагогов работе с девиантным поведением
Время чтения: 1 минута
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
Большинство российских вузов используют смешанный формат обучения
Время чтения: 1 минута
Школы Пскова перевели на дистанционное обучение
Время чтения: 2 минуты
В Госдуме предложили создать в школах «ящики доверия» для обращений к психологу
Время чтения: 1 минута
Минобрнауки учредит стипендию для студентов — победителей международных олимпиад
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Формулы для радиусов вписанных и описанных окружностей правильных многоугольников.
Презентация урока геометрии 9 класса по теме «Формулы для радиусов вписанных и описанных окружностей правильных многоугольников».
Просмотр содержимого документа
«Формулы для радиусов вписанных и описанных окружностей правильных многоугольников.»
Формулы для радиусов
вписанных и описанных окружностей правильных многоугольников.
Выполнил: учитель математики Аюбов Р.К.
Актуализация опорных знаний
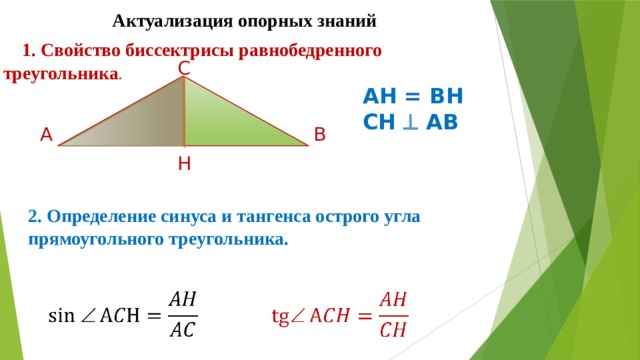
1. Свойство биссектрисы равнобедренного треугольника .
2. Определение синуса и тангенса острого угла прямоугольного треугольника.
Цели: ввести формулы, связывающие радиусы R описанной и r вписанной окружностей для правильного многоугольника со стороной а и числом сторон п ; формировать умение применять полученные знания при решении задач; повышение уровня мотивации учащихся к изучению геометрии.
Высшее проявление духа – это разум.
Высшее проявление разума – это геометрия.
Клетка геометрии – треугольник.
Он так же неисчерпаем, как и вселенная.
Окружность – душа геометрии.
Познайте окружность, и вы не только познаете
Душу геометрии, но и возвысите свою душу.
1. Найдите угол правильного пятиугольника, шестиугольника, восьмиугольника.
2. Найдите количество сторон правильного многоугольника, если его внутренний угол равен 108 градусам.
1. Найдите угол правильного восьмиугольника.
2. Найдите количество сторон правильного многоугольника, если его внутренний угол равен 108 градусам.
Вокруг всякого правильного n-угольника можно описать окружность. Центр окружности – точка пересечения серединных перпендикуляров сторон многоугольника.
В каждый правильный многоугольник можно описать окружность. Центр окружности – точка пересечения биссектрис углов.
Вписанная и описанная окружности правильного многоугольника имеют общий центр. Он называется центром данного правильного многоугольника.
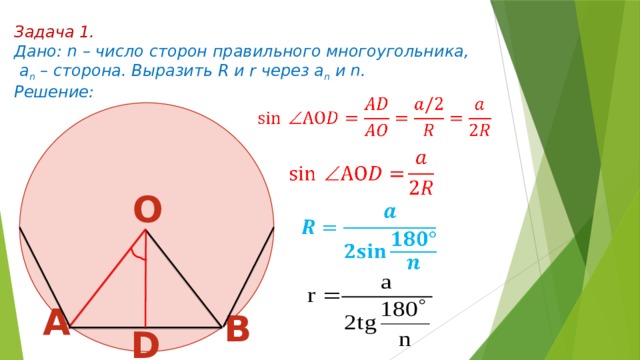
Дано: n – число сторон правильного многоугольника,
a n – сторона. Выразить R и r через а n и n.
Выразить сторону правильного шестиугольника через R и r.
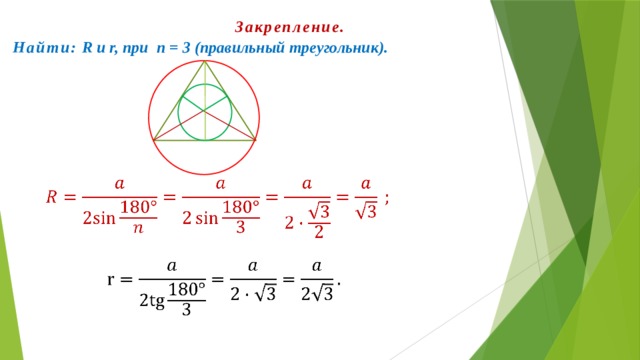
Найти: R и r, при n = 3 (правильный треугольник).
Найдите площадь квадрата, описанного около окружности радиуса 16.
Площадь круга 69. Найдите площадь сектора этого
круга, центральный угол которого равен 120 .
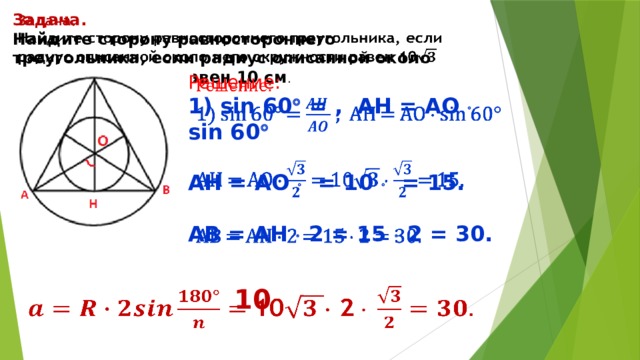
Найдите сторону равностороннего треугольника, если радиус описанной около него окружности равен 10 см .
Найдите площадь квадрата, описанного около круга площадью 25 .
– У какого выпуклого многоугольника все внешние углы прямые?
– Приведите пример такого выпуклого многоугольника, у которых все стороны равны, но он не является правильным.
Домашнее задание: подготовить тематическую таблицу «Правильный многоугольник»; № 22; № 17 (В7).