Все формулы правильных треугольников

В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.

Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Определение равностороннего треугольника

Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.

Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Свойства равностороннего треугольника

Свойство 1

В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.

Свойство 2

В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.

CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.

Свойство 3

В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.

Свойство 4

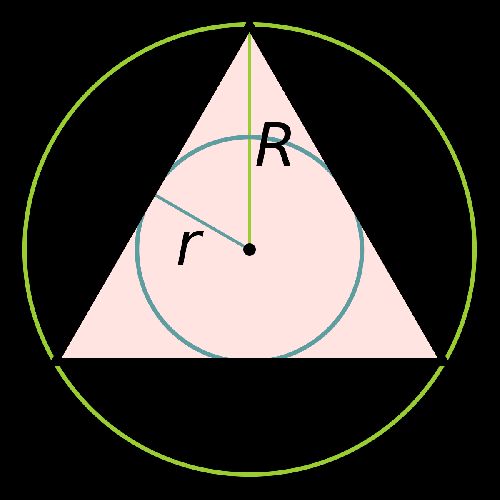
Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.

Свойство 5

Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.

• R – радиус описанной окружности;
• r – радиус вписанной окружности;
• R = 2r.

Свойство 6

В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:

1. Высоту/медиану/биссектрису:

2. Радиус вписанной окружности:

3. Радиус описанной окружности:

4. Периметр:

5. Площадь:

Видео:Формулы равностороннего треугольника #shortsСкачать

Пример задачи

Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.

Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:

Видео:Формулы для равностороннего треугольника.Скачать

Правильный треугольник

Средняя оценка: 4.6

Всего получено оценок: 80.

Средняя оценка: 4.6

Всего получено оценок: 80.

Правильный треугольник имеет много специфических свойств, которые значительно упрощают решение задач. Поэтому имеет смысл поговорить о каждом из этих свойств, дабы облегчить решение задач.

Видео:Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать

Определение

Правильный треугольник – это треугольник, у которого все стороны равны и каждый угол равен 60 градусам. Правильный треугольник еще называют равносторонним. О формулах правильного треугольника, и о том, как производить по ним различные вычисления – поговорим ниже.

Рис. 1. Правильный треугольник.

Видео:ЕГЭ 2024. ВСЁ ПРО ТРЕУГОЛЬНИКИ за 15 минутСкачать

Формулы правильного треугольника

Почти все формулы вытекают из утверждения о том, что правильный треугольник имеет 3 угла по 60 градусов и 3 одинаковые стороны.

Площадь

Начнем с формулы площади.

Равносторонний треугольник любой высотой делится на два, равных между собой прямоугольных треугольника. Теперь найдем значение высоты, подставим его в классическую формулу площади треугольника и получим формулу для нахождения площади правильного треугольника.

Рис. 2. Рисунок к доказательству.

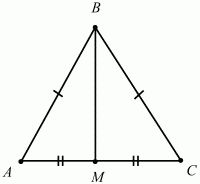
В прямоугольном треугольнике АВМ катет ВМ можно выразить через синус угла ВАМ. Этот угол известен и равен 60 градусам, значит, известны и значения синуса и косинуса для этого угла. Катет ВМ противолежащий, значит, для его нахождения необходимо воспользоваться формулой синуса.

С другой стороны синус 60 градусов заранее известнее и равен $sqrt over 2$ . Значит можно выразить значение АМ:

Все стороны треугольника между собой равны, поэтому для удобства обозначим их через букву а.

Тогда формула будет выглядеть следующим образом:

Теперь вспомним классическую формулу площади треугольника:

$S= h*a$, где а это основание треугольника, h – высота, проведенная к этому основанию. В заданном треугольнике это будет выглядеть следующим образом:

Получившаяся формула гораздо проще классических в плане количества необходимых параметров. Для нахождения площади правильного треугольника необходимо знать только значение одной из его сторон. Это возможно за счет равенства углов в таком треугольнике.

Только в правильном треугольнике возможно нахождение площади через значение одной стороны.

Периметр

Периметр найти ещё проще, так как это сумма всех сторон треугольника, а они все равны между собой, то:

Подобный подход, где приравниваются стороны или используются свойства медиан и биссектрис равностороннего треугольника, часто используется при решении подобных задач. У правильного треугольника нет и не может объема, так как это плоская фигура. У нее два характеризующих понятия: площадь и периметр.

В равностороннем треугольнике каждая биссектриса совпадает с медианой и высотой. Также совпадают и точки пересечения этих отрезков. Получившаяся точка зовется центром фигуры.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Что мы узнали?

Из статьи мы узнали, что у правильного треугольника все стороны и углы равны между собой. Мы узнали о свойствах биссектрисы, медианы и высоты – в правильном треугольнике это будет одна и та же линия. Ее можно проводить от любой вершины.

Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Правильный треугольник. Площадь правильного треугольника

Правильный треугольник — треугольник, у которого все стороны равны. Каждый угол правильного треугольника равен градусов.
Правильный треугольник называют еще равносторонним.

Каждая из высот правильного треугольника является также его медианой и биссектрисой.
Центры вписанной и описанной окружностей правильного треугольника совпадают.

Пусть сторона правильного треугольника равна .

Высота правильного треугольника:
Радиус окружности, вписанной в правильный треугольник: .
Радиус описанной окружности в два раза больше: .
Площадь правильного треугольника: .

Все эти формулы легко доказать. Если вы нацелены на решение задач части — докажите их самостоятельно.

. Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.

Задача решается в одну строчку. Радиус вписанной окружности .

. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна .

Сравним формулы для высоты правильного треугольника и радиуса вписанной окружности. Очевидно, радиус вписанной окружности равен высоты.

. Сторона правильного треугольника равна . Найдите радиус окружности, описанной около этого треугольника.

Радиус окружности, описанной вокруг правильного треугольника, равен .

📹 Видео

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Геометрия - Построение правильного треугольникаСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Всё про прямоугольный треугольник за 15 минут | Осторожно, спойлер! | Борис Трушин !Скачать

Все формулы по геометрии для ЕГЭСкачать

Площадь треугольника. Как найти площадь треугольника?Скачать

11 класс, 47 урок, Формулы площади треугольникаСкачать

112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписаннойСкачать

Правильные треугольник, четырехугольник и шестиугольник (вывод основных формул)Скачать

👉 ФОРМУЛА ГЕРОНА. Площадь треугольника #shortsСкачать

Math | triangle | hexagon | Формулы правильных треугольника и шестиугольникаСкачать