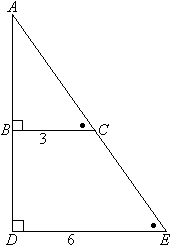Все формулы подобных треугольников (4 видео)

Подобные треугольники

Содержание

Определение
Признаки подобия треугольников
Свойства подобных треугольников
Примеры наиболее часто встречающихся подобных треугольников
Подобные треугольники — признаки, свойства и теоремы
Общие сведения
Объекты геометрии
Основные аксиомы Евклида
Подобие двух треугольников
Первое условие
Второй критерий
Третий признак
Теорема об отношении площадей
Некоторые свойства и следствия
Пример решения
Подобные треугольники
Определение
Практические задачи с подобными треугольниками
Практические примеры
🎥 Видео

Видео:Подобные треугольникиСкачать

Определение

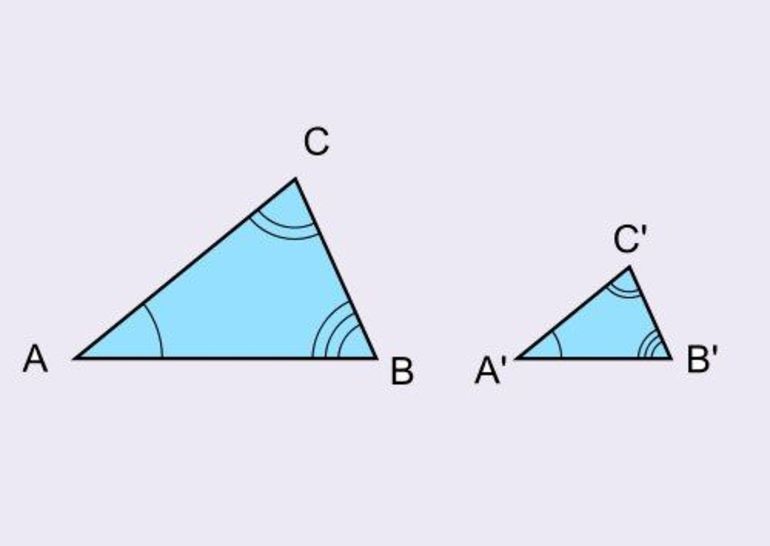
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

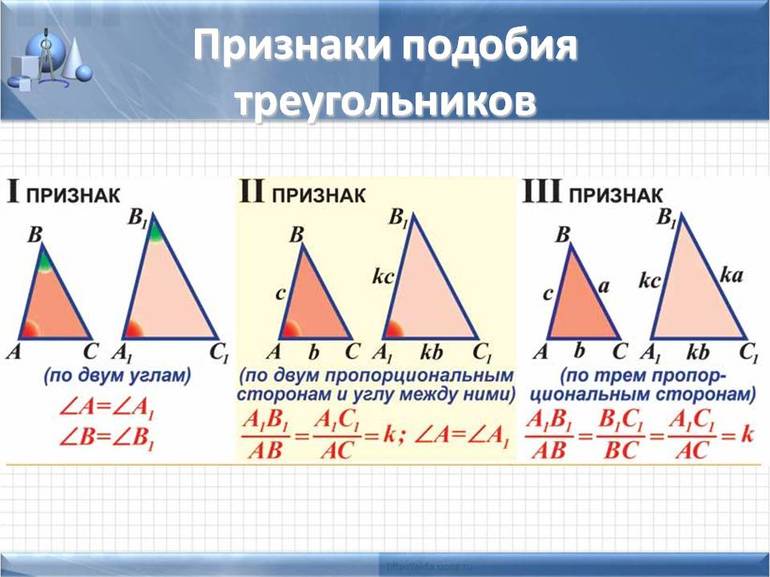
Признаки подобия треугольников

I признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Свойства подобных треугольников

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Отношение периметров подобных треугольников равно коэффициенту подобия.
Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.

Видео:ПОДОБНЫЕ ТРЕУГОЛЬНИКИ коэффициент подобия 8 классСкачать

Примеры наиболее часто встречающихся подобных треугольников

1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

Здесь вы найдете подборку задач по теме «Подобные треугольники» .

Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Подобные треугольники — признаки, свойства и теоремы

Видео:Решение задач на тему "Подобные треугольники". 8 классСкачать

Общие сведения

Специалисты рекомендуют начинать любое обучение с азов. Следует применять принцип, который называется «от простого к сложному». В плоскостной геометрии (Евклида) существует два понятия: аксиомы и теоремы. К первым относятся утверждения, не требующие доказательства. Они являются базовыми элементами науки и позволяют доказывать другие гипотезы или утверждения.

Кроме того, на основании доказанных гипотез можно производить операции по доказательству более сложных теорем. Иными словами, геометрия состоит из базисных элементов — аксиом, при использовании которых можно преобразовывать утверждения в неоспоримые факты, а также при комбинациях появляется возможность доказательства более сложных (составных) элементов. Примером последнего случая является гипотеза Пифагора для прямоугольного треугольника. Чтобы ее доказать, нужно знать аксиомы геометрии, а также теорему об отношении площадей подобных треугольников (S/S’). Далее необходимо разобрать основные объекты геометрии.

Объекты геометрии

Простейшим объектом геометрии является точка. С помощью нее строятся простые фигуры, благодаря которым образуются более сложные формы. К элементарным компонентам можно отнести следующие: прямая, отрезок, луч. Первая состоит из множества точек, соединенных между собой в одной плоскости и находящихся в поперечном сечении, диаметр которого эквивалентен диаметру точек. При соединении простейших объектов получается бесконечная линия без перегибов.

Лучом называется часть прямой, имеющая начальную точку, но у которой нет конечной границы. Еще существует один элемент, у которого присутствуют обе границы (левая и правая). Он называется отрезком. Следует отметить, что луч и отрезок могут лежать на одной прямой, а также последний может являться частью первого.

При комбинации двух лучей, исходящих из одной точки получается плоский угол. Он измеряется в градусах или радианах. Следует отметить, что в геометрии существует понятие «нулевого» угла. Это возможно, когда лучи совпадают. При комбинации трех углов можно получить треугольник. Существует также другое определение этой фигуры: треугольником (Δ) называется фигура, состоящая из трех точек, одна из которых не лежит на одной прямой с остальными.

Треугольники бывают разносторонними, равнобедренными и равносторонними. Кроме того, в зависимости от градусной меры, они делятся на такие классы: остроугольные, тупоугольные и прямоугольные. Необходимо также отметить, что сумма углов этой геометрической фигуры эквивалентна 180 градусам.

Нужно обратить внимание на такие термины: высоту, медиану и биссектрису. Первой называется перпендикуляр, проведенный из вершины к противоположной стороне. Медиана — отрезок, проведенный из противоположной вершины к середине стороны. Биссектрисой угла является луч или отрезок, который делит его на два равнозначных по величине. В равнобедренном и равностороннем Δ эти элементы совпадают.

Основные аксиомы Евклида

Аксиомой называется утверждение, не требующее доказательств и воспринимаемое в виде факта. Существуют следующие утверждения, которые можно применять при решении задач:

Если на плоскости существует некоторая прямая, то в этом случае точки классифицируются на две группы по отношению к ней: лежащие и не лежащие.
Через две точки можно провести только одну прямую.
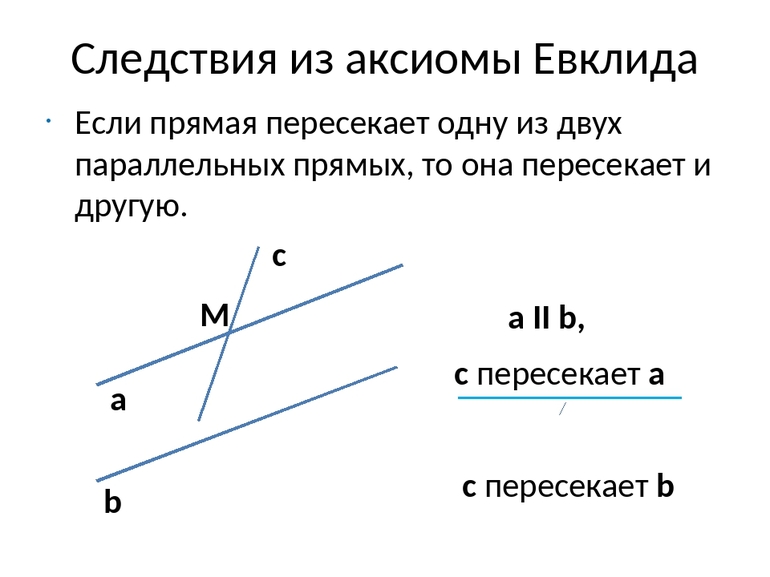
При заданных прямой и точке, не лежащей на ней, через последнюю можно провести только одну прямую, которая будет параллельна (||) исходной.
Когда даны три угла, один из которых эквивалентен другому, а последний — третьему, тогда можно сделать вывод об их равенстве. Аналогичное утверждение существует и для отрезков.
Любая прямая содержит две точки, а также точку, лежащую между ними.
Точки, находящиеся на одной плоскости, могут соединяться в любой последовательности вспомогательными отрезками.

Следует обратить внимание на последнюю аксиому. Она позволяет строить любые фигуры на плоскости и в пространстве. Математики очень часто применяют такой прием при решении задач и доказательстве некоторых тождеств при помощи создания дополнительных элементов на чертеже.

Например, в некотором упражнении по нахождению отдельных параметров треугольника в условии содержится очень мало данных. Последний можно вписать в окружность или дополнить до квадрата или прямоугольника. Далее следует разобраться в признаках подобия треугольников.

Видео:Подобные треугольники с нуля до ОГЭ | Математика ОГЭ 2023 | УмскулСкачать

Подобие двух треугольников

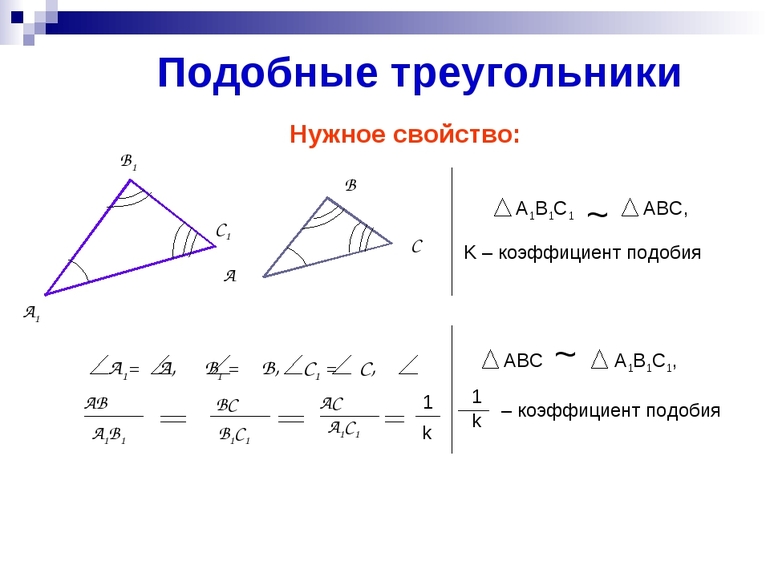
Треугольники являются подобными, когда углы одного эквивалентны всем градусным мерам углов другого, а стороны одного равны сторонам другого, с учетом коэффициента гомотетии. Последний называют еще коэффициентом подобия. Он равен отношению сторон подобных треугольников. Например, дано два подобных Δ ABC и A’B’C’ (больший). Коэффициент подобия треугольников обозначается литерой «k». Он больше 0 и вычисляется по такой формуле: k = A’B’ / AB = B’C’ / BC = A’C’ / AC. Подобие фигур обозначается таким образом: ΔABC ∼ ΔA’B’C’.

Не во всех случаях бывают известны углы и стороны фигур. Для этого были сформулированы три признака (условия или критерия), по которым можно определить подобие.

Первое условие

Формулировка первого признака подобия треугольников гласит, что равенство двух углов между собой соответствует подобию двух фигур. Подробнее исходные данные записываются в таком виде: ΔABC ∼ ΔA’B’C’, когда ∠ВАС = ∠B’A’C’ и ∠ABC = ∠A’B’C’. Доказать утверждение довольно просто. Для этого следует рассчитать третий угол у треугольников исходя из того, что сумма трех углов составляет 180 градусов.

Далее необходимо наложить один Δ на другой, чтобы ∠ВАС совпал с ∠B’A’C’. Используя теорему Фалеса для сторон угла, которые делят на отрезки AC / A’C’ = BC / B’C’ вершины малого Δ на пропорциональные части. Аналогично доказывается пропорциональность для двух других сторон. Однако для этого следует наложить уже треугольники таким образом, чтобы совпали другие углы. Такие же действия проделать и для третьего угла. На основании определения о подобии треугольников утверждение доказано. Из доказательства математики получили некоторые следствия, которые будут очень полезны при решении задач:

Фигуры (Δ) подобны при параллельности 3 сторон одного Δ сторонам другого, при перпендикулярности одно стороны другой, а также отсутствия || двух сторон одного Δ сторонам другого.
Фигура, полученная при помощи параллельного переноса со сторонами, которые умножаются на некоторый постоянный коэффициент, подобна исходной.

Равенство AC / A’C’ = BC / B’C’ эквивалентно коэффициенту подобия. Этот факт можно использовать при решении задач и доказательства других геометрических утверждений или тождеств.

Второй критерий

Математики выделяют еще один признак подобия треугольников по двум пропорциональным сторонам и углу между ними. Для доказательства следует рассмотреть ΔABC и ΔA’B’C’ со сторонами, связанными таким тождеством: AB / A’B’ = AC / A’C’. Кроме того, углы между ними равны: ∠ВАС = ∠B’A’C’. Далее нужно достроить ΔABC до четырехугольника ABCС». Вершина С» должна располагаться в зеркальном отображении относительно стороны AB. Полученный ΔABC» ∼ ΔA’B’C’ по I признаку, поскольку у них два угла равны. Следовательно, тождество можно править таким образом: AB / A’B’ = AC» / A’C’.

По условию должно выполняться условие AB / A’B’ = AC / A’C’. Тогда AC = AC». На основании этого факта можно сделать вывод о равенстве ΔABC и ΔABC». Следовательно, теорема доказана, поскольку эти треугольники (ΔABC» и ΔA’B’C’) подобны по I признаку.

Третий признак

Третий признак подобия двух треугольников формулируется таким образом: два треугольника являются подобными, когда стороны одного пропорциональны сторонам другой фигуры. Для доказательства необходимо рассмотреть ΔABC и ΔA’B’C’ со сторонами: AB / A’B’ = AC / A’C’ = BC / B’C’.

Математики рекомендуют отметить некоторую точку C» относительно стороны AB. Она не должна лежать на последней. Кроме того, расстояния от C и C» до стороны AB должны быть эквивалентны. Иными словами, следует построить ΔABС», который является «зеркальным» отображением ΔABC относительно его стороны AB. Если AB / A’B’ = AC» / A’C’, то ΔABC» ∼ ΔA’B’C’ по I признаку.

Следующий шаг — доказательство равенства ΔABC и ΔABC». Они равны по двум сторонам AC = AC» и BC = BC». Следовательно, ΔABC ∼ ΔA’B’C’ подобные.

Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Теорема об отношении площадей

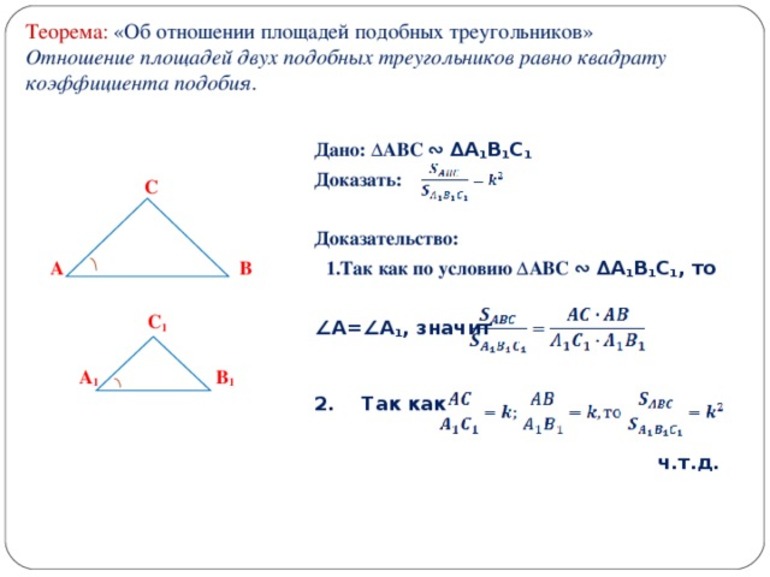
Для решения задач специалисты рекомендуют применять еще теорему об отношении площадей. Обязательным условием ее использования являются ΔABC ∼ ΔA’B’C’ с коэффициентом подобия «k». Ее формулировка имеет такой вид: величина отношения площадей двух подобных треугольников прямо пропорциональна квадрату гомотетии.

Исходя из равенства углов ∠ВАС = ∠B’A’C’ можно записать такое соотношение, в котором тригонометрическая функция не учитывается, поскольку при делении равных коэффициентов получается 1: S / S’ = (AB * AC) / (A’B’ * A’C’). По свойству произведения дробей верно такое преобразование: (AB / A’B’) * (AC / A’C’) = k * k = k 2 . Утверждение доказано полностью.

Видео:59. Определение подобных треугольниковСкачать

Некоторые свойства и следствия

Математики также считают, что используя некоторые свойства и следствия из теорем, можно расширить возможности по решению задач. Свойства подобных треугольников можно применять и к другим плоским или объемным фигурам. Следствия классифицируются на несколько типов:

Отношение площадей плоских фигур прямо пропорционально квадрату их k.
Куб коэффициента подобия прямо пропорционален объему большей фигуры и обратно пропорционален объему меньшей: V / V’ = k 3 .
Коэффициент «k» эквивалентен отношению периметров (P), а также биссектрис, медиан, высот и перпендикуляров, которые являются серединными.
В прямоугольном Δ длина высоты, опущенной на гипотенузу, эквивалентна среднему геометрическому двух проекций на соответствующий катет. Если она опущена из прямого ∠, то значит делит фигуру на подобные Δ по I признаку.
Величина катета эквивалентна средней величине в геометрической интерпретации гипотенузы и произведению проекции катета на гипотенузу.

Например, второе свойство можно применить для решения такого упражнения: дан объем большего конуса V = 125 м 3 , а необходимо найти значение V’ для малого, зная коэффициент k, который равен 3. Задача решается очень просто: V’ = [V]^(1/3) = [125]^(1/3) = 5 (м 3 ).

Видео:8 класс, 20 урок, Определение подобных треугольниковСкачать

Пример решения

Существуют множество типов задач, однако наиболее часто попадаются такие, в которых необходимо доказать, что фигуры являются подобными. Стороны ΔABC равны таким значениям: 10, 12 и 25. Кроме того, существует еще ΔA’B’C’ со сторонами 5, 6 и 10. Фигуры не имеют точек пересечения. Необходимо доказать их подобие.

Для решения рисунок чертить необязательно, поскольку для доказательства необходимо применение не геометрического метода, а алгебраического. Следует ввести обозначения для ΔABC: AB = 10, BC = 12 и AC = 25. Аналогичную процедуру необходимо сделать для ΔA’B’C’: сторона A’B’ равна числу 5, B’C’ = 6 и A’C’ = 10.

Далее нужно вычислить коэффициент k для каждой из сторон: k1 = AB / A’B’ = 10 / 5 = 2, k2 = BC / B’C’ = 12 / 6 = 2 и k3 = AC / A’C’ = 25 / 10 = 2,5. Из соотношений следует, что фигуры не являются подобными, поскольку не выполняется такое равенство: k = k1 = k2 = k3. Для наглядности можно построить также таблицу со значениями коэффициентов.

Таким образом, для решения задач по нахождению параметров подобных треугольников необходимо знать признаки подобия, а также некоторые свойства, которые рекомендуют использовать специалисты-математики.

Видео:Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Подобные треугольники

Видео:Подобные треугольники - 8 класс геометрияСкачать

Определение

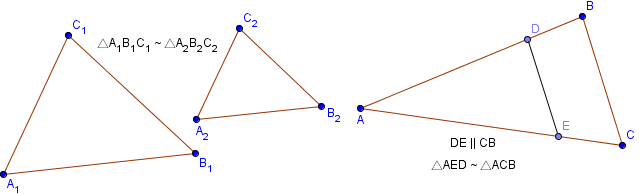
Как правило, два треугольника считаются подобными если они имеют одинаковую форму, даже если они различаются размерами, повернуты или даже перевернуты.

Математическое представление двух подобных треугольников A₁B₁C₁ и A₂B₂C₂ , показанных на рисунке, записывается следующим образом:

Два треугольника являются подобными если:

1. Каждый угол одного треугольника равен соответствующему углу другого треугольника:
∠A₁ = ∠A₂, ∠B₁ = ∠B₂ и∠C₁ = ∠C₂

2. Отношения сторон одного треугольника к соответствующим сторонам другого треугольника равны между собой:
$frac =frac =frac$

3. Отношения двух сторон одного треугольника к соответствующим сторонам другого треугольника равны между собой и при этом
углы между этими сторонами равны:
$frac=frac $ и $angle A_1 = angle A_2$
или
$frac =frac$ и $angle B_1 = angle B_2$
или
$frac=frac$ и $angle C_1 = angle C_2$

Не нужно путать подобные треугольники с равными треугольниками. У равных треугольников равны соответствующие длины сторон. Поэтому для равных треугольников:

Из этого следует что все равные треугольники являются подобными. Однако не все подобные треугольники являются равными.

Несмотря на то, что вышеприведенная запись показывает, что для выяснения, являются ли два треугольника подобными или нет, нам должны быть известны величины трех углов или длины трех сторон каждого треугольника, для решения задач с подобными треугольниками достаточно знать любые три величины из указанных выше для каждого треугольника. Эти величины могут составлять различные комбинации:

1) три угла каждого треугольника (длины сторон треугольников знать не нужно).

Или хотя бы 2 угла одного треугольника должны быть равны 2-м углам другого треугольника.
Так как если 2 угла равны, то третий угол также будет равным.(Величина третьего угла составляет 180 — угол1 — угол2)

2) длины сторон каждого треугольника (углы знать не нужно);

3) длины двух сторон и угол между ними.

Далее мы рассмотрим решение некоторых задач с подобными треугольниками. Сначала мы рассмотрим задачи, которые можно решить непосредственным использованием вышеуказанных правил, а затем обсудим некоторые практические задачи, которые решаются по методу подобных треугольников.

Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Практические задачи с подобными треугольниками

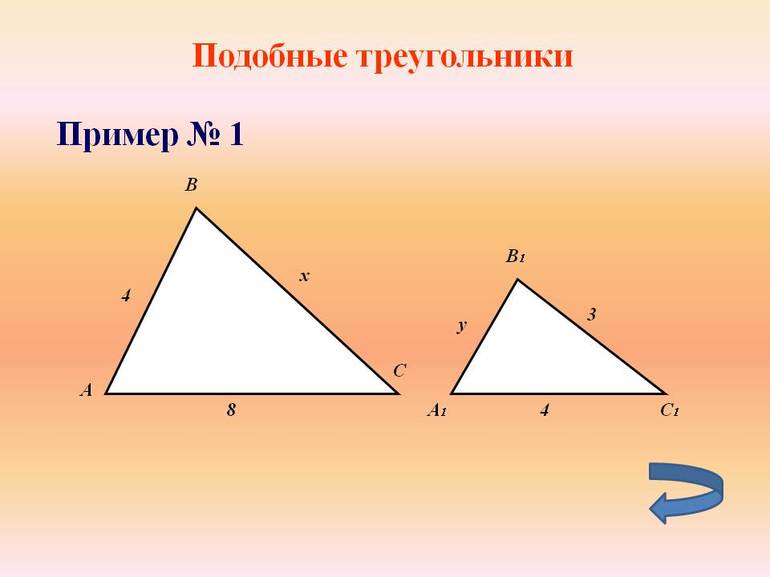
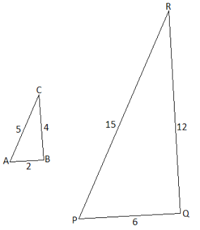
Пример №1: Покажите, что два треугольника на рисунке внизу являются подобными.

Решение:
Так как длины сторон обоих треугольников известны, то здесь можно применить второе правило:

Пример №2: Покажите, что два данных треугольника являются подобными и определите длины сторон PQ и PR.

Решение:
∠A = ∠P и ∠B = ∠Q, ∠C = ∠R(так как ∠C = 180 — ∠A — ∠B и ∠R = 180 — ∠P — ∠Q)

Из этого следует, что треугольники ΔABC и ΔPQR подобны. Следовательно:
$frac=frac=frac$

Пример №3: Определите длину AB в данном треугольнике.

Решение:

∠ABC = ∠ADE, ∠ACB = ∠AED и ∠A общий => треугольники ΔABC и ΔADE являются подобными.

$frac = frac = frac = frac = frac = frac Rightarrow 2times AB = AB + 4 Rightarrow AB = 4$

Пример №4:Определить длину AD (x) геометрической фигуры на рисунке.

Треугольники ΔABC и ΔCDE являются подобными так как AB || DE и у них общий верхний угол C.
Мы видим, что один треугольник является масштабированной версией другого. Однако нам нужно это доказать математически.

AB || DE, CD || AC и BC || EC
∠BAC = ∠EDC и ∠ABC = ∠DEC

Исходя из вышеизложенного и учитывая наличие общего угла C, мы можем утверждать, что треугольники ΔABC и ΔCDE подобны.

Следовательно:
$frac = frac = frac = frac Rightarrow CA = frac = 23.57$
x = AC — DC = 23.57 — 15 = 8.57

Практические примеры

Пример №5: На фабрике используется наклонная конвеерная лента для транспортировки продукции с уровня 1 на уровень 2, который выше уровня 1 на 3 метра, как показано на рисунке. Наклонный конвеер обслуживается с одного конца до уровня 1 и с другого конца до рабочего места, расположенного на расстоянии 8 метров от рабочей точки уровня 1.

Фабрика хочет модернизировать конвеер для доступа к новому уровню, который находится на расстоянии 9 метров над уровнем 1, и при этом сохранить угол наклона конвеера.

Определите расстояние, на котором нужно установить новый рабочий пункт для обеспечения работы конвеера на его новом конце на уровне 2. Также вычислите дополнительное расстояние, которое пройдет продукция при перемещении на новый уровень.

Решение:

Для начала давайте обозначим каждую точку пересечения определенной буквой, как показано на рисунке.

Исходя из рассуждений, приведенных выше в предыдущих примерах, мы можем сделать вывод о том, что треугольники ΔABC и ΔADE являются подобными. Следовательно,

$frac = frac = frac = frac Rightarrow AB = frac = 24 м$
x = AB — 8 = 24 — 8 = 16 м

Таким образом, новый пункт должен быть установлен на расстоянии 16 метров от уже существующего пункта.

А так как конструкция состоит из прямоугольных треугольников, мы можем вычислить расстояние перемещения продукции следующим образом:

Аналогично, $AC = sqrt = sqrt = 25.63 м$
что является расстоянием, которое проходит продукция в данный момент при попадании на существующий уровень.

y = AC — AE = 25.63 — 8.54 = 17.09 м
это дополнительное расстояние, которое должна пройти продукция для достижения нового уровня.

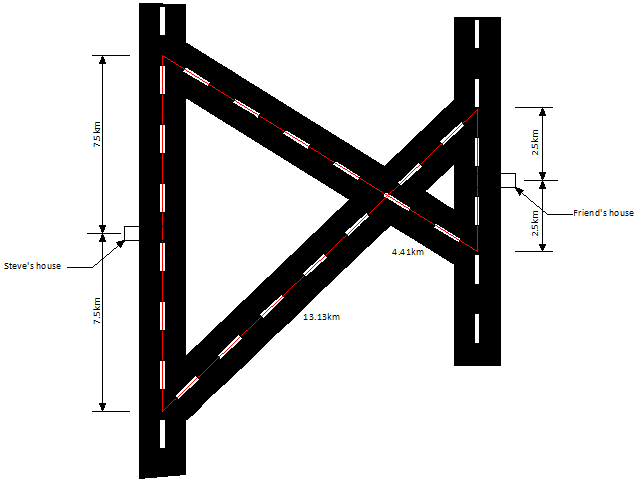
Пример №6: Стив хочет навестить своего приятеля, который недавно переехал в новый дом. Дорожная карта проезда к дому Стива и его приятеля вместе с известными Стиву расстояниями показана на рисунке. Помогите Стиву добраться к дому его приятеля наиболее коротким путем.

Решение:

Дорожную карту можно геометрически представить в следующем виде, как показано на рисунке.

Мы видим, что треугольники ΔABC и ΔCDE подобны, следовательно:
$frac = frac = frac$

В условии задачи сказано, что:

AB = 15 км, AC = 13.13 км, CD = 4.41 км и DE = 5 км

Используя эту информацию, мы можем вычислить следующие расстояния:

Стив может добраться к дому своего друга по следующим маршрутам:

A -> B -> C -> E -> G, суммарное расстояние равно 7.5+13.23+4.38+2.5=27.61 км

F -> B -> C -> D -> G, суммарное расстояние равно 7.5+13.23+4.41+2.5=27.64 км

F -> A -> C -> E -> G, суммарное расстояние равно 7.5+13.13+4.38+2.5=27.51 км

F -> A -> C -> D -> G, суммарное расстояние равно 7.5+13.13+4.41+2.5=27.54 км

Следовательно, маршрут №3 является наиболее коротким и может быть предложен Стиву.

Пример 7:
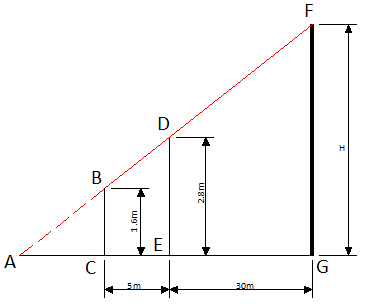
Триша хочет измерить высоту дома, но у нее нет нужных инструментов. Она заметила, что перед домом растет дерево и решила применить свою находчивость и знания геометрии, полученные в школе, для определения высоты здания. Она измерила расстояние от дерева до дома, результат составил 30 м. Затем она встала перед деревом и начала отходить назад, пока верхний край здания стал виден над верхушкой дерева. Триша отметила это место и измерила расстояние от него до дерева. Это расстояние составило 5 м.

Высота дерева равна 2.8 м, а высота уровня глаз Триши равна 1.6 м. Помогите Трише определить высоту здания.