Все элементы треугольника 7 класс (3 видео)

Треугольник. Медиана, биссектриса, высота, средняя линия.

Содержание

теория по математике 📈 планиметрия
Виды треугольников по углам
Виды треугольников по сторонам
Медиана, биссектриса, высота, средняя линия треугольника
Медиана
Биссектриса
Высота
Средняя линия
Все элементы треугольника 7 класс
Опорный конспект «Треугольники»
Треугольники
💡 Видео

теория по математике 📈 планиметрия

Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.

Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.

Виды треугольников по углам

Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.

Остроугольные	Тупоугольные	Прямоугольные
Остроугольным треугольником называется треугольник, у которого все три угла острые. На рисунке показан такой остроугольный треугольник АВС.	Тупоугольным называется треугольник, у которого есть тупой угол. В треугольнике может быть только один тупой угол. На рисунке показан треугольник такого вида, где угол М – тупой.	Прямоугольным называется треугольник, у которого есть угол, равный 90 0 (прямой угол). На рисунке угол С равен 90 0 . Такой угол в любом прямоугольном треугольнике – единственный.

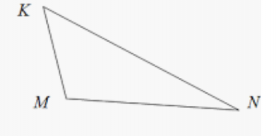Виды треугольников по сторонам

Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.

Разносторонний	Равнобедренный	Равносторонний
Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС.	Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС.	Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС.

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Медиана, биссектриса, высота, средняя линия треугольника

Медиана

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.

По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.

Биссектриса

Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.

В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD₁, EE₁ и CC₁.

По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.

Высота

Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.

На рисунке показаны высоты треугольника АВС: АН₁, ВН₂ и СН₃.

По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.

Средняя линия

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.

Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.

Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.

При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 90 0 .

Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.

Составим отношение сторон:

A E A B . . = A B A F . . откуда по свойству пропорции АВ 2 =АЕ ∙ АF

Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.

Составим отношение сторон:

A E A D . . = A C A F . . ; откуда выразим AD= A E ∙ A F А C . . = A E ∙ A F A C . .

Теперь рассмотрим наши два полученных равенства: АВ 2 =АЕ ∙ АF и AD= A E ∙ A F A C . .

Видим, что 36 2 =АЕ ∙ АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD= A E ∙ A F A C . . = 36 2 54 . . = 24

Теперь найдем CD=AC-AD=54-24=30

pазбирался: Даниил Романович | обсудить разбор | оценить

На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.

Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.

pазбирался: Даниил Романович | обсудить разбор | оценить

В треугольнике АВС известно, что угол ВАС равен 84 0 , АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0

pазбирался: Даниил Романович | обсудить разбор | оценить

Видео:Треугольники. 7 класс.Скачать

Все элементы треугольника 7 класс

Треугольники: равные, равнобедренные. Первый, второй и третий признаки равенства треугольников. Перпендикуляр, высота, медиана, биссектриса, основание, вершина, боковая сторона. Свойства и признаки равнобедренного треугольника. Серединный перпендикуляр, геометрическое место точек, первая замечательная точка. Подробные доказательства теорем.

Наглядная геометрия 7 класс. Опорный конспект № 2 «Треугольники».

Треугольник — одна из самых замечательных и самых важных фигур в геометрии. Все знают, как он выглядит. Но что же такое треугольник? Допустим, что треугольник — это замкнутая ломаная из трех звеньев. Можно представить себе треугольник, сделанный из проволоки. Но известно, что у него есть площадь. Поэтому треугольник — это трехзвенная замкнутая ломаная вместе с частью плоскости, которую она ограничивает. Представьте себе треугольник, сделанный из фанеры или вырезанный из картона.

Очень важным моментом при решении геометрических задач является нахождение равных треугольников. Очевидно, что если у двух треугольников все стороны и углы окажутся соответственно равными, то и треугольники будут равны. На практике равные треугольники определяют, прикладывая их друг к другу. Если треугольники совпадут при наложении, значит, они равны. Этот способ и позволяет дать определение равных треугольников.

Но вот, допустим, у каждого из двух треугольников есть две стороны, которые равны 5 см и 6 см, и какой-то из углов равен 50°. Можно ли утверждать, что треугольники равны? Оказывается, нет. На рисунке вы видите два треугольника с указанными размерами. Они не равны.

При каких же минимальных условиях треугольники будут равны? Существуют по крайней мере три признака равенства треугольников, когда по равенству некоторых сторон и углов можно абсолютно точно сказать, что они равны. Например, если бы угол 50° был образован сторонами длиной 5 см и 6 см, то треугольники были бы равны между собой.

Опорный конспект «Треугольники»

Треугольник — это трехзвенная замкнутая ломаная вместе с частью плоскости, которую она ограничивает. Сумма длин всех трех сторон треугольника называется периметром. Треугольники называются равными, если совпадают при наложении. Если равные треугольники наложить так, что они совпадут, то окажется, что в равных треугольниках против равных сторон лежат равные углы, а против равных углов лежат равные стороны.

Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Действительно, если наложить треугольники друг на друга равными углами, то совпадут и равные стороны. Значит, совпадут и оставшиеся две вершины.

Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Если наложить треугольники друг на друга равными сторонами, то совпадут углы, прилежащие к этим сторонам. Значит, совпадут и третьи вершины.

Перпендикуляром, опущенным из данной точки на данную прямую, называется отрезок прямой, перпендикулярной данной, проходящей через данную точку, с концами в данной точке и в точке пересечения с данной прямой. Точка пересечения называется основанием перпендикуляра.

Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону или ее продолжение.

Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, заключенный между вершиной и точкой пересечения биссектрисы угла и стороны треугольника.

Треугольник, у которого две стороны равны, называется равнобедренным. Равные стороны называются боковыми сторонами, третья сторона — основанием, вершина напротив этой стороны — вершиной равнобедренного треугольника. Причем названия «основание», «боковые стороны» и «вершина» равнобедренного треугольника сохраняются, как бы треугольник ни был расположен.

Свойства равнобедренного треугольника. 1. В равнобедренном треугольнике углы при основании равны. 2. Биссектриса равнобедренного треугольника, проведенная из вершины к основанию, является высотой и медианой.

Признак равнобедренного треугольника (по двум углам). Если в треугольнике два угла равны, то он равнобедренный.

Есть еще три признака равнобедренного треугольника. Треугольник является равнобедренным, если:

высота треугольника является и медианой;
высота треугольника является и биссектрисой;
медиана треугольника является и биссектрисой (доказывается продлением медианы на ее длину).

Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Серединным перпендикуляром к отрезку называется прямая, перпендикулярная этому отрезку и проходящая через его середину.

Свойство точек серединного перпендикуляра. Любая точка серединного перпендикуляра равноудалена от концов отрезка. Если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.

Геометрическое место точек (ГМТ) — это множество всех точек плоскости, обладающих общим свойством. Например, все точки серединного перпендикуляра равноудалены от концов отрезка, и все точки плоскости, равноудаленные от концов отрезка, лежат на серединном перпендикуляре.

Первая замечательная точка. Все три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке — центре описанной окружности.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Треугольники

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке впервые познакомимся с треугольником – важнейшей фигурой геометрии, строить которую в режиме онлайн научит педагог. Вначале дается определение треугольника и его основных элементов: вершин, сторон, углов. Далее рассматривается понятие равных треугольников. В конце урока разбираются задачи, посвященные противолежащим углу сторонам, прилежащим углам, взаимосвязи элементов и расчёта периметра.