Вписанный квадрат в окружность задачи огэ (7 видео)

Вписанная и описанная окружность (квадрат) Задание №16 ОГЭ

27 мартаНет отметокЗдравствуйте, уважаемые читатели. Продолжаем разбор заданий с окружностью. В этой статье рассмотрим задачи на вписанную окружность в квадрат и описанную около квадрата.

4. Вписанная и описанная окружность (квадрат)

Все задачи такого типа достаточно простые. Приступим сразу же к решению задач.

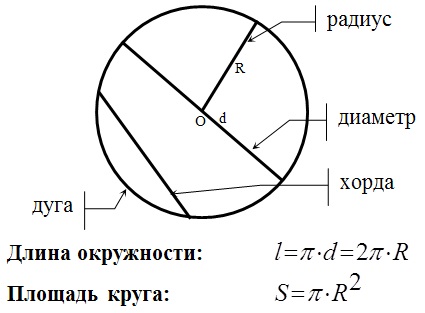
Радиус окружности – это отрезок, соединяющий центр окружности с любой точкой лежащей на окружности.

Решение к этой задачи представлю в виде картинки.

О – центр окружности, r – радиус окружности. В этой задаче радиус окружности равен половине стороны квадрата. Ответ 8.

Найдите площадь квадрата, описанного вокруг окружности радиуса 9

Задача обратная той, что мы решили выше. Так как радиус окружности равен 9, то сторона квадрата равна 18. Площадь квадрата равна:

В предыдущих задачах мы определили, что если известен радиус вписанной окружности в квадрат, то сторона квадрата будет равна удвоенному значению радиуса.

Зная сторону квадрата, диагональ квадрата найдем используя теорему Пифагора.

Эта задача, включает в себя все этапы, которые были разобраны выше. Задачу можно разбить на действия:

1) Найдем сторону квадрата.

2) Найдем ди квадрата.

3) Найдем радиус описанной окружности, разделив диаметра квадрата пополам.

1) Найдем сторону квадрата:

2) Найдем диаметр квадрата используя теорему Пифагора:

3) Найдем радиус описанной окружности, разделив диаметра квадрата пополам.

Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.

Содержание

Вписанный квадрат в окружность задачи огэ
Задание №16 ОГЭ по математике
Теория к заданию №16
🎥 Видео

Видео:Геометрия с нуля! / Выпуск № 6. Формула квадрата, вписанного в окружность / ОГЭ по математике 2022Скачать

Вписанный квадрат в окружность задачи огэ

Сторона квадрата равна 10. Найдите его площадь.

Площадь квадрата равна квадрату его стороны, поэтому она равна 100.

Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.

Площадь получившейся фигуры равна разности площадей квадрата и прямоугольника: 6 · 6 − 4 · 2 = 28.

Периметр квадрата равен 160. Найдите площадь квадрата.

Все стороны квадрата равны, поэтому сторона длина стороны квадрата равна Найдём площадь квадрата как квадрат его стороны:

Видео:Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Задание №16 ОГЭ по математике

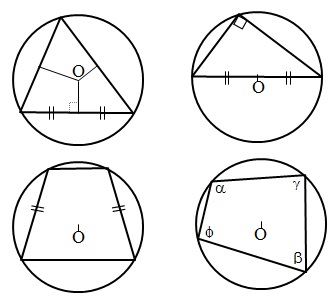
В 16 задании ОГЭ по математике необходимо решить простую задачу по геометрии. Для успешного решения необходимо обладать базовыми знаниями по геометрии вообще, так как сложно выделить какую-то одну тему, по которой даны задания. Это относится ко всему модулю геометрии. Я рекомендую повторить понятия центральные и вписанные углы, свойства касательных к окружности, взаимосвязь между радиусом описанной или вписанной окружности в геометрические фигуры — в первую очередь прямоугольный треугольник и квадрат.

Теория к заданию №16

Несмотря на то, что в задании №16 могут потребоваться любые знания по геометрии, в данном разделе мы разберем теорию по теме «окружность».

Начнем рассмотрение с понятия вписанная окружность:

Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
Если окружность вписана в произвольный четырехугольник, тогда попарные суммы противолежащих сторон равны между собой: a + b = c + d

Длинна окружности и площадь: Касательная и секущая:

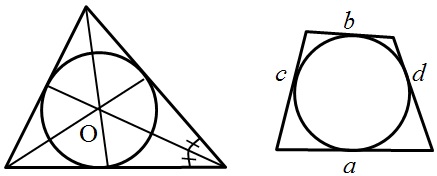
Касательная – прямая, имеющая с окружностью одну общую точку.
Секущая – прямая, имеющая с окружностью две общие точки.

Описанная окружность и её свойства:

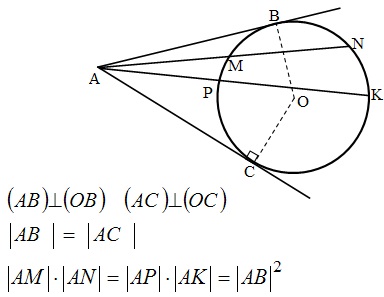
Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его трем сторонам.
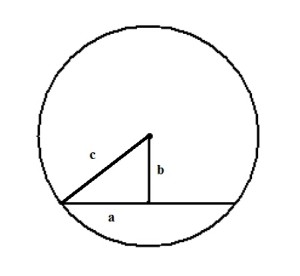
Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.
Около трапеции можно описать окружность только тогда, когда трапеция равнобочная.
Если окружность описана около произвольного четырехугольника, тогда попарные суммы противолежащих углов равны между собой.

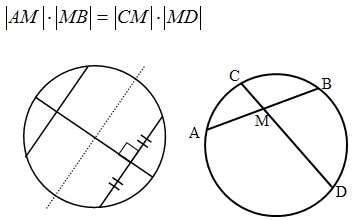
Хорда – отрезок, соединяющий две точки окружности.

Диаметр, делящий хорду пополам, перпендикулярен хорде.
В окружности равные хорды равноудалены от центра окружности.
Отрезки пересекающихся хорд связаны равенством:

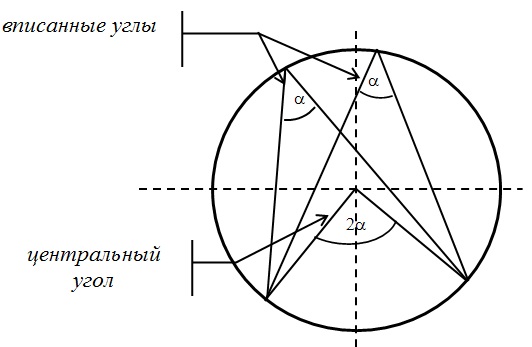
Центральный и вписанный углы:

Ниже я разобрал три различных примера 10 задания. Если у вас остались пожелания, или вы хотите разобрать задачу, которой здесь нет, напишите об этом в комментарии.

Внимательно посмотрим на рисунок. Угол ABC опирается на дугу ADC, а угол CAD — на дугу DC. Угол, который нам необходимо найти — ABD, опирается на дугу AD — которая является частью дуги ADC за вычетом дуги DC. Значит, угол ABD равен разности углов ABC и CAD:

∠ABD = 92 — 60 = 32

pазбирался: Даниил Романович | обсудить разбор | оценить

Во-первых, касательные равны между собой по длине, а значит треугольник с основанием AB равнобедренный. Угол при вершине этого треугольника равен 2 градуса по условию, значит углы при основании равны:

Во-вторых, касательные перпендикулярны радиусу, то есть угол между ними и радиусом равен 90 градусов.

Заметим, что угол ABO, который необходимо найти, является частью угла между касательной и радиусом, а именно за вычетом угла, который мы нашли в первом пункте. Значит, этот угол равен:

pазбирался: Даниил Романович | обсудить разбор | оценить

Для решения необходимо вспомнить, что центр описанной около прямоугольного треугольника окружности расположен в середине гипотенузы. То есть гипотенуза является диаметром, а её половина — радиусом.

По теореме Пифагора найдем гипотенузу AB:

AB² = BC² + AC² = 12² + 16² = 144 + 256 = 400

Гипотенуза равна 20, значит радиус — 10.

pазбирался: Даниил Романович | обсудить разбор | оценить

Для решения данной задачи необходимо провести радиус окружности к точке начала хорды:

Получаем прямоугольный треугольник, где гипотенуза c — радиус и равна 13 см, b — расстояние до хорды — 5 см. По теореме Пифагора находим катет a: a² + b² = c² a² = c² — b² = 13² — 5² = 169 — 25 = 144 Откуда а = √144 = 12 Но а — лишь половина хорды, поэтому вся

Хорда — длинный эластичный продольный тяж у хордовых животных; осевой скелет их предковых и некоторых современных форм. Тянется вдоль тела ниже центральной нервной системы и выше полости тела.

pазбирался: Даниил Романович | обсудить разбор | оценить

Сторона АВ треуг-ка АСВ является диаметром окружности. Это означает, что угол АСВ опирается на диаметр. Тогда угол АСВ равен 90 0 , и, следовательно, ∆АСВ прямоугольный. Если ∆АСВ прямоугольный, то для нахождения одной из его сторон можно применить т.Пифагора. По т.Пифагора

АС 2 +ВС 2 =АВ 2 (1)

По условию АС=16, радиус окружности R=10. Если R=10, то АВ=2R=2·10=20. Тогда из (1) получим: 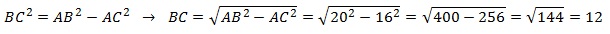Ответ: 12

pазбирался: Даниил Романович | обсудить разбор | оценить

Поскольку вершина О угла АОВ лежит в центре окружности, значит, этот угол центральный. А если так, то он равен величине дуги АВ. Т.е. ᴗАВ=113 0 . Угол АСВ является вписанным. Следовательно, его величина равна половине дуги, на которую он опирается. Из рисунка видно, что оба угла (АОВ и АСВ) опираются на одну и ту же дугу. Т.к. ᴗАВ=113 0 , то угол АСВ равен

0,5 · ᴗАВ = 0,5 · 113 0 = 56,5 0 .

pазбирался: Даниил Романович | обсудить разбор | оценить

Радиус вписанной в квадрат окружности равен 22 √ 2 . Найти диагональ этого квадрата.

Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.

Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22 √ 2 , то сторона квадрата будет в два раза больше, т.е. 44 √ 2 .

Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44 √ 2 . Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а √ 2 , где с – гипотенуза, а – катет. Подставим в неё наши данные:

с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88

pазбирался: Даниил Романович | обсудить разбор | оценить