Вписанный и центральный угол окружности тренажер

Тренажер по геометрии для 8-9 классов с краткой справочной информацией. В архиве четыре варианта с ответами.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Скачать:

Хочешь подготовиться к ЕГЭ за 1450 ₽ в месяц?

Вебинары Учи.Дома помогут подготовиться к ЕГЭ 2022. Поддерживающее коммьюнити из классных преподавателей, которые состоят в комиссии и знают особенности заданий изнутри. Хочешь попробовать бесплатно? Кликай по кнопке!

попробовать бесплатно, онлайн, 40 минут

Видео:Вписанные и центральные углы #огэ #огэматематика #математикаСкачать

Предварительный просмотр:

Вариант 1Вписанные и описанные углы

2. ОА=ОВ=ОС – радиус

5. AOB – центральный

6. AСB – вписанный

1. Найдите градусную меру угла:

2. Найдите градусную меру дуги:

3. Точка О — центр окружности, AСB= 25 º (см. рисунок). Найдите величину AOB (в градусах).

4. Точка О — центр окружности, СAB= 35 º (см. рисунок). Найдите величину ACB (в градусах).

5. Точка О — центр окружности, градусная мера меньшей из дуг AB равна 128 º , СDB= 46 º (см. рисунок). Найдите величину DCA (в градусах).

Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

По теме: методические разработки, презентации и конспекты

Вписанные и центральные углы

Активизация самостоятельности познавательной деятельности учащихся. Формирование навыков коллективной работы, развитие чувства ответственности за свои знания.

Разработка урока «Вписанные и центральные углы» 8 класс

Данная разработка включает в себя конспект урока, презентацию к уроку, самостоятельную работу, тест.

Вписанные и центральные углы

«Вписанные и центральные углыУрок изучения нового материала с применением мультимедийной презентации.

Тест по геометрии «Вписанные и центральные углы»

Тест по геометрии для учащихся 8 класса состоит из 12 заданий: выбор одного из предложенных ответов, краткая запись ответа, соответствие. На последний слайд выводится результат о решённых заданиях и в.

«Окружность. Вписанные и центральные углы.»

Презентация к уроку геометрии 8 -го класса. Материал может быть использован как в 8 классе, так и в 9 классе при подготовке к ОГЭ.

Урок по геометрии «Вписанные и центральные углы» 8 класс

Урок подготовки учащихся к успешной сдачи ОГЭ.

Тест по теме «Вписанные и центральные углы».

Тест по теме «Вписанные и центральные углы». Предназначен для повторения темы «Вписанные и центральные углы» при подготовке к ОГЭ. Состоит из 7 заданий для 2 вариантов.

Видео:Вписанные и центральные углыСкачать

Тренажер по теме «Центральные и вписанные углы»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:ЦЕНТРАЛЬНЫЙ угол ВПИСАННЫЙ угол окружности 8 класс АтанасянСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Тренажер по теме «Центральные и вписанные углы»

В угол C величиной 79° вписана окружность, которая касается сторон угла в точках A и B , точка O — центр окружности. Найдите угол AOB . Ответ дайте в градусах.

В окружности с центром O AC и BD — диаметры. Центральный угол AOD равен 122°. Найдите вписанный угол ACB . Ответ дайте в градусах.

Точка O — центр окружности, на которой лежат точки A, B и C . Известно, что ∠ ABC = 86° и ∠ OAB = 28°. Найдите угол BCO . Ответ дайте в градусах.

AC и BD — диаметры окружности с центром O . Угол ACB равен 53°. Найдите угол AOD . Ответ дайте в градусах.

На окружности с центром O отмечены точки A и B так, что Длина меньшей дуги AB равна 63. Найдите длину большей дуги.

AC и BD — диаметры окружности с центром O . Угол ACB равен 18°. Найдите угол AOD . Ответ дайте в градусах.

В угол величиной 157° вписана окружность, которая касается сторон угла в точках и , точка — центр окружности. Найдите угол . Ответ дайте в градусах.

Треугольник ABC вписан в окружность с центром в точке O . Точки O и C лежат в одной полуплоскости относительно прямой AB Найдите угол ACB , если угол AOB равен 47°. Ответ дайте в градусах

К окружности с центром в точке О проведены касательная AB и секущая AO . Найдите радиус окружности, если AB = 24 , AO = 26 .

Краткое описание документа:

Тренажер по теме «Центральные и вписанные углы». Отработка навыков, необходимых для сдачи основного государственного экзамена. Для подготовки тренажера использовались ресурсы сайта https://oge.sdamgia.ru/. Работа состоит из девяти задание, направленных на формирование умений вычислять градусные меры центральных и вписанных углов.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 949 человек из 80 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 325 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 698 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 483 618 материалов в базе

Материал подходит для УМК

«Геометрия. 7-9 класс», Волович М.Б., Атанасян Л.С.

Глава 4. Окружность

Видео:Всё про вписанные и центральные углы за 4 минуты | Борис Трушин |Скачать

Дистанционные курсы для педагогов

Другие материалы

• 29.03.2020
• 156

• 29.03.2020
• 148

• 28.03.2020
• 212

• 28.03.2020
• 8062

• 28.03.2020
• 82

• 26.03.2020
• 123

• 26.03.2020
• 330

• 26.03.2020
• 170

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 29.03.2020 1134 —> —> —> —>
• DOCX 80 кбайт —> —>
• Оцените материал:

Настоящий материал опубликован пользователем Козинкова Светлана Владимировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет и 2 месяца
• Подписчики: 0
• Всего просмотров: 80846
• Всего материалов: 68

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Углы, вписанные в окружность. 9 класс.Скачать

Дистанционные курсы
для педагогов

548 курсов от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Первые результаты по сокращению отчетности у учителей ожидаются осенью

Время чтения: 1 минута

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

Число иностранных студентов в РФ увеличилось за три года

Время чтения: 1 минута

Первый мониторинг вузов РФ по новым показателям пройдёт в 2023 году

Время чтения: 2 минуты

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В Петербурге дали рекомендации по переводу школьников на дистант

Время чтения: 3 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:ВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный УголСкачать

Вписанный и центральный угол окружности тренажер

Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен 60°. Найдите радиус окружности.

Рассмотрим треугольник AOB: он равнобедренный, его боковые стороны равны радиусу.

Углы при основании равнобедренного треугольника равны. Пусть AOB равен x, тогда x + 60° + 60° = 180°, где x = 60°. Треугольник, у которого все углы равны, — равносторонний треугольник; значит, радиус равен 6.

В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB.

Вписанные углы ВСD и ВАD опираются на одну и ту же дугу окружности, поэтому они равны. Тем самым, угол OAB = 30°.

Найдите градусную меру центрального ∠MON, если известно, NP — диаметр, а градусная мера ∠MNP равна 18°.

Треугольник MON — равнобедренный. Тогда ∠MON = 180° − 2·18° = 144°.

Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.

Дуга FD, не содержащая точку Е, равна 360° − 150° − 68° = 142°, поэтому ∠DEF = 71°.

Найдите градусную меру ∠ACB, если известно, что BC является диаметром окружности, а градусная мера центрального ∠AOC равна 96°.

Так как ∠AOC и ∠AOB — смежные, ∠AOB = 180° − ∠AOC = 84°. Центральный угол равен дуге, на которую он опирается, поэтому градусная мера дуги AB равна 84°. Угол ACB — вписанный и равен половине дуги, на которую опирается, поэтому ∠ACB = 42°.

Приведем решение Артура Ахметьянова.

Треугольник AOC равнобедренный, поскольку AO = OC как радиусы окружности, тогда

💡 Видео

Геометрия. Окружность. Вписанные и центральные углы 1. Тренажёр ОГЭ.Скачать

Геометрия. Окружность. Вписанные и центральные углы 2. Тренажёр ОГЭ.Скачать

Центральный угол в окружностиСкачать

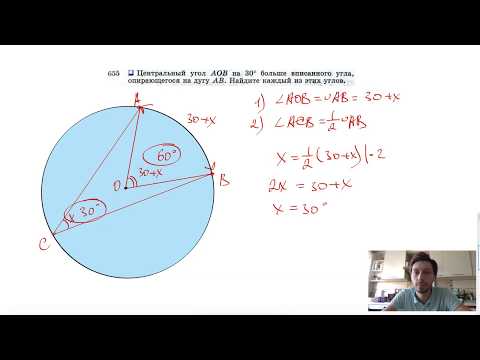
№655. Центральный угол АОВ на 30° больше вписанного угла, опирающегося на дугу АВ. НайдитеСкачать

Вписанные углы в окружностиСкачать

ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ . §9 геометрия 8 классСкачать

8 класс, 34 урок, Теорема о вписанном углеСкачать

Вписанные и центральные углыСкачать

Геометрия. Теорема о вписанном углеСкачать

Решение задач на тему центральные и вписанные углы.Скачать

Вписанный угол, который опирается на диаметрСкачать

Как понять центральные и вписанные углыСкачать