Вписанные описанные окружности четырехугольник самостоятельная работа

Дидактический материал по теме «Вписанные в окружность четырехугольники. Описанные около окружности четырехугольники.» Данные задачи можно использовать как на закрепление, так и на проверку знаний по теме.

Просмотр содержимого документа
«Дидактический материал по теме «Вписанные в окружность четырехугольники. Описанные около окружности четырехугольники.»»

Дидактический материал по теме «Вписанные в окружность четырехугольники. Описанные около окружности четырехугольники.»

Задача 1. Найдите все углы вписанного в окружность четырехугольника АВСD, если ∠ А=40º, а ∠D =90º

Задача 2. Противоположные стороны четырехугольника, описанного около окружности, равны 7 см и 10 см. Можно ли по этим данным найти периметр четырехугольника?

Задача 3. Сумма сторон AB+CD=18 м. Найти периметр четырехугольника.

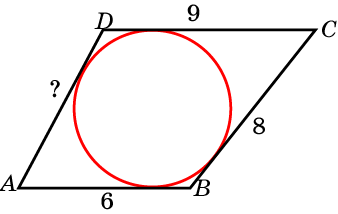
Задача 4. Три последовательные стороны четырехугольника, в который можно вписать окружность, равны 6 см, 8 см и 9 см. Найдите четвертую сторону и периметр этого четырехугольника.

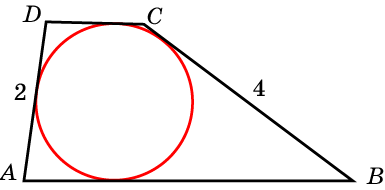
Задача 5. Боковые стороны трапеции, описанной около окружности, равны 2 см и 4 см. Найдите среднюю линию трапеции.

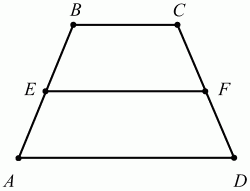
Задача 6. Известно, что в трапецию ABCD с основаниями AD и ВС можно вписать окружность и около неё можно описать окружность, EF – её средняя линия. Известно, что АВ + CD + EF = 18. Найдите периметр трапеции (1)

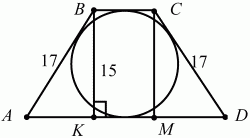
Задача 7. Около окружности с диаметром 15 см описана равнобедренная трапеция с боковой стороной, равной 17 см. Найдите основания трапеции (2)

1. В четырехугольник ABCD вписана окружность, AB = 10, BC = 11 и CD = 15. Найдите четвертую сторону четырехугольника.

Ответ: ___________

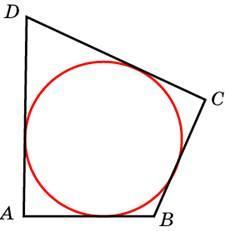
2. Два угла вписанного в окружность четырехугольника равны 84° и 57°. Найдите меньший из оставшихся углов. Ответ дайте в градусах.

Ответ: ___________

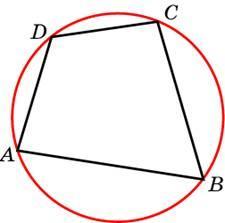
3. В четырехугольник ABCD вписана окружность, AB = 10, CD = 16. Найдите периметр четырехугольника.

Ответ: ___________

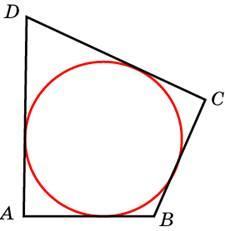
4. Четырехугольник ABCD вписан в окружность. Угол ABD равен 75°, угол CAD равен 35°. Найдите угол ABC. Ответ дайте в градусах.

Ответ: ___________

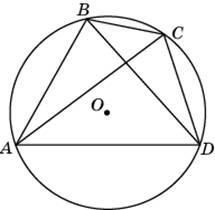
5. Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.

Ответ: ___________

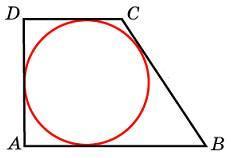
1. В четырехугольник ABCD вписана окружность, AB = 8, BC = 9 и CD = 14. Найдите четвертую сторону четырехугольника.

Ответ: ___________

2. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.

Ответ: ___________

3. В четырехугольник ABCD вписана окружность, AD = 15, BC = 11. Найдите периметр четырехугольника.

Ответ: ___________

4. Четырехугольник ABCD вписан в окружность. Угол ABC равен 105°, угол CAD равен 35°. Найдите угол ABD. Ответ дайте в градусах.

Ответ: ___________

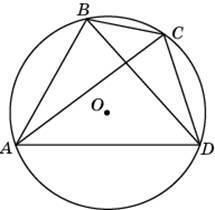
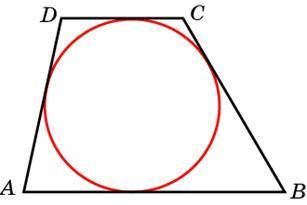
5. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.

Ответ: ___________

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Тема «Самостоятельная работа. Вписанные четырехугольники»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Определение четырехугольника, вписанного в окружность.

Центр окружности , описанной около четырехугольника лежит на …

Около какого четырехугольника можно описать окружность.

4.Свойство противолежащих сторон описанного четырехугольника.

5. Можно ли около ромба описать окружность.

6. Среди приведенных четырехугольников укажите четырехугольник, который может быть вписан в окружность, но не может быть описан около нее

7. Найдите углы вписанного четырехугольника, если два его угла равны 110° и 100°

Определение четырехугольника, описанного около окружности.

Чему равна сумма противолежащих углов вписанного четырехугольника.

При каком условии в четырехугольник можно вписать окружность.

Свойство трапеции, вписанной в четырехугольник.

Можно ли около параллелограмма описать окружность.

6. Среди приведенных четырехугольников укажите четырехугольник, который может быть описан около окружности, но не может быть вписан в нее

Найти сторону описанного около окружности четырехугольника, три последовательные стороны которого равны 5см, 7см, 5см.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 942 человека из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 316 человек из 68 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 691 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 487 737 материалов в базе

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Дистанционные курсы для педагогов

Другие материалы

• 24.05.2017
• 775

• 24.05.2017
• 396

• 24.05.2017
• 571

• 24.05.2017
• 768

• 24.05.2017
• 770

• 24.05.2017
• 306

• 24.05.2017
• 822

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 24.05.2017 2254 —> —> —> —>
• DOCX 21.5 кбайт —> —>
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем БОЙКО ТАТЬЯНА АВКСЕНТЬЕВНА. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 1 месяц
• Подписчики: 0
• Всего просмотров: 24065
• Всего материалов: 31

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:КОНТРОЛЬНАЯ РБ 9 класс Вписанные и описанные окружностиСкачать

Дистанционные курсы
для педагогов

548 курсов от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

«Учителя года» проведут открытые занятия для педагогов России

Время чтения: 1 минута

В Якутске все классы, кроме девятых и одиннадцатых, перейдут на удаленку

Время чтения: 1 минута

В Петербурге дали рекомендации по переводу школьников на дистант

Время чтения: 3 минуты

Пандемия позволила детям получить больше внимания со стороны родителей

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Решение вписанные и описанные четырехугольники для ОГЭ и ЕГЭ
методическая разработка по геометрии (9 класс) на тему

Предложены решения задач из баннка данных для ОГЭ и ЕГЭ. Удобно использовать для коррекции знаний или для учащихся, пропустивших занятия по подготовке к итоговой атттестации

Видео:СРЕДНЯЯ ЛИНИЯ. ТРАПЕЦИЯ. ВПИСАННЫЕ И ОПИСАННЫЕ ЧЕТЫРЕХУГОЛЬНИКИ. Контрольная № 2 Геометрия 8 классСкачать

Скачать:

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Предварительный просмотр:

Окружность, вписанная в многоугольни к http://egemaximum.ru/zadachi-7-mnogougolnik-i-okruzhnost/

Задача 1 . Найдите радиус окружности, вписанной в квадрат со стороной 16.

Решение: Радиус вписанной окружности в квадрат – есть половина стороны квадрата. Поэтому r = 8

Задача 2 . Сторона ромба равна 58, острый угол равен 30˚. Найдите радиус вписанной окружности этого ромба.

Решение: Пусть точки касания окружности противоположных сторон ромба – E и T. Тогда ET– диаметр окружности (точка пересечения диагоналей О – центр симметрии параллелограмма, значит и ромба).

ET – есть расстояние между противоположными сторонами ромба так же, как и высота ромба (DH).

Рассмотрим прямоугольный треугольник ADH. Так как угол А равен 30°по условию, то катет HD, противолежащий этому углу, равен половине гипотенузы AD. То есть HD=ET=29. Значит, радиус вписанной окружности есть ET: 2, то есть 14,5. Ответ: 14,5.

Задача 3 . Найдите высоту трапеции, в которую вписана окружность радиуса 14.

Решение: Высота трапеции – есть диаметр вписанной окружности в трапецию.

h=2r=2·14, h = 28. Ответ:28

Задача 4. Боковые стороны трапеции, описанной около окружности, равны 19 и 13. Найдите среднюю линию трапеции.

Решение: в трапецию вписана окружность, значит BC+AD=AB+CD, что хорошо видно на картинке (равные отрезки помечены согласно свойству отрезков касательных).Итак, BC+AD=32, средняя линия l – есть полусумма оснований, то l =16.

Задача 5. Периметр прямоугольной трапеции, описанной около окружности, равен 80, ее большая боковая сторона равна 30. Найдите радиус окружности

Решение: в трапецию вписана окружность, значит BC+AD=AB+CD и P ABCD =80, то AB+CD= P:2 = 40. CD=30 по условию, то AB=10.

Далее, AB=NQ=2r. r =5. Ответ:5

Задача 6. В четырехугольник ABCD вписана окружность, AB=52, CD=53. Найдите периметр четырехугольника.

Решение: Раз в выпуклый четырехугольник ABCD вписана окружность, то AB+CD=BC+AD. P ABCD =2(AB+CD)=2(52+53)=210

Задача 7 . Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 1:17:23 . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 84.

Решение: В выпуклый четырехугольник ABCD вписана окружность, значит AB+CD=BC+AD. По условию три стороны четырехугольника относятся как 1:17:23, пусть тогда AD=x;AB=17x; BC=23x. Итого, 24x=17x+CD; 7x=CD;

Наконец, так как по условию периметр четырехугольника равен 84, то 24x=42;

x= 7/4.Очевидно, большая сторона – это BC=23x. BC=23·(7/4) = 40,25.

Задача 8 . Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.

Решение: Сторона квадрата вдвое больше радиуса вписанной в него окружности. Поэтому сторона квадрата равна . Радиус описанной вокруг квадрата окружности равен половине его диагонали. Поэтому радиус описанной окружности есть . Ответ: 6.

Задача 9 . Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен

Решение: Шестиугольник составлен из 6 правильных треугольников. Рассмотрим правильный треугольник AOF: В нем OH = r – медиана и высота, , , тогда , АО=66 Ответ: 66.

Окружность, описанная около многоугольни к http://egemaximum.ru/zadachi-7-mnogougolnik-i-okruzhnost/

Задача 1 . Угол A четырехугольника ABCD, вписанного в окружность, равен 26˚. Найдите угол C этого четырехугольника. Ответ дайте в градусах.

Решение: Вписанный в окружность угол A опирается на дугу BCD, значит дуга BCD=52° по свойству вписанного угла. Дуга BAD, дополняющая дугу BCD до окружности, равна 360°-52°=308°. Тогда угол Cравен 308°: 2 = 154°. Ответ: 154.

Задача 2. Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 78˚, 107˚, 39˚, 136˚. Найдите угол C этого четырехугольника. Ответ дайте в градусах.

Решение: Вписанный угол C опирается на дугу BAD, равную 78˚+136˚=214˚.

Значит сам угол равен 214 : 2 = 107˚. Ответ: 107.

Задача 3 . Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB, BC, CD и AD, градусные величины которых относятся соответственно как 1:2:7:26. Найдите угол A четырехугольника ABCD. Ответ дайте в градусах.

Решение: Дуги AB,BC,CD,AD в сумме составляют 360˚. Так как градусные меры дуг AB, BC, CD и AD относятся соответственно как 1:2:7:26, то пусть AB=x, BC=2x, CD=7x,AD=26x градусов. Имеем, x+2x+7x+26x=360;36x=360;x=10. Угол A опирается на дугу BD=9x градусов, значит угол A равен 90˚: 2 = 45˚. Ответ: 45 .

Задача 4 . Четырехугольник ABCD вписан в окружность. Угол ABC равен 38˚, угол CAD равен 33˚. Найдите угол ABD. Ответ дайте в градусах.

Решение : ABC=38˚, значит дуга ADC равна 76˚. CAD=33°, значит дуга DC равна 66°. Тогда дуга AD равна 10°. Стало быть, ABD=5°. Ответ: 5 .

Задача 5 . Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 13 и .

Решение : Радиус R описанной окружности около прямоугольника – половина диагонали. По т. Пифагора: AC= ; тогда R=9. Ответ: 9.

Задача 6 . Найдите сторону квадрата, вписанного в окружность радиуса

Решение : Диагональ BD квадрата – диаметр окружности. Обозначим сторону квадрата за x. Из треугольника ABD по т. Пифагора x 2 +x 2 =( ) 2 ; 2x 2 =90 2 ·2;

x 2 =90 2 ; x=90; Ответ: 90.

Задача 7 . Меньшая сторона прямоугольника равна 16. Угол между диагоналями равен 60˚. Найдите радиус описанной окружности этого прямоугольника.

Решение : Диагонали прямоугольника – диаметры окружности.

Треугольник ABO – равносторонний, так как O=60°, AO=BO=R. Значит, R=16. Ответ: 16.

Задача 8 . Около трапеции описана окружность. Периметр трапеции равен 60, средняя линия равна 25. Найдите боковую сторону трапеции.

Решение : Раз трапеция вписана в окружность, то она равнобедренная (AB=CD).

Средняя линия трапеции l есть полусумма оснований (BC+AD)/ 2, при этом l =25. P=2AB+(BC+AD); 60=2AB+50; AB=5; Ответ: 5.

Задача 9 . Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60˚, большее основание равно 82. Найдите радиус описанной окружности этой трапеции.

Решение : 1) Трапеция, вписанная в окружность, – равнобедренная.

HQ=BC=AB=CD, AH=QD (где H,D – основания высот, опущенных к большему основанию).Из прямоугольного треугольника ABH с углом B в 30˚ AH=0,5AB по свойству катета

против угла в 30˚. Значит, AD=2AH+HQ=AB+HQ=2AB; 2AB=82; AB=41.

2) Окружность описана и вокруг треугольника ABC.Треугольник равнобедренный с углом при вершине в 120˚. Значит, BAC= BCA=30°. Применяем теорему синусов: AB/sin30° =2R, где R – радиус окружности, описанной около треугольника ABC (и около трапеции ABCD). 41/=2R; R=41; Ответ: 41.

Задача 10 . Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.

Решение : Длина высоты трапеции HQ есть сумма длин высот OQ,OH треугольников OBC и OAD.

OQ= =4 (по т. Пифагора из треугольника OQC);

OH= = 3 (по т. Пифагора из треугольника OHD);

Задача 11 . Два угла вписанного в окружность четырехугольника равны 56˚ и 99˚. Найдите больший из оставшихся углов. Ответ дайте в градусах.

Решение : Данные два угла не могут быть противоположными, так как иначе их сумма должна была бы быть 180˚ (так как они опираются на дополняющие друг друга дуги до окружности).Если A=99°, то C=180°-99°=81°. Если B=56°, то D=180°-56°=124°. Угол D и есть наибольший. Ответ: 124.

Задача 12 .Найдите радиус окружности, описанной около прямоугольника ABCD, если стороны квадратных клеток равны 1.

Решение: Диаметр описанной окружности около прямоугольника – диагональ прямоугольника. R = BD: 2=2,5. Ответ: 2,5.

Задача 13 . Периметр правильного шестиугольника равен 108. Найдите диаметр описанной окружности.

Решение: AB=BC=. =EF= P: 6 = 108 : 6 =18. Рассмотрим треугольник AOF. Он равносторонний, т.к. AO=OF=R и AOF=60°. Значит, диаметр окружности D есть 2 ·18=36. Ответ: 36.

Задача 14. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 72˚. Найдите n.

Решение: Рассмотрим треугольник AОB. Он равнобедренный, так как AO=BO=R.

Значит, A= B и AOB=180°-2 · 72°=36°.Таких равных равнобедренных треугольников у нас n штук, в сумме углы при вершине O этих треугольников дают 360˚.Тогда n=360°/=10. Ответ: 10.

Задача 15 . Около окружности, радиус которой равен ,описан правильный шестиугольник. Найдите радиус окружности, описанной около этого шестиугольника.

Решение: Треугольники AOB,BOC и т.д. – равные, равносторонние. Их сторона равна радиусу описанной около правильного шестиугольника окружности.

Из прямоугольного треугольника AOP, (где OP=R, R – радиус окружности, вписанной в правильный шестиугольник): sinA=OP/AO; , АО=3 Ответ: 3

Видео:ОПИСАННЫЕ И ВПИСАННЫЕ ОКРУЖНОСТИ ЧЕТЫРЕХУГОЛЬНИКА . §10 геометрия 8 классСкачать

По теме: методические разработки, презентации и конспекты

Рабочая программа по элективному курсу по геометрии «Решение планиметрических задач на вписанные и описанные окружности» 9 класс

Статистические данные анализа результатов проведения ЕГЭ говорят о том, что наименьший процент верных ответов традиционно дается учащимися на геометрические задачи. Задачи по планиметрии, включаемые в.

ЭЛЕКТИВНЫЙ КУРС «РЕШЕНИЕ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ НА ВПИСАННЫЕ И ОПИСАННЫЕ ОКРУЖНОСТИ» по геометрии для учащихся 9 классов

Древние греки считали окружность совершеннейшейи «самой круглой» фигурой, И в наше время в некоторыхситуациях, когда хотят дать особую оценку, используют слово «кругл.

Методическая разработка элективного курса «РЕШЕНИЕ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ НА ВПИСАННЫЕ И ОПИСАННЫЕ ОКРУЖНОСТИ» по геометрии для учащихся 9 класса

Статистические данные анализа результатов проведения ЕГЭ говорят о том, что наименьший процент верных ответов традиционно дается учащимися на геометрические задачи. Задачи по планиметрии, включаемые в.

Решение задач на вписанные и описанные многогранники

Решение задач на вписанные и описанные многогранники.

Презентация «Вписанные и описанные конусы». Решение задач

презентация по теме: «Решение задач на вписанные и описанные многогранники (пирамида)

Данная презентация позволяет организавать устную работу на уроке в 11 классе по готовым чертежам.

Презентация «Вписанная и описанная окружности четырехугольника» Геометрия 8 класс Мерзляк

Презентация «Решение задач на тему «Вписанная и описанная окружности четырехугольника» Геометрия 8 класс Мерзляк.

💡 Видео

Вписанные и описанные окружности. С. р. 3 в1 9 классСкачать

Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать

Вписанные и описанные четырехугольникиСкачать

МЕРЗЛЯК-8 ГЕОМЕТРИЯ. ОПИСАННАЯ И ВПИСАННАЯ ОКРУЖНОСТИ ЧЕТЫРЁХУГОЛЬНИКА. ПАРАГРАФ-10. ТЕОРИЯСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

8 класс Геометрия. Окружность вписанная в четырехугольник и описанная около четырехугольника Урок #4Скачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

3 правила для вписанного четырехугольника #shortsСкачать

ср4 Вписанные и описанные четырехугольники. 2 вариант, 9 классСкачать

Тема 9. Вписанные и описанные четырехугольникиСкачать

Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать