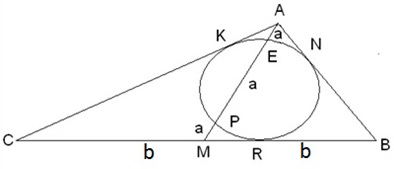
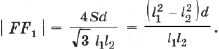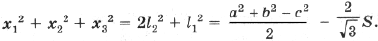Окружность, вписанная в треугольник ABC, делит медиану AM на три части. Определите, как сторона BC относится к стороне AB и к стороне CA.
Решение:
(№679 Математика 11, Л.А. Латотин, Б.Д. Чеботаревский)
Поскольку квадрат отрезка касательной равен произведению секущей на ее внешнюю часть, то AK 2 = 2a·a= 2a 2 .
Используем формулу для медианы треугольника:
Последнее равенство разделим на 4·a ≠ 0, получим: 5·a = 2·(2) 1/2 ·b, откуда a = (2·(2) 1/2 ·b)/5.
Выразив все стороны треугольника через b, получим следующее:
=
- Окружность делит медиану на три части
- Окружность, вписанная в треугольник делит медиану на три части
- Медиана треугольника
- Некоторые малоизвестные факты из геометрии треугольника
- Одна из медиан треугольника делится вписанной окружностью на три равные части?
- Вершины правильного треугольника делят окружность на 3 дуги?
- Площадь треугольника равна 84, одна из его сторон 13, а радиус вписанной окружности равен 4?
- В треугольнике ABC сторона AB на 4 больше стороны BC?
- Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 1, считая от вершины, проттиволежищей основанию?
- В треугольник, стороны которого равны 8, 13 и 15 вписана окружность?
- Около правильного треугольника АВС описана окружность, Длина дуги АВ равна 2П см?
- Площадь треугольника равна 84, одна из его сторона равна 13, а радиус вписанной окружности равен 4?
- Медиана, проведенная к одной из боковых сторон равнобедренного треугольника, делит его периметр на две части длинной 15 и 6?
- Точка касания окружности, вписанной в треугольник, делит одно из его сторон на отрезки 12 и 14?
- Радиус окружности вписанной в прямоугольный треугольник равен 5см, а длина одного из катетов равна 12см?
- 🎥 Видео
Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Окружность делит медиану на три части
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Окружность, вписанная в треугольник делит медиану на три части
Окружность, вписанная в треугольник ABC, делит медиану AM на три части. Определите, как сторона BC относится к стороне AB и к стороне CA.
Решение:
(№679 Математика 11, Л.А. Латотин, Б.Д. Чеботаревский)
Поскольку квадрат отрезка касательной равен произведению секущей на ее внешнюю часть, то AK 2 = 2a·a= 2a 2 .
Используем формулу для медианы треугольника:
Последнее равенство разделим на 4·a ≠ 0, получим: 5·a = 2·(2) 1/2 ·b, откуда a = (2·(2) 1/2 ·b)/5.
Выразив все стороны треугольника через b, получим следующее:
=
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Медиана треугольника
Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).
Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.
На рисунке 1 медианой является отрезок BD .
Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).
Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),
и заметим, что (см. раздел нашего справочника «Площадь треугольника»)
Поскольку отрезок BD является медианой, то
что и требовалось доказать.
Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.
Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).
Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).
Теперь рассмотрим четырёхугольник FEDG (рис. 5).
Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,
Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,
Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.
Следствие . Все три медианы треугольника пересекаются в одной точке.
Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).
Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.
Определение . Точку пересечения медиан треугольника называют центроидом треугольника.
Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).
Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна 
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

 Некоторые малоизвестные факты из геометрии треугольника
Некоторые малоизвестные факты из геометрии треугольника
Статья представляет собой дополнение к очень популярной теме «Геометрия треугольника». В ней рассматриваются некоторые известные факты с оригинальными авторскими доказательствами. Некоторые пункты можно разобрать дополнительно к отдельным темам: вписанная окружность, теорема Пифагора, векторный метод, точка Ферма, треугольники Наполеона. В конце каждого пункта приводятся упражнения, позволяющие закрепить рассматриваемые темы, уяснить их с разных сторон. Во многих случаях сами упражнения содержат важный теоретический материал. Многие упражнения взяты из известных учебников.
1. Симметричный вывод формулы Герона
Точки касания вписанной окружности со сторонами треугольника обозначим через A1, B1, C1 (рис. 1). Треугольники AIB1 и AIC1, BIA1 и BIC1, CIA1 и CIB1 попарно равны, как прямоугольные треугольники, имеющие общую гипотенузу и равные углы.
откуда AB1 = AC1 = 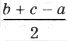
Аналогично CA1 = CB1 =
и BA1 = BC1 = 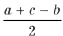
Обозначим углы Р C1IB1 = a , Р C1IA1 = b , Р A1IB1 = g . В D AIB1 катеты связаны соотношением
откуда
.
Аналогично
.
Так как
,
то легко доказать
(*)
Подставив в (*) выражения
через a, b, c и r, получим
= ,
откуда
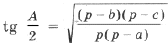
Здесь и далее через R обозначен радиус описанной окружности.
3. Докажите, что в D ABC биссектриса угла A, средняя линия, параллельная AC, и прямая, соединяющая точки касания вписанной окружности со сторонами CB и CA, пересекаются в одной точке.
4. Докажите, что сумма квадратов расстояний от точек касания вписанной в треугольник окружности с его сторонами до центра описанной равна 3R 2 – 4Rr – r 2 .
5. Центр окружности, вписанной в прямоугольный треугольник, находится на расстоянии и см от концов гипотенузы. Найдите катеты этого треугольника.
6. В D ABC известно BC = a, Р A = a , Р B = b . Найдите радиус окружности, пересекающей все его стороны и высекающей на каждой из них хорды длины d.
7. В D ABC проведена медиана AM. Может ли радиус окружности, вписанной в D ABM, быть ровно в два раза больше радиуса окружности, вписанной в D ACM?
8*. Окружность, вписанная в D ABC, делит медиану BM на три равные части. Найдите отношение BC : CA : AB.
2. К теореме Пифагора
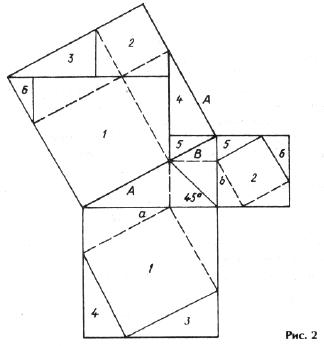
Многие доказательства теоремы Пифагора используют характерный рисунок квадратов, построенных во внешнюю стороны на сторонах треугольника («Пифагоровы штаны»).
Доказательство сводится к доказательству формулы
где S – площадь квадрата, построенного на гипотенузе, S1, S2 – площади квадратов, построенных на катетах.
Обычно при этом используется разбиение квадратов на равные части, совмещающиеся друг с другом.
Минимальное число фигур разбиения – 5 (Ан-Нариций, древнеиндийское «колесо с лопастями»), бывает 7 и 8). На рис. 2 показано разбиение, в котором совмещается 6 фигур.
Биссектриса прямого угла исходного треугольника делит гипотенузу на части длиной A и B, причем по свойству биссектрисы A : B = a : b, где a и b – длины катетов.
Проведем в квадрате, построенном на гипотенузе, штриховые линии на расстоянии A и B от сторон. Рассмотрим выделенный жирным контуром прямоугольный треугольник. Он подобен исходному, так как его катеты A и B пропорциональны a и b. Поэтому гипотенуза выделенного треугольника параллельна катету b, так как соответствующие накрест лежащие углы равны. Теперь можно провести остальные линии разбиения: в квадрате, построенном на гипотенузе, – параллельно катетам, а в квадратах, построенных на катетах, – параллельно сторонам квадрата, построенного на гипотенузе (причем во втором случае длины отрезков разбиения равны A и B). Нетрудно видеть, что при этом получаются совмещающиеся фигуры.
1. Высота, опущенная на гипотенузу, делит прямоугольный треугольник на два, подобных исходному. Пользуясь тем, что площади подобных фигур относятся как квадраты их линейных элементов, докажите теорему Пифагора (Ч. Тригг).
2. Впишем в прямоугольный треугольник окружность, которая точками касания делит катеты на отрезки, два из которых по длине совпадают с r – радиусом окружности. Пользуясь результатами п. 1, еще раз докажите теорему Пифагора (доказательство Мёльманна).
3. Точки O1, O2, O3 – соответственно центры квадратов, построенных на катете и гипотенузе, C – вершина прямого угла исходного треугольника. Докажите, что отрезки O1O2 и O3C перпендикулярны, а их длины равны.
4. Найдите площадь O1O2O3 (см. упражнение 3), если длины катетов прямоугольного треугольника равны a и b.
3. Теорема Лейбница
Если O – точка пересечения медиан D ABC, P – произвольная точка плоскости, то (рис. 3)
Доказательство. Возведем векторное равенство
Аналогично получаются равенства:
Складывая эти три равенства, получаем
так как сумма векторов в скобках равна нулю. Отсюда
Так как
то отсюда следует доказываемая формула.
Дополнительное упражнение. Получите формулы для медиан треугольника
1. Докажите, что сумма квадратов расстояний от произвольной точки плоскости до вершины треугольника является минимальной, если точка совпадает с точкой пересечения медиан.
2. Вычислите расстояние от точки пересечения медиан до центра описанной окружности.
3. Вычислите расстояние от точки пересечения медиан до центра вписанной окружности.
4. Докажите, что для произвольной точки P, лежащей на окружности, вписанной в равносторонний D ABC,
PA 2 + PB 2 + PC 2 = const.
5. Полупериметр D ABC равен p. Докажите, что для любой точки M плоскости имеет место неравенство
причем равенство достигается лишь в случае, когда ABC – правильный треугольник и M – его центр.
6*. Радиус круга, описанного около треугольника, равен R. Расстояние от центра этого круга до точки пересечения медиан треугольника равно d. Найдите произведение площади данного треугольника и треугольника, образованного прямыми, проходящими через его вершины перпендикулярно медианам, из этих вершин выходящим. Указание. Если O – точка пересечения медиан исходного D ABC, то отрезки OA, OB, OC делят второй больший треугольник на 3 вписанных четырехугольника, площади которых можно выразить через стороны и площади треугольников AOB, AOC, BOC, а, значит, – ABC.
7*. Пусть ABC – правильный треугольник со стороной a, M – некоторая точка плоскости, находящаяся на расстоянии d от центра треугольника ABC. Докажите, что площадь треугольника, стороны которого равны отрезкам MA, MB и MC, выражается формулой
Точкой Ферма называется такая точка треугольника, сумма расстояний от которой до вершин треугольника является минимальной. Когда все углы треугольника меньше 120°, то точка Ферма – это такая точка F в треугольнике, из которой все стороны треугольника видны под одним и тем же углом 120°.
Доказательство. Проведем через вершины исходного D ABC прямые, перпендикулярные отрезкам AF, BF и CF соответственно. Они пересекутся в вершинах некоторого правильного треугольника A1B1C1. Для любой точки P D A1B1C1 сумма длин перпендикуляров, опущенных из P на стороны этого треугольника, есть постоянное число (в частности, оно равно AF + BF + CF), так как она равна , где S – площадь A1B1C1, a – его сторона. Очевидно, что PA не меньше длины перпендикуляра, опущенного из P на сторону B1C1, проходящую через A. Тем более, PA + PB + PC не меньше суммы длин всех перпендикуляров, которая равна AF + BF + CF, и равенство достигается, когда P совпадает с F.
Иногда точку Ферма называют точкой Торичелли или точкой Брокара.
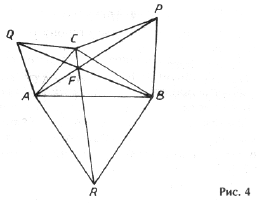
Чтобы построить точку Ферма, надо на сторонах D ABC во внешнюю сторону построить равносторонние треугольники ABR, BCP и ACQ. Отрезки AP, BQ и CR пересекаются в точке F – точке Ферма (рис. 4).
Действительно, пусть AP и BQ пересекаются в точке F. При повороте вокруг точки C на 60° D CQB переходит в D CAP. Следовательно, угол между QB и AP Р QFA = 60°, и точка F лежит на окружности, описанной около D AQC. Аналогично угол Р PFB = 60°, и точка F лежит на окружности, описанной около D BPC. Так как угол Р AFB = 120°, то точка F лежит на окружности, описанной около D ABR, значит, Р AFR = 60°. Так как при повороте на 60° вокруг точки B D APB переходит в D RCB, то угол между AP и CR равен 60° и точка F лежит на CR.
1. Используя теорему Птолемея для четырехугольника AFBR и обозначив расстояния от F до вершин D ABC через x1, x2, x3, найдите AP = BQ = CR (рис. 4).
5. Треугольники Наполеона
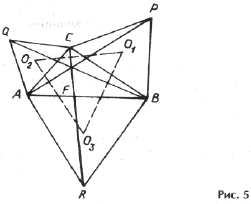
Если на сторонах D ABC внешним образом построить равносторонние треугольники, то их центры являются вершинами равностороннего внешнего треугольника Наполеона.
Действительно, вершины D O1O2O3 являются центрами окружностей, описанных вокруг равносторонних треугольников и пересекающихся в точке F. Поэтому стороны D O1O2O3 перпендикулярны отрезкам FA, FB и FC, и углы между ними равны 60° (рис. 5).
Если на сторонах D ABC построить равносторонние треугольники во внутреннюю сторону и соединить их центры, то получится равносторонний внутренний треугольник Наполеона.
Применив теорему косинусов к D CO1O2, можно вывести формулу для стороны внешнего треугольника Наполеона:
где S – площадь D ABC.
Для стороны внутреннего треугольника Наполеона аналогично получается
1. Докажите, что центры треугольников Наполеона совпадают с точкой пересечения медиан (для этого вычислите расстояние от какой-нибудь вершины треугольника Наполеона до точки пересечения медиан и покажите, что оно на зависит от рассматриваемой величины и равно
где l – длина стороны треугольника Наполеона).
2. Докажите, что разность площадей треугольников Наполеона (внешнего и внутреннего) равна площади D ABC.
3. Докажите, что
4. Применив теорему Лейбница для внешнего треугольника Наполеона и точки Ферма F, вычислите расстояние от точки пересечения медиан, которая является центром треугольника Наполеона, до точки Ферма.
5. Докажите, что
6. Докажите, что PQ 2 + QR 2 + RP 2 = a 2 + b 2 + c 2 + 9l1 2 .
7. Докажите, что точка пересечения медиан D PQR совпадает с точкой G пересечения медиан D ABC.
Указание. Вычислите длины PG, QG, RG и примените теорему Лейбница; второй способ – докажите, что векторная сумма
8. На сторонах треугольника во внешнюю сторону построены квадраты. Докажите, что точка пересечения медиан треугольника с вершинами в центрах этих квадратов совпадает с точкой пересечения медиан данного треугольника.
(См. указание к упр. 7, второй способ.)
9. Рассмотрим центроиды A1, B1, C1 треугольников AQR, BPR и CQP соответственно. Докажите, что D A1B1C1 – правильный и центр его совпадает с центроидом G данного D ABC.
Указание. Докажите, что равны векторы
10. Докажите, что треугольники A1B1C1 и O1O2O3 симметричны относительно их общего центра G и поэтому шестиугольник O1C1O2A1O3B1 – правильный и его центр совпадает с центроидом G данного треугольника. Сторона этого шестиугольника
.
11. Докажите, что середины A2, B2, C2 отрезков AO1, BO2, CO3 являются вершинами еще одного равностороннего треугольника он гомотетичен внутреннему треугольнику Наполеона с 
12*. Пусть A3, B3, C3 – середины отрезков QR, PR и QP соответственно. Докажите, что прямые AA3, BB3, CC3 пересекаются в одной точке или параллельны.
13. Докажите, что если подобные треугольники PCB, CQA, BAR построены извне на сторонах произвольного D ABC, то окружности, описанные вокруг этих трех треугольников, имеют общую точку.
14. Докажите, что в условиях упражнения 13 центры трех указанных окружностей образуют треугольник, подобный треугольникам PCB, CQA, BAR.
15. Докажите, что если на двух сторонах треугольника построены квадраты, то окружности, описанные вокруг них, пересекаются на окружности, построенной на третьей стороне, как на диаметре, и центры этих трех окружностей являются вершинами равнобедренного прямоугольного треугольника.
16. Докажите, что прямые AO1, BO2, CO3 пересекаются в одной точке (см. рис. 5).
Указание. Продолжить эти прямые до пересечения со сторонами треугольника ABC и применить теорему Чевы.
6. Расстояние от точки Ферма до центра описанной окружности
Ранее было получено, что
где
l1 – длина стороны внешнего треугольника Наполеона (упражнения 4.1, 4.2 и 5.5).
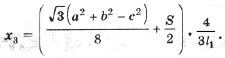
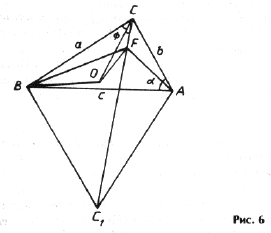
Точка Ферма F лежит на прямой CC1, которая соединяет вершину C исходного D ABC с вершиной C1 равностороннего D ABC1 (рис. 6); O – центр описанной окружности.
Обозначим угол BCC1 через j ;

С учетом этого преобразуем формулу (2):
Найдем по теореме косинусов для D BCC1
Для a (применим теоремы косинусов и синусов к D ABC)
Подставив полученные выражения в (3), находим
Тогда с учетом (1) получим
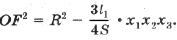
(5)
которую преобразуем к виду
(6)
где d – расстояние от точки пересечения медиан до центра описанной окружности.
Дополнение: точка F1 пересечения прямых AP ‘, BO ‘ и CR ‘, где ABR ‘, BCP ‘ и ACO ‘ – равносторонние треугольники, построенные на сторонах D ABC во внутреннюю сторону, является точкой, двойственной точке Ферма. Точка F1 лежит на окружности, описанной около внешнего треугольника Наполеона. Расстояние между точками F и F1 равно (без доказательства)
1. Докажите, что расстояние от точки Ферма F до центра описанной окружности O больше расстояния от точки пересечения медиан G до центра описанной окружности O.
2. Вычислите угол Р OGF в обозначениях упражнения 1 и формулы (6).
3. Доказать, что
4*. Точка F – точка Ферма D ABC (углы которого меньше 120°). Докажите, что прямые Эйлера треугольников AFB, BFC и CFA пересекаются в одной точке.
Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Одна из медиан треугольника делится вписанной окружностью на три равные части?
Геометрия | 10 — 11 классы
Одна из медиан треугольника делится вписанной окружностью на три равные части.
Покажи — те, что одна из сторон треугольника вдвое длиннее другой.
Решение прицеплено в картинке.
Видео:ЗАДАЧА - ЧУМА!Скачать

Вершины правильного треугольника делят окружность на 3 дуги?
Вершины правильного треугольника делят окружность на 3 дуги.
Найдите длину одной из этих дуг, если сторона правильного треугольника равно 2√3.
Видео:8. Медиана треугольника и её свойства.Скачать

Площадь треугольника равна 84, одна из его сторон 13, а радиус вписанной окружности равен 4?
Площадь треугольника равна 84, одна из его сторон 13, а радиус вписанной окружности равен 4.
Найти сумму длин двух других сторон треугольника.
Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

В треугольнике ABC сторона AB на 4 больше стороны BC?
В треугольнике ABC сторона AB на 4 больше стороны BC.
Медиана BE делит треугольники на два треугольника .
В каждый из этих треугольников вписана окружность Найдите расстояние между точками касания окружностей с медианой BE .
Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 1, считая от вершины, проттиволежищей основанию?
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 1, считая от вершины, проттиволежищей основанию.
Найдите периметр треугольника.
Видео:ЕГЭ 2024 по математике. №1,17 Медиана, биссектриса, высота, серединный перпендикулярСкачать

В треугольник, стороны которого равны 8, 13 и 15 вписана окружность?
В треугольник, стороны которого равны 8, 13 и 15 вписана окружность.
Найдите длины отрезков этих сторон, на которые они делятся точками касания с вписанной окружностью.
Видео:Все факты о медиане треугольника для ЕГЭСкачать

Около правильного треугольника АВС описана окружность, Длина дуги АВ равна 2П см?
Около правильного треугольника АВС описана окружность, Длина дуги АВ равна 2П см.
Найдите длину одной из медиан треугольника АВС.
Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Площадь треугольника равна 84, одна из его сторона равна 13, а радиус вписанной окружности равен 4?
Площадь треугольника равна 84, одна из его сторона равна 13, а радиус вписанной окружности равен 4.
Найдите две другие стороны треугольника.
Видео:Вписанная окружность. ЗАДАЧА ИЗ ГОНКОНГА!Скачать

Медиана, проведенная к одной из боковых сторон равнобедренного треугольника, делит его периметр на две части длинной 15 и 6?
Медиана, проведенная к одной из боковых сторон равнобедренного треугольника, делит его периметр на две части длинной 15 и 6.
Найти длины сторон треугольника.
Видео:✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

Точка касания окружности, вписанной в треугольник, делит одно из его сторон на отрезки 12 и 14?
Точка касания окружности, вписанной в треугольник, делит одно из его сторон на отрезки 12 и 14.
Найдите радиус этой окружности, если периметр треугольника = 84.
Видео:ОПИСАННАЯ и ВПИСАННАЯ окружности. §21 геометрия 7 классСкачать

Радиус окружности вписанной в прямоугольный треугольник равен 5см, а длина одного из катетов равна 12см?
Радиус окружности вписанной в прямоугольный треугольник равен 5см, а длина одного из катетов равна 12см.
Найти P треугольника.
Если вам необходимо получить ответ на вопрос Одна из медиан треугольника делится вписанной окружностью на три равные части?, относящийся к уровню подготовки учащихся 10 — 11 классов, вы открыли нужную страницу. В категории Геометрия вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.
30 : 5 = 6 см отрезок МЕ. Так значит ДМ = 24 см.
Скрещивающиеся прямые не имеют общих точек. У прямых AD и AB — общая точка A. У прямых AD и BD — общая точка D. У прямых AD и CD — общая точка D. ПрямыеAD и BC — скрещивающиеся.
BD — медиана и высота значит треугольник ABC равнобедренный, AB = BC, AD = DC, AB + AD = PABD — BD = 15 — 4 = 11 см PABC = 2 * (AB + AD) = 11 * 2 = 22 см периметр треугольника ABC = 22 cм.
ВС = АВ + АС Х = 6 + 9 = 15 ВС = 15.
Т. к точка А делит отрезок ВС на два отрезка, то этот отрезок ВС равен сумме двух получившихся отрезков, т. Е ВС = АВ + АС = 6 + 9 = 15. Ответ : отрезок ВС равен 15 сантиметрах.
Если О — центр окружности, то радиус окружности = 5. И АD = 5.
Подлежащие — одна черта, Сказуемое — две черты обстоятельство — точка пунктир Дополнение — пунктир.
Подлежащее одной чертой, сказуемое двумя, обстоятельство : _. _. _. В общем обстоятельство точка — тире, а дополнение пунктирной линией : — — — -.
Решение задачи во вложенном файле.
В прямоугольном ∆ АВС∠С = 90°, высота СК делит гипотенузу на отрезки АВ = 5 см, кВ = 1 см. Определите длину высоты СК. Высотапрямоугольноготреугольника, проведеннаяк гипотенузе, естьсреднеегеометрическое (среднеепропорциональное) между отрезками, н..
🎥 Видео
Найдите площадь треугольника, если его медианы равны 3, 4 и 5Скачать
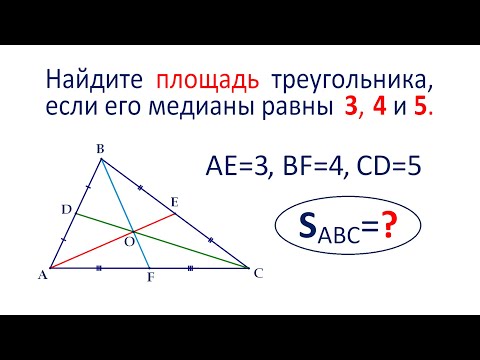
Окружность вписана в равносторонний треугольник, найти радиусСкачать

Геометрия, ЕГЭ, часть 2. Задача 3. Все свойства медианы + формула для её нахожденияСкачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Тема 8. Прямоугольный треугольник и его описанная и вписанная окружностиСкачать














 Некоторые малоизвестные факты из геометрии треугольника
Некоторые малоизвестные факты из геометрии треугольника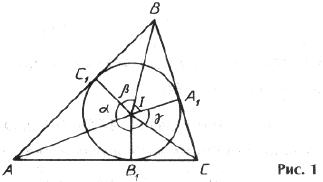
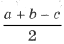
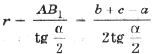
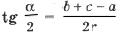 .
.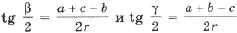 .
.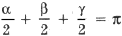 ,
,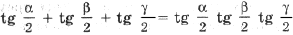 (*)
(*)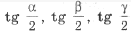
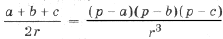 = ,
= ,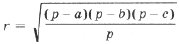
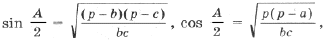
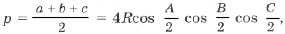
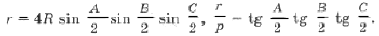
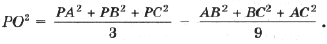

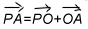
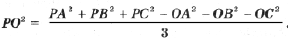
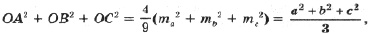
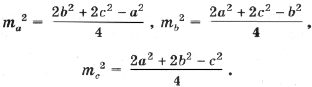
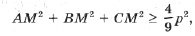
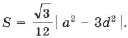
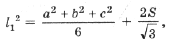
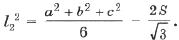
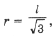
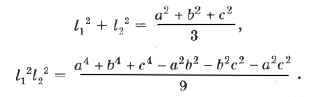
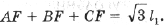
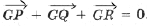
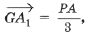
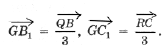
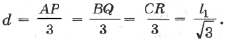 .
.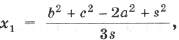
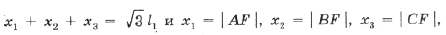

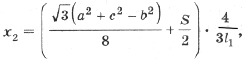
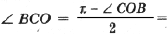
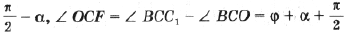
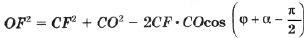
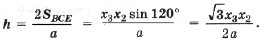
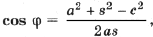
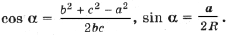
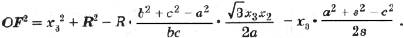
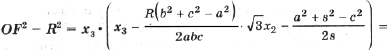
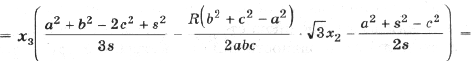
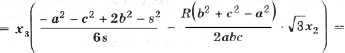
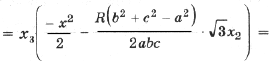
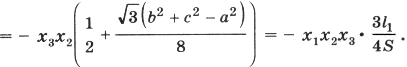
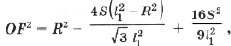 (5)
(5)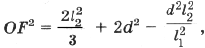 (6)
(6)