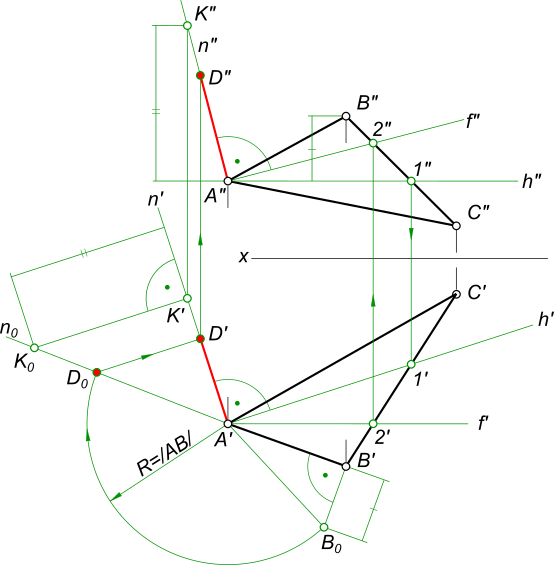
Восстановить перпендикуляр плоскости треугольника (5 видео)

Восстановить перпендикуляр к плоскости

Без применения способов преобразования чертежа через точку A восстановить перпендикуляр AD к плоскости Σ(ABC), если /AD/ = /AB/

Содержание

Комментарии
Решения задачи
Комментарии
Инженерная графика. Последовательность решения задач. Размеры и заполнение надписи. Расположение форматов
Страницы работы
Фрагмент текста работы
Консультации по дипломным работам
Рассмотрим примеры.
🎥 Видео

Решения задачи

Для решения задачи необходимо использовать признаки перпендикулярности прямой к плоскости и способ прямоугольного треугольника.

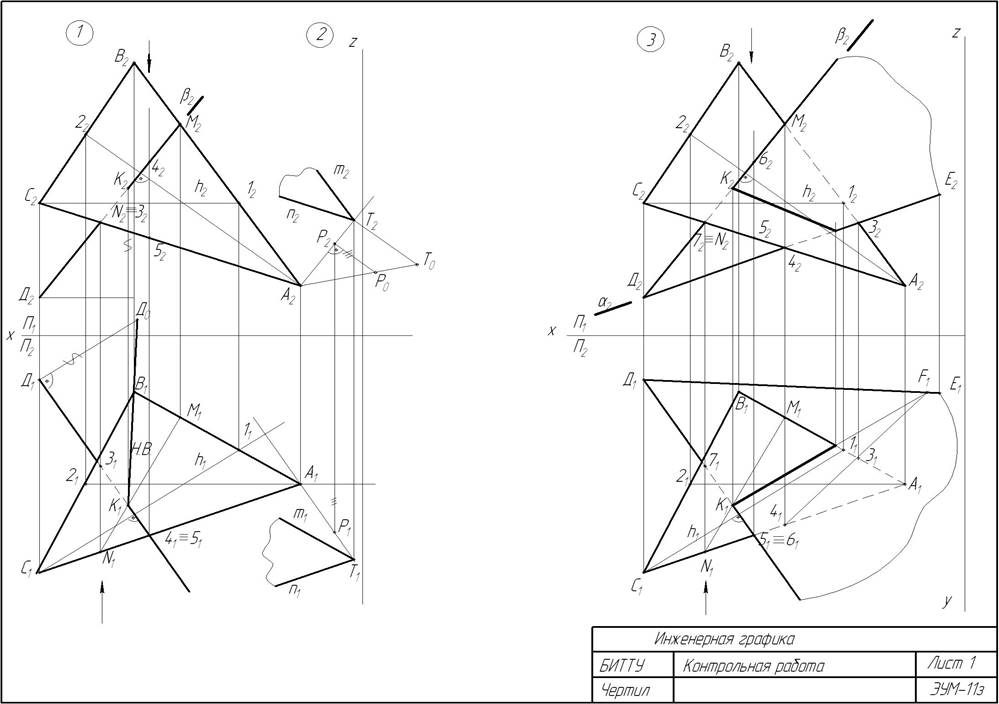
Инженерная графика. Последовательность решения задач. Размеры и заполнение надписи. Расположение форматов

Страницы работы

Фрагмент текста работы

Проекции прямых, контуры плоскостей, поверхностей обвести сплошной толстой линией S=1мм., а все вспомогательные линии, оси – сплошной тонкой линией по ГОСТ 2.303 – 68. Все вспомогательные построения не стирать и все точки на чертеже обозначить. Надписи и обозначения в виде букв и цифр выполняют шрифтом размером 3,5 и 5 по ГОСТ 2.304-81.

На экзамене студенту предлагается решить две задачи и ответить на один теоретический вопрос. Решение задач выполняется на листе чертёжной бумаге (ватман) формата А3 (297х420) с помощью чертёжных инструментов в карандаше. На экзамен принести с собой лист ватмана , два треугольника, карандаши, циркуль, резинку.

СОДЕРЖАНИЕ КОНТРОЛЬНОЙ РАБОТЫ

На листе 1 выполнить задачи 1,2,3.

Пример выполнения листа на рис.3 .Задачи 1 и 2 совместить на одном чертеже в левой части листа, а задачу 3 расположить в правой части. Точку Е строить только для задачи 3.

Задача 1. Определить расстояние от точки Д до плоскости заданной треугольником АВС. Определить видимость перпендикуляра, проходящего через точку Д и плоскость треугольника АВС.

Данные для выполнения задачи взять из табл.1, в соответствии с вариантом.

Указания к решению задачи 1

Если прямая перпендикулярна к плоскости, то её проекции перпендикулярны к одноимённым проекциям одноимённых линий уровня (горизонтали — h и фронтали –f) этой плоскости.

Задачу выполнить в следующей последовательности:

1) в плоскости треугольника АВС провести горизонталь – h и фронталь – f; 2) из точки Д₁ опустить перпендикуляр к горизонтальной проекции горизонтали-h₁, а из точки Д₂ опустить перпендикуляр к фронтальной проекции фронтали-f₂;.

Рис.3. Пример выполнения задач 1,2,3. Лист 1

3) определить точку пересечения перпендикуляра с плоскостью АВС, для чего перпендикуляр заключить в проецирующую плоскость , найти линию пересечения вспомогательной плоскости и плоскости АВС и отметить точку К, в которой эта линия пересекается с перпендикуляром;

4) определить натуральную величину (Н.В.) расстояния от точки Д до плоскости треугольника АВС (прямая ДК), применяя способ прямоугольного треугольника;

5) определить видимость проекции перпендикуляра методом конкурирующих точек.

Задача 2. Построить плоскость, параллельную заданной плоскости АВС и отстоящую от неё на расстоянии 45 мм.

Данные для выполнения задачи взять из табл.1.

Указания к решению задачи 2.

Две плоскости параллельны, если две пересекающие прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости.

Задачу выполнить в следующей последовательности:

1) в плоскости АВС выбрать произвольную точку (на рис.2 взята точка А) и из неё восстановить перпендикуляр к плоскости АВС;

2) на перпендикуляре отметить произвольную точку Р;

3) определить методом прямоугольного треугольника натуральную величину отрезка АР;

4) на натуральной величине произвольного отрезка перпендикуляра найти точку Т, расположенную на расстоянии 45мм. от плоскости, и построить проекции этой точки на проекциях перпендикуляра;

5) через точку Т провести искомую плоскость, соблюдая условия параллельности плоскостей.

Задача 3. Через прямую ДЕ провести плоскость, перпендикулярную плоскости треугольника АВС. Определить видимость плоскостей. Данные для выполнения задачи взять из табл.1.

Данные значений координат точек для решения задач 1,2,3. Лист 1

Видео:5. Начертательная геометрия. Практикум. Перпендикуляр к плоскостиСкачать

Консультации по дипломным работам

Видео:Теорема о трех перпендикулярах. Признак перпендикулярности плоскостей | Математика | TutorOnlineСкачать

Рассмотрим примеры.

1. В точке А восстановить перпендикуляр m к плоскости Σ(ΔАВС).

Сначала через вершину А плоскости Σ проведём горизонталь h и фронталь f (рис.5.8). Горизонтальную проекцию искомого перпендикуляра n1 необходимо провести перпендикулярно к горизонтальной проекции горизонтали плоскости, а фронтальную проекцию перпендикуляра n2 – перпендикулярно к фронтальной проекции фронтали плоскости.

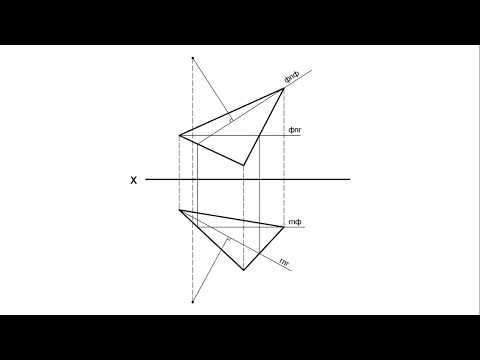
2. Через точку А провести плоскость, перпеникулярную прямой m.

Искомую плоскость зададим двумя пересекающимися прямыми – горизонталью и фронталью, каждая из которых должна быть перпендикулярна к прямой m (рис.5.9). Поэтому горизонтальная проекция горизонтали h1 должна проходить через горизонтальную проекцию А1 точки А перпендикулярно горизонтальной проекции прямой m1. Фронтальная проекция горизонтали h2 проходит через фронтальную проекцию А2 точки А, параллельно оси x12. У фронтали наоборот – фронтальная проекции f2, проходящая через фронтальную проекцию А2 точки А, перпендикулярна фронтальной проекции прямой m2, а горизонтальная проекции f1 проходит через точку А1 параллельно оси x12. Стоимость крыши из металлочерепицы: черепица.

4. Взаимно-параллельные плоскости

Для параллельных плоскостей справедливо следующее утверждение: если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, эти плоскости параллельны друг другу.

Поэтому для построения плоскости, параллельной некоторой плоскости, необходимо в заданной плоскости взять две произвольные пересекающиеся прямые и задать искомую плоскость двумя прямыми соответственно параллельными выбранным прямым. Рассмотрим пример.

Через точку A провести плоскость, параллельную плоскости Θ(a||b) (рис.5.10).

Так как плоскость Θ задана двумя параллельными прямыми необходимо провести в ней вспомогательную прямую 12, пересекающуюся с прямыми a и b. Затем через заданную точку А нужно провести прямую m, параллельную прямой a, и прямую n, параллельную прямой 12. Тогда прямые m и n будут определять искомую плоскость, параллельную заданной плоскости Θ.

Иногда бывает нужно определить, параллельны ли друг другу две заданные плоскости. Для ответа на этот вопрос необходимо в одной из плоскостей провести две пересекающиеся прямые и попытаться построить в другой плоскости две прямые соответственно параллельные построенным прямым. Если такие прямые построить можно, значит, плоскости параллельны, если нельзя – не параллельны.

5. Взаимно-перпендикулярные плоскости

Известно, что две плоскости взаимно перпендикулярны, если каждая из них проходит через перпендикуляр к другой плоскости или перпендикулярно к прямой, лежащей в другой плоскости. Отсюда следуют два способа построения плоскости, перпендикулярной к другой плоскости:

1) плоскость проводят через прямую, перпендикулярную к заданной плоскости;

2) плоскость проводят перпендикулярно прямой, лежащей в заданной плоскости.

Таким образом, построение взаимно перпендикулярных плоскостей сводится к построению взаимно перпендикулярных прямой и плоскости. Рассмотрим пример.

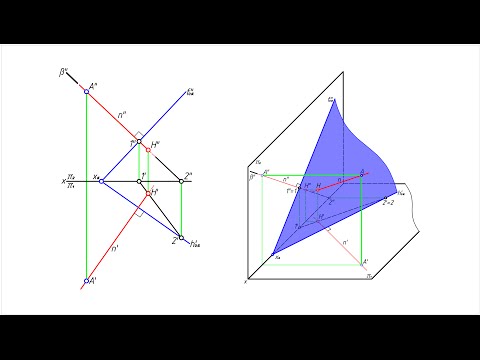
Через точку D провести плоскость, перпендикулярную к плоскости Σ (ΔАВС) (рис.5.11).

Сначала строим в заданной плоскости прямые уровня – горизонталь h и фронталь f. Искомая плоскость должна содержать перпендикуляр к плоскости Σ. Поэтому через точку D1 проводим горизонтальную проекцию перпендикуляра m1 перпендикулярно горизонтальной проекции h1 горизонтали. Фронтальная проекция m2 перпендикуляра проводится через точку D2 перпендикулярно фронтальной проекции фронтали f2. Для задания искомой плоскости необходимо провести через точку D произвольную прямую n (так как ни каких других условий больше не задано).