Вопросы по теме окружность геометрия

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Определение окружности

• Отрезки в окружности

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Определение окружности

Окружность – геометрическое место точек, равноудаленных от данной точки.

Эта точка называется центром окружности .

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Отрезки в окружности

Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.

Хорда a – отрезок, соединяющий две точки на окружности.

Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).

O A – радиус, D E – хорда, B C – диаметр.

Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.

Касательная к окружности – прямая, имеющая с окружностью одну общую точку.

Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.

Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).

Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.

Видео:Окружность. 7 класс.Скачать

Дуга в окружности

Часть окружности, заключенная между двумя точками, называется дугой окружности .

Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .

Теорема 4:
Равные хорды стягивают равные дуги.

Если A B = C D , то ∪ A B = ∪ C D

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Углы в окружности

В окружности существует два типа углов: центральные и вписанные.

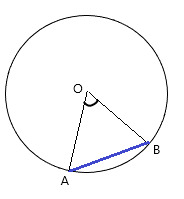
Центральный угол – угол, вершина которого лежит в центре окружности.

∠ A O B – центральный.

Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α

Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.

Градусная мара всей окружности равна 360 ° .

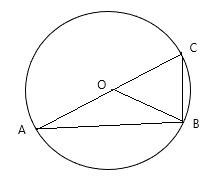
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.

∠ A C B – вписанный.

Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α

Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .

∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2

Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .

∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Длина окружности, длина дуги

Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .

Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .

Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.

Длина окружности находится по формуле:

Длина дуги окружности , на которую опирается центральный угол α равна:

l α = π R 180 ∘ ⋅ α

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Площадь круга и его частей

Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.

Круг – часть пространства, которая находится внутри окружности.

Иными словами, окружность – это граница, а круг – это то, что внутри.

Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.

Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.

Площадь круга находится по формуле: S = π R 2

Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Примеры сектора в реальной жизни: кусок пиццы, веер.

Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α

Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.

Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.

Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.

S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α

Видео:7 класс, 21 урок, ОкружностьСкачать

Теорема синусов

Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.

Видео:Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с окружностями.

Видео:Окружность и круг, 6 классСкачать

Вопросы по теме окружность геометрия

Тесты по геометрии 7 класс. Тема: «Окружность»

Правильный вариант ответа отмечен знаком +

1. Радиусом окружности называется отрезок … Закончите определение:

— соединяющий две любые точки окружности

+ соединяющий центр окружности с какой-либо точкой окружности

— пересекающий окружность в двух точках

— ограничивающий дугу окружности

2. Окружность – это совокупность … точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки O, которая называется центром окружности. Вставьте пропущенное слово:

3. Часть плоскости, ограниченной окружностью, называется:

4. Центр окружности – это:

— точка, делящая радиус пополам

+ точка, равноудаленная от всех точек окружности

— точка, которая находится в пределах окружности

— точка, расположенная на диаметре окружности

5. Отрезок, проходящий через две точки и центр окружности, называется:

6. Как называется прямая, имеющая одну общую точку с окружностью?

7. Какой отрезок называется хордой?

+ соединяющий 2 точки окружности

— равный двум радиусам

— разделяющий окружность на 2 равные дуги

8. Дуга окружности – это:

+ часть окружности, ограниченная хордой

— множество равноудаленных от центра окружности точек

— две точки, соединенные отрезком

— часть окружности, равная радиусу

9. Диаметр, перпендикулярный хорде… Закончите утверждение:

+ делит эту хорду и дуги, которые она стягивает, пополам

— делится хордой пополам

— равен произведению длины радиуса и хорды

— называется секущей окружности

тест 10. Если 2 хорды равны, следовательно, они… Закончите утверждение:

— проходят через центр окружности

— выходят из одной точки окружности

— пересекают друг друга

+ стягивают 2 одинаковые дуги

11. Укажите формулу диаметра окружности D:

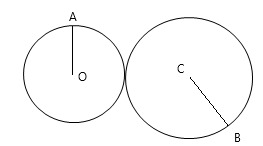
12. Две окружности пересекаются в одной точке. Радиус OA=20 см, радиус CB=30 см. Найдите расстояние между двумя центрами окружностей.

13. Дана окружность с центром O, в которую вписан треугольник ABC. Медиана треугольника OB=8 см. Чему равен диаметр окружности?

14. Дана окружность с центром О. Угол AOB=60 о , радиус OB=10 см. Найдите хорду AB.

15. Через три точки, которые не лежат на одной прямой… Закончите утверждение:

— можно провести три различных окружности

— можно провести равносторонний треугольник

+ можно провести только одну окружность

— нельзя построить параллельные прямые

16. Если две окружности соприкасаются в одной точке, то на какой прямой лежит эта точка?

+ на прямой, что проходит через центры окружностей

— на прямой, перпендикулярной радиусам окружностей

— на прямой, соединяющей центры вписанных в окружности треугольников

17. Как вычислить длину окружности через радиус?

18. Чему равно кратчайшее расстояние от центра окружности к касательной?

— квадратному корню из диаметра

— медиане вписанного треугольника

19. Секущая окружности – это:

— одна из сторон описанного треугольника

— прямая, параллельная диаметру окружности

— хорда, которая равна радиусу окружности

+ прямая, которая проходит через 2 точки окружности

тест-20. Если радиус окружности перпендикулярен к хорде, то он… Закончите утверждение:

— равен длине хорды

+ разделяет хорду пополам в точке их пересечения

— делит хорду в отношении 1:2

— делится пополам в точке пересечения с хордой

21. Что такое центральный угол окружности?

— угол, вершина которого лежит на окружности, а стороны угла пересекают окружность

— угол, равный 60 0

+ угол, вершиной которого является центр окружности

— угол, одна из сторон которого проходит через центр окружности

22. Если вписанный угол равен 90 0 , то он… Закончите утверждение:

+ опирается на диаметр

— имеет равные стороны

— имеет сторону, проходящую через центр окружности

— имеет сторону, равную радиусу

23. Как называется часть окружности, которая соединяет 2 точки на окружности?

24. Как измеряется вписанный угол?

— равен дуге, на которую он опирается

— равен центральному углу, опирающемуся на ту же дугу

+ равен половине дуги, на которую он опирается

25. Если вписанные углы опираются на одну дугу, то они… Закончите утверждение:

+ равны между собой

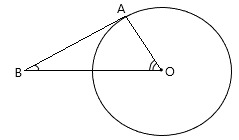
26. Дана окружность с центром O. AB – касательная к окружности. Угол ABO=33 0 , чему равен угол BOA?

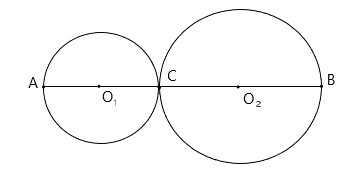
27. Даны две окружности с центрами O₂ и O₁, которые касаются в точке C. Радиус меньшей окружности равен 4 см, длина отрезка AB=20 см. Чему равен радиус большей окружности?

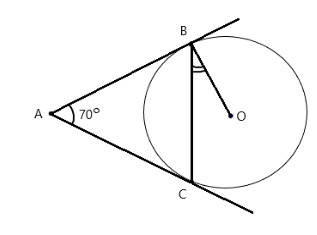
28. Лучи AB и AC касаются окружности с центром О в точках B и C. Угол BAC=70 0 . Найдите угол OBC.

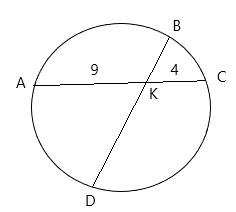
29. Найдите длину хорды BD, если AK=9 см, KC=4 см, BK:KD = 1:4.

тест_30. A – точка касания окружности с центром O и прямой AB. OA=9 см, AB=12 см. Найдите длину отрезка CB.

Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Вопросы и тест к зачету по теме «Окружность» в 8-9 классах

Видео:Геометрия. Окружность с нуля. Основы. Теоремы и задачи (примеры). 7 класс.Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Вопросы к зачету по теме «Окружность»

Взаимное расположение прямой и окружности (все случаи в зависимости от соотношения между радиусом окружности и расстоянием от центра окружности до прямой). Секущая.

Касательная к окружности, определение. Свойство касательной. Признак касательной.

Теорема об отрезках касательных, проведенных из одной точки к окружности.

Построение касательной к окружности, проведенной через данную точку (два случая: точка лежит на окружности и точка – вне окружности).

Определение центрального и вписанного углов.

Градусная мера дуги, обозначение, измерение.

Теорема о величине вписанного угла (рассмотреть 3 случая).

Свойство вписанных углов, опирающихся на одну и ту же дугу (хорду).

Теорема о свойстве отрезков двух пересекающихся хорд окружности.

Четыре замечательные точки треугольника.

Теорема о точке пересечения биссектрис треугольника. Теорема о вписанной в треугольник окружности.

Теорема о точке пересечения высот треугольника – ортоцентре.

Теорема о точке пересечения медиан треугольника – центре тяжести.

Серединный перпендикуляр к отрезку и его свойство. Теорема о точке пересечения серединных перпендикуляров к сторонам треугольника. Теорема об описанной около треугольника окружности.

Вписанные и описанные многоугольники ( определения).

Теорема об описанном около окружности четырехугольнике (прямая и обратная).

Теорема о вписанном в окружность четырехугольнике (прямая и обратная).

Построение среднего пропорционального двух отрезков.

Теорема об отрезках касательной и секущей, проведенных из одной точки к окружности.

Теорема об отрезках секущих, проведенных из одной точки к окружности.

Теорема об угле между касательной и секущей, проведенных через одну точку окружности.

Теоремы об измерении углов с вершиной вне и внутри окружности.

Тест к зачету по теме «окружность»

Прямая и окружность имеют две общие точки, если расстояние от _________________________ до______________ _________меньше ___________________________.

Могут ли две касательные к одной окружности быть параллельными?___________________

Если прямая АВ – касательная к окружности с центром О и В – точка касания, то прямая АВ и _____________ ОВ _______________________________________________

Верно ли, что градусная мера дуги окружности может быть больше 180 градусов?___________

Верно ли, что если сумма градусных мер двух дуг окружности равна 360 градусам, то эти дуги имеют общие концы?___________

Могут ли вписанные углы, опирающиеся на одну и ту же дугу, не быть равными?___________

Определите, является ли треугольник АВМ остроугольным, прямоугольным или тупоугольным, если точки А и В – концы диаметра окружности, а точка М лежит на окружности?__________________

Определите, является ли вписанный угол АВС острым, прямым или тупым, если точка Р лежит на дуге АВС и угол АРС – острый?____________________________

Может ли градусная мера центрального угла быть меньше градусной меры соответствующей ему дуги?_________________________

Если вписанный угол опирается на диаметр, то __________________________________

Если угол ABD – вписанный, а AOD – центральный, то ABD = —- AOD .

Если отрезки АВ и АТ отрезки касательных к окружности, то __________________________________

Если хорды AB и CD пересекаются в точке Е, то верно равенство:_____________

Если AB — касательная, AD – секущая и АМ — ее внешняя часть, то справедливо равенство:___________________________________________

Центром окружности, вписанной в треугольник, является точка___________________________________________________________________

Если точка равноудалена от сторон угла, то она лежит на _____________________________________

Если точка лежит на серединном перпендикуляре, проведенном к данному отрезку, то она_____________________________________________________________________

Около любого ___________________________можно описать окружность. Ее центром является точка пересечения_____________________________ , т.к. она равноудалена от __________________________

Точка пересечения ________________ треугольника делит их в отношении _________, считая от _________________

Если центром вписанной в треугольник окружности является точка пересечения медиан, то этот треугольник а) прямоугольный, б) равнобедренный, в) равносторонний

Определите вид треугольника, если центр описанной окружности лежит на одной из его сторон._____________________________

Определите вид треугольника, если точка пересечения его высот совпадает с вершиной треугольника __________________________

Определите, около какого параллелограмма ( не являющегося квадратом) всегда можно описать окружность_________________________

Определите, каким свойством должны обладать диагонали прямоугольника, чтобы в него можно было вписать окружность___________________________________________________________

Каким свойством должен обладать четырехугольник, чтобы около него можно было описать окружность?______________________________________________________________________

Если в четырехугольник ABCD вписана окружность, то_____________________________

Треугольник вписан в окружность. Определите его вид, если ни одна из его сторон не больше диаметра окружности____________________________________________

Даны две трапеции. Известно, что около первой нельзя описать окружность, а во вторую нельзя вписать окружность. Какая из этих трапеций может быть равнобедренной?__________________

Тест к зачету по теме «окружность»

Прямая и окружность имеют только одну общую точку, если расстояние от _________________________ до______________ _________равно ___________________________.

Могут ли две касательные к одной окружности быть перпендикулярными?___________________

Если прямая АВ проходит через конец радиуса ОК и АВ перпендикулярна ОК, то АВ является ______________________________ к данной окружности.

Верно ли, что градусная мера центрального угла может быть больше 180 градусов?___________

Верно ли, что если две различные дуги имеют общие концы, то сумма их градусных мер равна 360 градусам?___________

Могут ли два вписанных угла быть равными, если они опираются на разные дуги?__________________________________

Определите, является ли треугольник АВМ остроугольным, прямоугольным или тупоугольным, если АВ и АС – хорды окружности, а дуга АВС меньше полуокружности?__________________

Определите, является ли вписанный угол АВС острым, прямым или тупым, если точка Р лежит на дуге АВС и угол АРС –тупой?____________________________

Может ли градусная мера вписанного угла быть больше градусной меры соответствующей ему дуги?_________________________

Если вписанный угол опирается на диаметр, то __________________________________

Если угол AB С – вписанный, а AO С – центральный, то AB С= —- AO С.

Если хорды МР и ТК пересекаются в точке Е, то верно равенство:_____________

Если ВМ и ВТ – отрезки касательных к окружности, то________________________________________

Если ТН — касательная, ТМ– секущая и ТК — ее внешняя часть, то справедливо равенство:___________________________________________

Центром окружности, описанной около треугольника, является точка___________________________________________________________________

Если точка лежит на биссектрисе угла, то она_____________________________________

Если точка равноудалена от концов отрезка, то она лежит на __________________________________

В любой ___________________________можно вписать окружность. Ее центром является точка пересечения_____________________________ , т.к. она равноудалена от __________________________

Точка пересечения ________________ треугольника делит их в отношении _________, считая от _________________

Если центром вписанной в треугольник окружности является точка пересечения высот , то этот треугольник а) прямоугольный, б) равнобедренный, в) равносторонний

Определите вид треугольника, если центр описанной окружности лежит на одной из его сторон._____________________________

Определите вид треугольника, если точка пересечения его высот совпадает с вершиной треугольника __________________________

Определите, в какой параллелограмм ( не являющегося квадратом) всегда можно вписать окружность_________________________

Определите, каким свойством должны обладать диагонали ромба, чтобы около него можно было описать окружность___________________________________________________________

Каким свойством должен обладать четырехугольник, чтобы около него можно было описать окружность?______________________________________________________________________

Если в четырехугольник МРТК вписана окружность, то_____________________________

Треугольник вписан в окружность. Определите его вид, если диаметр окружности меньше любой из его сторон ____________________________________________

Даны две трапеции. Известно, что около первой можно описать окружность, а во вторую можно вписать окружность. Какая из этих трапеций может быть прямоугольной?__________________

Видео:Задача на окружности из ОГЭ-2023!! Разбор за 30 секСкачать

Дистанционные курсы для педагогов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 927 человек из 80 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 321 человек из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 700 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Зачеты — форма организации контроля и учета успеваемости учащихся, они решают задачи систематизации, углубления и закрепления знаний, умений и навыков по важнейшим разделам и темам программы, готовят учащихся к сдаче итогового экзамена. Цель учителя – добиться того, чтобы каждый учащийся овладел важнейшими умениями и навыками. Поэтому, если ученик не справился с зачетом, надо организовать доработку соответствующего материала, и его повторную проверку.

Данный зачет проводится в завершении темы «Окружность» письменно на уроке и подразумевает проверку знаний теории. Практическая часть зачета предусматривается на другом уроке. Проверяются как знания базового уровня так и повышенного . Это дает возможность учителю судить о готовности или неготовности каждого ученика к дальнейшему продвижению по курсу, скорректировать дальнейшую работу, выявив учащихся с затруднениями и пробелами, а также тех, кто усвоил материал на высоком уровне; определить эффективность организации, методов и средств обучения; выявить степень правильности, объем, глубину усвоенных знаний. Зачет развивает у учащихся умение анализировать, систематизировать информацию, воспитывает серьезное отношение к обучению и формирует умение оценивать свой уровень знаний и стремление повышать его. Круг вопросов, вынесенных на зачет, и дата зачета известны учащимся задолго до проведения зачета. В ходе подготовки к зачету обсуждаются и решаются задачи разного уровня: базового и повышенного, задаются и обсуждаются дифференцированные домашние контрольные работы разного уровня сложности.

Зачет оценивается отметками от 3 до 5 или «незачтено» по количеству набранных баллов за каждый из ответов.

💡 Видео

Окружность | Геометрия 7-9 класс #22 | ИнфоурокСкачать

Бестселлер Все правила по геометрии за 7 классСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

УРАВНЕНИЯ ОКРУЖНОСТИ И ПРЯМОЙ 9 класс геометрияСкачать

ОГЭ 2023 математика 16 задание окружность квадрат площадьСкачать

КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать