Частица движется по окружности с тангенциальным ускорением

4. Частица начинает двигаться по окружности с постоянным тангенциальным ускорением. Найти угол между скоростью и ускорением после первого оборота. Начальная скорость точки равна нулю.

Пусть радиус окружности R, тангенциальное ускорение a.

Тогда линейная скорость зависит от времени по закону v = at;

Пройденный путь: s = atІ/2.

После первого оборота s = 2рR ⇒ t =2
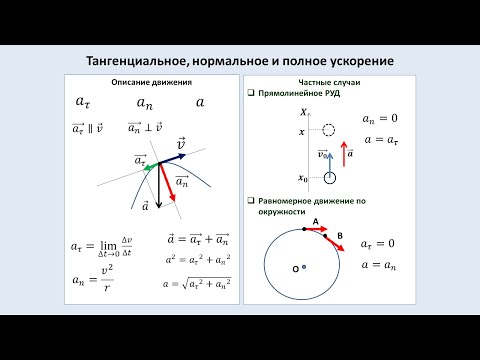
Полное ускорение равно сумме нормального (центростремительного) и тангенциального ускорений (направленных перпендикулярно друг другу):
aΣ = aц + aт
Вектор скорости v направлен по касательной, то есть параллельно тангенциальному ускорению и перпендикулярно центростремительному.

Поскольку векторы скорости и тангенциального ускорения сонаправленны, то угол б между векторами скорости и полного ускорения равен углу между векторами тангенциального и полного ускорений; если сделать рисунок, видно, что тангенс этого угла равен отношению модуля центростремительного ускорения к модулю тангенциального ускорения.

Центростремительное ускорение после первого оборота равно
aц = vІ/R = (at)І/R = aІ•(4πR/a)/R = 4πa,
тогда б = arctg(aц/a) = arctg(4р) = arctg(4⋅3,14) ≈ 85,5°

8. Тело движется по горизонтальной плоскости под действием силы F, направленной под углом б к горизонту (рис). Найти ускорение тела, если его масса m, а коэффициент трения между телом и плоскостью μ. При каком значении силы F движение будет равномерным?

Согласно второму закону Ньютона :

где равнодействующая сила

Проекции на оси:

Х:

У:

Движение будет равномерным при а = 0.

10. Через неподвижный блок перекинута нить, к которой подвешены три одинаковых груза массой m=5кг каждый (рис). Найти ускорение системы и силу натяжения нити между грузами 1 и 2. Какой путь пройдет груз за первые t=4 с движения? Трением пренебречь.

Так как масса m2 второго тела больше массы m1первого, то второе тело будет опускаться, а первое — подниматься.

Складывая уравнения системы, приходим к равенству:

Видео:Центростремительное ускорение. 9 класс.Скачать

Частица движется по окружности, при этом ее скорость изменяется по закону w(омега) = 2r ^ 2?

Физика | 10 — 11 классы

Частица движется по окружности, при этом ее скорость изменяется по закону w(омега) = 2r ^ 2.

Найдите отношение нормального ускорения точки к её тангенциальному ускорению спустя 2 сек после начала движения.

a₁ — нормальное ускорение

а₂ — тангенциальное ускорение

Формула нормального ускорения :

Формула линейной скорости :

Формула тангенциального ускорения

a₂ = dv / dt = r dw / dt

a₂ = r (2r²)’ = r 2r²t = 2r³t

Находим искомое соотношение

a₁ / a₂ = 4r⁵ : 2r³t = 2r³t

a₁ / a₂ = 2r³ * 2 = 4r³

Видео:Физика - движение по окружностиСкачать

Точка движется по окружности R = 20 см с постоянным тангенциальным ускорением a = 5 * 10 ^ — 2 м / с?

Точка движется по окружности R = 20 см с постоянным тангенциальным ускорением a = 5 * 10 ^ — 2 м / с.

Через какое время после начала движения нормальная составляющая проекция полного ускорения будет равна тангенциальной составляющей?

Видео:Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

Помогите пожалуйста?

) материальная точка движется по окружности радиусом R = 1 м так, что величина ее скорости изменяется по закону v = 4 + 2t.

Определить нормальное, тангенциальное и полное ускорения в момент времени t = 2c.

Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Точка движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением a найти тангенциальное ускорение a точки, если известно, что к концу пятого оборота после начала движения линейна?

Точка движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением a найти тангенциальное ускорение a точки, если известно, что к концу пятого оборота после начала движения линейная скорость точки достигла значения V = 79, 2 см / с.

Видео:Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

Помогите пожалуйста?

Материальная точка движется по окружности радиусом R с постоянным тангенциальным ускорением ат.

Через какое время t после начала движения центростремительное ускорение аn будет больше ат в n раз?

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Материальная точка движется по окружности, диаметр которой равен 40м?

Материальная точка движется по окружности, диаметр которой равен 40м.

Зависимость пути от времени ее движения определяется уравением s = t ^ 3 + 4t ^ 2 — t + 8.

Определить пройденный путь, скорость, нормальное, тангенциальное и полное ускорения через 39с от начала движения точки по окружности.

Построить векторную диаграмму скорости и ускорения.

Видео:Рассмотрение темы: "Тангенциальное, нормальное и полное ускорение"Скачать

Точка движется по окружности с постоянной скоростью 0, 5м / с?

Точка движется по окружности с постоянной скоростью 0, 5м / с.

Вектор скорости изменяет направление на Δφ = 30° за 2с.

Каково Нормальное ускорение точки?

Видео:Лекция 6.5 | Нормальное и тангенциальное ускорение | Александр Чирцов | ЛекториумСкачать

Физика Модератор IUV Помогите Точка начинает двигаться равноускорено по окружности?

Физика Модератор IUV Помогите Точка начинает двигаться равноускорено по окружности.

5c после начала движения нормальное и тангенциальное ускорение сравнялись.

Определить угловую скорость для этого момента времени.

Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

По дуге окружности радиуса 10 м движется точка?

По дуге окружности радиуса 10 м движется точка.

В некоторый момент времени нормальное ускорение точки равен 4, 9 м / с2 ; вектор полного ускорения образует в этот момент с вектором нормального ускорения угол 60 .

Найти скорость и тангенциальное ускорение точки.

Видео:Формулы механики 2, движение по окружности, центростремительное ускорениеСкачать

Материальная точка двигается по спирали, как показано на рис?

Материальная точка двигается по спирали, как показано на рис.

Если точка двигается с постоянной скоростью, то .

Тангенциальное ускорение нормальное ускорение полное ускорение?

Видео:КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

1. Материальная точка движется по окружности радиуса 0, 2м без начальной скорости с постоянным тангенциальным ускорением 5см / с2?

1. Материальная точка движется по окружности радиуса 0, 2м без начальной скорости с постоянным тангенциальным ускорением 5см / с2.

Через какое время после начала движения нормальная составляющая ускорение будет равна 10см / с2?

Чему равен угол между векторами скорости и ускорения в этот момент?

Вы открыли страницу вопроса Частица движется по окружности, при этом ее скорость изменяется по закону w(омега) = 2r ^ 2?. Он относится к категории Физика. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Физика, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Виды движения по окружности

Угловое движение можно условно разделить на два вида:

1. Когда изменяется только направление вектора линейной скорости, а его длина не изменяется.
2. Или, когда изменяются обе характеристики вектора линейной скорости.

Во втором случае, для описания движения будем применять более сложные формулы кинематики. Так как появится еще один вид ускорения.

Центростремительное (нормальное) ускорение есть всегда, когда есть движение по окружности, при этом не важно, меняется ли скорость тела по модулю, или не меняется.

Видео:Урок 89. Движение по окружности (ч.1)Скачать

Движение по окружности с постоянной по модулю скоростью

Пусть тело движется по окружности, но при этом длина вектора линейной скорости не меняется (рис. 1).

[left|vec right| = const]

На рисунке 1 указаны: а) – вид сбоку, б) вид сверху, вектор угловой скорости направлен к нам перпендикулярно рисунку.

Скорость будет меняться только по направлению от точки к точке, потому, что на тело действует центростремительная сила (displaystyle vec<F_<text>>) , тело обладает центростремительным (displaystyle vec<a_<text>>) (нормальным) ускорением.

Кроме линейной, тело обладает угловой скоростью. Если линейная скорость не изменяется по модулю, то длина вектора угловой скорости не меняется.

На рисунке 1а изображен вектор угловой скорости (displaystyle vec), на рисунке 1б вектор угловой скорости направлен к нам перпендикулярно плоскости рисунка. Направление, в котором тело движется по окружности, указано синей стрелкой.

Видео:Физика 9 класс (Урок№4 - Движение тела по окружности. Период и частота)Скачать

Тангенциальное ускорение – когда модуль скорости меняется

Тело может увеличивать или уменьшать свою скорость, когда движется по окружности.

В таком случае, дополнительно к нормальному ускорению возникает тангенциальное (displaystyle vec<a_>) ускорение.

Тангенциальное ускорение играет роль линейного ускорения при прямолинейном движении тела. Вектор (displaystyle vec<a_>) направлен параллельно вектору (displaystyle vec) скорости.

Подобно движению по прямой, вектор ускорения – это первая производная скорости по времени, или вторая производная перемещения по времени.

Когда векторы скорости (vec) и ускорения (vec<a_>) сонаправлены (рис. 2), линейная и угловая скорости возрастают.

А когда ускорение (vec<a_>) направлено противоположно (рис. 3) вектору скорости (vec), угловая и линейная скорости уменьшаются.

С линейной скоростью (vec) связана угловая (vec) скорость.

Из рисунков 2, 3 следует: когда появляется тангенциальное ускорение, меняется и угловая скорость. Значит, тангенциальное ускорение (vec<a_>) появляется совместно с угловым (vec) ускорением и между ними есть связь.

Связь между тангенциальным и угловым ускорением выглядит аналогично связи между линейной и угловой скоростью.

В векторном виде

В скалярном виде

[ large boxed < a_= beta cdot R >]

(displaystyle vec left( frac<text><c^>right)) – угловое ускорение;

(displaystyle vec< a_> left( frac<text><c^>right)) – тангенциальное ускорение;

(R left( textright)) – радиус окружности.

Видео:Движение тел по окружностиСкачать

Равноускоренное движение по окружности

Угловая скорость увеличивается (рис. 2), когда угловое ускорение сонаправлено с вектором угловой скорости. Когда движение происходит с постоянным ускорением, его называют равноускоренным.

Для решения задач на равноускоренное движение по окружности, поступаем аналогично равноускоренному движению по прямой. Применяем систему из двух уравнений:

[ large boxed < beginomega = omega _ + beta cdot t \ displaystyle varphi = omega_ cdot t + beta cdot frac end > ]

Первое уравнение системы – это связь между начальной (omega_ ) и конечной (omega ) скоростью. Второе уравнение – это уравнение движения.

Видео:Физика | Равномерное движение по окружностиСкачать

Равнозамедленное движение по окружности

Когда векторы (vec) и (vec) направлены в противоположные стороны, угловая скорость (vec) уменьшается (рис. 3).

Для решения задач кинематики, в которых угловая скорость уменьшается и, движение равнозамедленное, используем систему, состоящую из таких уравнений:

[ large boxed < beginomega = omega _ — beta cdot t \ displaystyle varphi = omega_ cdot t — beta cdot frac end > ]

Видео:Физика 9 класс. Движение по окружностиСкачать

Общее ускорение при движении по окружности

Пусть точка движется по окружности и линейная (vec) скорость ее изменяется по модулю. При этом, точка обладает двумя видами ускорения — нормальным и тангенциальным. Эти виды ускорения обозначают символом (vec).

Примечание: Любое ускорение, обозначаемое символом «a», измеряется в метрах, деленных на секунду в квадрате.

Направление вектора общего ускорения указано на рисунке 4а, а для равнозамедленного – на рисунке 4б.

Так как векторы (vec<a_>) и (vec<a_>) всегда перпендикулярны, длину вектора общего ускорения (vec) можно найти из теоремы Пифагора:

🎦 Видео

Движение по окружности | Физика в анимациях | s01e07Скачать

Олимпиадная физика, кинематика: решение задачи на движение по окружности с ускорением | 9–11 классСкачать

Нормальное и тангенциальное ускорениеСкачать