Вневписанная в треугольник abc окружность касается

Условие

Вневписанная в треугольник АВС окружность касается его боковой стороны и продолжения основания АС.

а) Докажите, что радиус этой окружности равен высоте ВН треугольника АВС.

б) Найдите площадь треугольника АВС, если радиус окружности равен 4, а АС*АВ = 30.

Решение

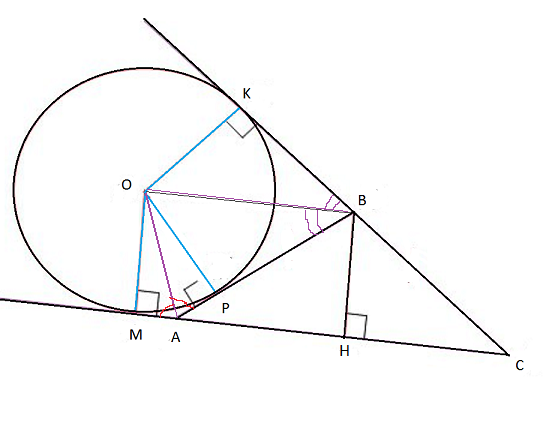
Вневписанная окружность — окружность, которая касается одной стороны треугольника и продолжений двух других сторон.
Центр этой окружности — точка пересечения биссектрис внешних углов.
При этом треугольник — произвольный.
В условии задачи речь идет об основании и боковой стороне. Значит, треугольник АВС — равнобедренный.
АВ=ВС.
Тогда высота ВН- равнобедренного треугольника АВС является и биссектрисой угла В, поэтому биссектрисы смежных углов ОВ и ВН — взаимно перпендикулярны.
Четырехугольник ОМВН — прямоугольник.
ВН=ОМ

б) Радиус окружности равен 4, значит по доказанному в а) ВН=4
и по условию АС·АВ = 30.
Так как треугольник АВС — равнобедренный,
АС=2АН.
Тогда условие принимает вид:
АС·АВ=АB·2АН;
АB·2АН=30;
АB·АН=15 ⇒ АB=15/AH.

По теореме Пифагора из прямоугольного треугольника АВН:
АВ^2=АН^2+ВН^2
(15/AH)^2=AH^2+4^2
Биквадратное уравнение
АН^4+16AH^2-225=0
D=16^2+4·225=256+900=1156=34^2
AH^2=(-16+34)/2=9
AH=3
S(Δ АВС)=АС·ВН/2=(AC/2)·ВН=AH·ВН=3·4=12
О т в е т. 12

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вневписанная в треугольник abc окружность касается

Видео:Вневписанная окружностьСкачать

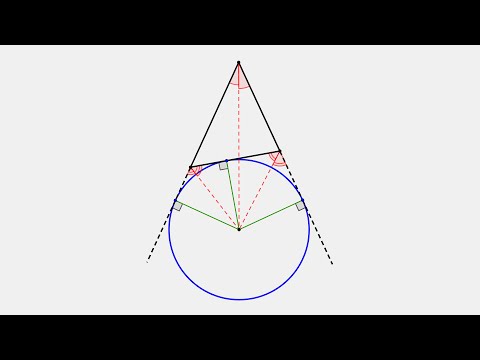
Источник задания: Решение 4951. ЕГЭ 2016 Математика, И.В. Ященко. 36 вариантов. Ответ.

Задание 16. Вневписанная окружность равнобедренного треугольника касается его боковой стороны.

а) Докажите, что радиус этой окружности равен высоте треугольника, опущенной на основание.

б) Известно, что радиус этой окружности в 6 раз больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной окружности с боковой стороной треугольника делит эту сторону?

а) Пусть вписанная окружность с центром О касается боковой стороны АВ и основания ВС равнобедренного треугольника ABC в точках М и H, а окружность с центром О1 касается боковой стороны АВ, продолжения основания ВС в точке D и продолжения боковой стороны АС в точке Е. Тогда АН — высота треугольника ABC.

Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому АO1 — биссектриса угла ВАЕ. В четырёхугольнике AHDO1 угол НАО1 — прямой как угол между биссектрисами смежных углов ВАС и ВАЕ, а так как , то АНDO1 — прямоугольник, поэтому O1D = АН.

б) Пусть радиус окружности с центром О равен r. Тогда радиус окружности с центром O1 равен 6r.

Из прямоугольного треугольника АОМ находим, что

Прямоугольные треугольники АОМ и АВН подобны по двум углам, поэтому

,

.

По теореме об отрезках касательных, проведённых к окружности из одной точки, . Следовательно,

Видео:Вневписанная окружностьСкачать

Вневписанная окружность треугольника АВС касается стороны ВС в точке М, продолжений сторон АВ и АС — в точках N и P соответственно.

Видео:№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

Ваш ответ

Видео:Вневписанная окружность треугольникаСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,909
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

🔥 Видео

Егэ c4. Вневписанная окружностьСкачать

✓ Как вневписанная окружность Герону помогла | Ботай со мной #083 | Борис ТрушинСкачать

Вневписанная окружность | Теоремы об окружностях - 3Скачать

#221. ЛЮТАЯ ДИЧЬ с IMO (математика)Скачать

Вневписанная окружность. Теория | Профильная математика в онлайн - школе СОТКАСкачать

Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

Задача про две вневписанные окружности | ЕГЭ. Задание 16. Математика | Борис Трушин |Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Задание 26 Вневписанная окружностьСкачать

Вписанные, описанные, вневписанные окружностиСкачать

ВТОРОЙ ЧЕРНЫЙ КОФЕ и вневписанная окружность!Скачать

Разбор Задачи №16 из Варианта Ларина №282Скачать

[11] Окружности с нуля для ЕГЭ по математике. Вневписанная окружность Теория и практика 13 задач.Скачать

Найти периметр треугольника. Вневписанная окружностьСкачать