Внешние углы треугольника 7 класс

Средняя оценка: 4.6

Всего получено оценок: 169.

Средняя оценка: 4.6

Всего получено оценок: 169.

Внешний угол треугольника редко используется при решении геометрических задач. Однако при этом свойства внешнего угла лучше знать, потому как задача на применение этих свойств рано или поздно попадется каждому ученику.

Видео:Внешний угол треугольникаСкачать

Внешний угол

Внешний угол треугольника это угол, смежный с внутренним. Внутренних углов в треугольнике три, и их сумма равна 180 градусам. Смежными углами зовутся углы, одна из сторон каждого лежит на одной прямой, а вторая является общей.

Что нужно сделать, чтобы увидеть внешний угол треугольника? Для этого придется выполнить некоторые дополнительные построения. Чтобы увидеть внешний угол треугольника необходимо продолжить его сторону. При каждой вершине две стороны, соответственно продолжить можно две прямых, и смежных углов будет два.

Итого в треугольнике получается 6 внешних углов.

Нежелательно на рисунке строить два внешних угла при одной вершине одновременно. Это усложнит построение и, чаще всего, не принесет никакого положительного результата.

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Свойства внешних углов

Свойств у внешних углов треугольника не так много и все они связаны с определением внешнего угла.

Основное свойство гласит, что внешний угол треугольника равен сумме двух внутренних углов не смежных с ним. Свойство доказывается достаточно просто. Сумма смежных углов равна 180. Сумма углов в треугольнике все те же 180. Тогда, если обозначить внутренние углы а,в,с, внешний угол d, то:

Вычтем из первого выражения второе и получим:

d=в+с – вот и все доказательство.

Рис. 2. Рисунок к доказательству.

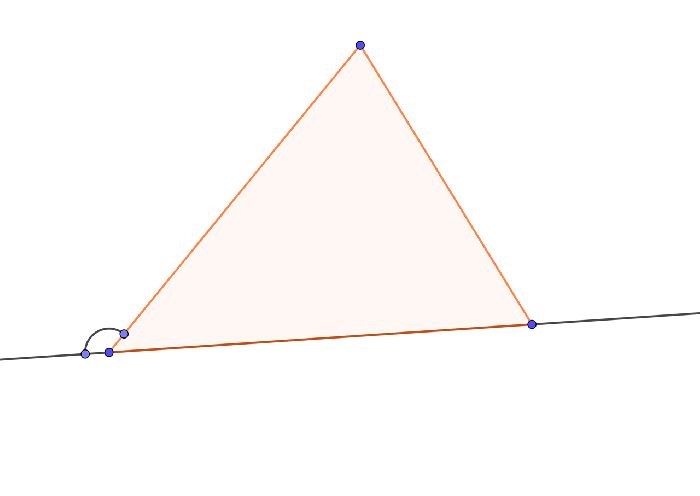
Есть еще несколько дополнительных свойств внешних углов:

• Если решение задачи требует одновременного существования двух внешних углов при одной вершине на чертеже, то можно заметить, что эти внешние углы будут равны, как вертикальные.
• Сумма трех внешних углов, по одному при каждой из вершин, равна 360 градусам.
• Так как внешний и внутренний углы треугольника смежные, то их сумма равна 180 градусам.

Особенное значение имеют внешние углы при решении тупоугольных треугольников. Дело в том, что в тупоугольном треугольнике одна из высот всегда внешняя. Найти эту высоту можно через тригонометрические функции. Для этого и нужно знать угол, который для тупоугольного треугольника будет внешним, а для достроенного прямоугольного треугольника – внутренним.

Видео:7 класс. Внешний угол треугольника.Скачать

Что мы узнали?

Мы привели определение внешнего угла треугольника. Посчитали количество внешних углов треугольника, определили особенности построения внешних углов при решении задачи. Рассказали, где чаще всего применяются свойства внешних углов треугольника.

Видео:Внешний угол треугольникаСкачать

Презентация по геометрии на тему: «Внешний угол треугольника» (7 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

«Внешний угол треугольника»

Ворожейкина Татьяна Евтифьевна
учитель математики
МОУ-СОШ с.Журавлевка

Найти неизвестные углы в ΔАВС

Определение. Внешним углом треугольника называют угол, смежный с углом треугольника

Внешний угол треугольника
Теорема. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

Упражнение 1
В треугольнике ABC угол A равен 40o, внешний угол при вершине B равен 100o. Найдите угол C.
Ответ: 60о.

Упражнение 2
В треугольнике ABC угол A равен 40o. Внешний угол при вершине B равен 70o. Найдите угол C.
Ответ: 30о.

Упражнение 3
В треугольнике ABC AC = BC, угол C равен 50o. Найдите внешний угол CBD.
Ответ: 115о.

Упражнение 4
В треугольнике ABC AC = BC. Внешний угол при вершине B равен 120o. Найдите угол C.
Ответ: 60о.

Упражнение 5
В треугольнике ABC AB = BC. Внешний угол при вершине B равен 140o. Найдите угол C.
Ответ: 70о.

Упражнение 6
Один из внешних углов треугольника равен 80о. Углы, не смежные с данным внешним углом, относятся как 2:3. Найдите наибольший из них.
Ответ: 48о.

Упражнение 7
Сумма двух углов треугольника и внешнего угла к третьему равна 30o. Найдите этот третий угол.
Ответ: 165o.

Внешний угол треугольника равен сумме
двух углов треугольника, не смежных с ним.
А
В
С
К
1
2
СВК
2
1
=
+
Повторение

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 991 человек из 78 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 672 человека из 74 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 307 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Видео:7 класс. Сумма углов треугольника. Внешние углы треугольника. Контрольная работа А1-А2. Ершова А.П.Скачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 543 423 материала в базе

Материал подходит для УМК

«Геометрия», Мерзляк А.Г., Полонский В.Б., Якир М.С./ Под ред. Подольского В.Е.

§ 16. Сумма углов треугольника

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 05.02.2022
• 72
• 6

• 05.02.2022
• 144
• 5

• 05.02.2022
• 37
• 0

• 05.02.2022
• 42
• 0

• 05.02.2022
• 56
• 0

• 05.02.2022
• 53
• 0

• 05.02.2022
• 29
• 0

• 05.02.2022
• 201
• 3

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 05.02.2022 69
• PPTX 1.4 мбайт
• 6 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Ворожейкина Татьяна Евтифьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет
• Подписчики: 0
• Всего просмотров: 24676
• Всего материалов: 41

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:теорема о внешнем угле треугольника. Доказательство.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Томске студентов вузов перевели на дистанционное обучение до конца февраля

Время чтения: 1 минута

Петербургских школьников с 7 по 11 классы перевели на дистанционное обучение

Время чтения: 1 минута

В Госдуме предложили ввести пост уполномоченного по правам учителей

Время чтения: 2 минуты

Пермский Роспотребнадзор предписал перевести обучение в школах и ссузах на дистант

Время чтения: 2 минуты

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Петербургская учительница уволилась после чтения на уроке Введенского и Хармса

Время чтения: 3 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Медианы, биссектрисы и высоты треугольника | Геометрия 7-9 класс #18 | ИнфоурокСкачать

Внешний угол треугольника

Внешний угол треугольника — это угол, смежный с любым из внутренних углов треугольника.

При каждой вершине треугольника может быть построено по два равных внешних угла. Например, если продолжить все стороны треугольника ABC, то при каждой его вершине получится по два внешних угла, которые равны между собой, как вертикальные углы:

Из данного примера можно сделать вывод, что внешние углы, построенные при одной вершине, будут равны.

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Так как внешний угол (∠1) дополняет внутренний угол (∠4) до развёрнутого угла, то их сумма равна 180°:

Сумма внутренних углов углов любого треугольника тоже равна 180°, значит:

Из этого следует, что

Сократив обе части полученного равенства на одно и тоже число (∠4), получим:

Из этого можно сделать вывод, что внешний угол треугольника всегда больше любого внутреннего угла, не смежного с ним.

Видео:Геометрия за 6 минут — Сумма углов треугольника и Внешний УголСкачать

Сумма внешних углов

Сумма трёх внешних углов треугольника, построенных при разных вершинах, равна 360°

Рассмотрим треугольник ABC:

Каждая пара углов (внутренний и смежный с ним внешний) в сумме равны 180°. Все шесть углов (3 внутренних и 3 внешних) вместе равны 540°:

(∠1 + ∠4) + (∠2 + ∠5) + (∠3 + ∠6) = 180° + 180° + 180° = 540°.

Значит чтобы найти сумму внешних углов, надо из общей суммы вычесть сумму внутренних углов:

∠1 + ∠2 + ∠3 = 540° — (∠4 + ∠5 + ∠6) = 540° — 180° = 360°.

📹 Видео

Высота, биссектриса, медиана. 7 класс.Скачать

РЕШЕНИЕ ЗАДАЧИ ПО ТЕМЕ «ВНЕШНИЙ УГОЛ ТРЕУГОЛЬНИКА». Задачи | ГЕОМЕТРИЯ 7 классСкачать

Соотношения между сторонами и углами треугольника. 7 класс.Скачать

7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Американская задача для семиклассников, которая поставила в тупик родителейСкачать

7 класс. Внешний угол треугольникаСкачать

Внешний угол треугольникаСкачать

Внешний угол треугольника. Теорема о внешнем угле треугольника. Примеры задач. Геометрия 7 класс.Скачать

Сумма углов треугольника (доказательство). Внешний угол треугольника - 7 класс геометрияСкачать

Геометрия 7 класс (Урок№23 - Сумма углов треугольника.)Скачать

Урок 17. Внешний угол треугольника 7 классСкачать

№234. Один из внешних углов равнобедренного треугольника равен 115°. Найдите углы треугольника.Скачать