Вне прямоугольного треугольника на сторонах (8 видео)

Вне прямоугольного треугольника на сторонах

На сторонах AC, AB и BC прямоугольного треугольника ABC с прямым углом C вне треугольника ABC построены равнобедренные прямоугольные треугольники AKC, ALB и BMC с прямыми углами K, L и M соответственно.

а) Докажите, что LC — высота треугольника KLM.

б) Найдите площадь треугольника KLM, если LC = 6.

значит, четырёхугольник LACB вписанный. Хорды AL и LB описанной около четырёхугольника LACB окружности равны. Значит, равны между собой стягиваемые этими хордами дуги, а также опирающиеся на эти дуги вписанные углы ACL и LCB. Тогда углы ACL и LBC равны 45°.

По условию углы KCA и MCB равны 45°. Следовательно,

а значит, LC — высота треугольника KLM.

б) Для удобства обозначим отрезки буквами: BC — a, AC — b, AB — c и CL — d. Пусть P — точка пересечения CL и AB. Тогда по доказанному в пункте а) отрезок CP — биссектриса треугольника ABC. По свойству биссектрисы AP : PB = AC : CB = b : a, AP + PB = AB = c. Отсюда

Поскольку углы ACL и LBC равны 45°, получаем, что треугольники ACL и PAL подобны по двум углам, тогда

Площадь треугольника KLM равна половине произведения его высоты LC, обозначенной буквой d, на сторону, являющуюся основанием треугольника и равную

Следовательно, искомая площадь равна

Содержание

Деление пифагоровых штанов
Задача
Подсказка 1
Подсказка 2
Решение
Послесловие
Задача 45625 Вне прямоугольного треугольника АВС на.
Условие
Решение
💡 Видео

Видео:№1125. На сторонах прямоугольного треугольника как на диаметрах построены три полукруга.Скачать

Деление пифагоровых штанов

Видео:На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC Точка M — сереСкачать

Задача

На сторонах прямоугольного треугольника вне его построены три квадрата. Эту известную с давних времен картинку иногда называют «пифагоровы штаны». Постройте (циркулем и линейкой) еще один квадрат так, чтобы он делил площадь каждого из квадратов пифагоровых штанов пополам.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Подсказка 1

Пример подходящего расположения квадрата показан на рис. 1.

Видео:Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Подсказка 2

Прямая, проходящая через центр квадрата, делит его пополам.

Видео:ЕГЭ задание 16 Пять треугольниковСкачать

Решение

Если данный прямоугольный треугольник равнобедренный, то задача решается совсем просто. Поэтому будем считать, что его катеты разные.

Как часто делают при решении задач на построение, начнем с анализа: изучим ситуацию, в которой требуемый квадрат уже построен. Итак, пусть дан прямоугольный треугольник ABC с катетами BC = a и AC = b (без ограничения общности считаем, что a > b) и гипотенузой AB = c, на сторонах которого построены квадраты. Пусть О₁ и О₂ — центры квадратов, построенных на катетах (рис. 2). Расположим искомый квадрат KFMN так, чтобы его стороны KN и KF проходили через точки О₁ и О₂ параллельно катетам a и b, соответственно. Тогда вершина M этого квадрата лежит на биссектрисе угла FKN. Остается определить положение точки M на этой биссектрисе, учитывая, что площадь пятиугольника ABEMP должна быть равна половине площади квадрата со стороной c (то есть (a 2 + b 2 )/2). Пусть P и E — точки пересечения отрезков MF и MN с соответствующими сторонами этого квадрата.

Опустим перпендикуляры: MH на AB, PL и ET на MH. Тогда (angle EMT=angle MPL=angle ABC = beta).

Введем прямоугольную систему координат xAy. Пусть точка M имеет координаты (x, y), тогда выполнены равенства AH = PL = x, MH = y. В треугольнике PML имеем (ML=xmathrm,beta=xb/a), (AP=HL=y-xb/a). Так как (TE=BH=c-x), то в треугольнике EMT имеем: (MT=(c-x)mathrm,beta=(c-x)frac ab), тогда (BE=HT=y-(c-x)frac ab).

Площадь пятиугольника ABEMP — это сумма площадей трапеций APMH и BEMH. Значит, его площадь (которая должна быть равна (frac2)) равна сумме (frac12(AP+MH)cdot AH+frac12(BE+MH)cdot BH). После подстановок получаем важное уравнение:

Пусть Q — середина гипотенузы AB. Так как расстояние от точки Q до каждой из прямых KN и KF равно ((a+b)/2), то Q — точка пересечения KM и AB. Следовательно, отрезок KQ параллелен биссектрисе угла C треугольника ABC, то есть составляет угол (45^circ+beta) с положительным направлением оси x. Тогда ее угловой коэффициент равен (mathrm,(45^circ+beta)=frac<mathrm,45^circ+mathrm,beta><1-mathrm,45^circmathrm,beta >=frac.)

Учитывая, что точка Q имеет координаты (c/2, 0), получим уравнение этой прямой:

Решая систему, составленную из этого уравнения прямой и важного уравнения, находим, что точка M имеет следующие координаты:

Видео:№440* На двух сторонах треугольника вне его построены квадраты. Докажите, что отрезок, соединяющий Скачать

Послесловие

Построенный квадрат не единственный. На самом деле таких квадратов бесконечно много. Покажем это.

Очевидно, что можно построить бесконечно много прямых углов, стороны которых проходят через центры квадратов, построенных на катетах: их вершины лежат на окружности с диаметром О₁О₂. При этом вершины должны находиться на той дуге, которая лежит снаружи от обоих квадратов, построенных на катетах (и «между» ними). Рассмотрим один из таких углов (на рис. 3 этот угол нарисован красным). Построим квадрат, две стороны которого лежат на сторонах этого угла. Ясно, что тогда одна из вершин этого квадрата лежит на биссектрисе угла. Слева на рис. 3 показан самый маленький такой квадрат. Видно, что его стороны делят пополам площадь квадратов, построенных на катетах, а одна из его вершин лежит на стороне меньшего квадрата. При этом стороны красного квадрата отсекают у квадрата, построенного на гипотенузе, пятиугольник площадью чуть больше четверти его площади.

Если теперь «раздувать» красный квадрат, увеличивая его сторону, то площадь высекаемого пятиугольника будет непрерывно увеличиваться до площади, близкой к трем четвертям площади квадрата, построенного на гипотенузе. При этом одна из вершин делящего квадрата совпадет с точкой пересечения биссектрисы со стороной квадрата, построенного на гипотенузе (правое изображение на рис. 3). Таким образом, учитывая непрерывность функции площади, согласно теореме Больцано-Коши можно утверждать, что существует длина стороны делящего квадрата, при которой площадь пятиугольника будет равна половине площади квадрата, построенного на гипотенузе.

Благодаря этому можно привести более простое построение для треугольников, у которых длины катетов мало отличаются друг от друга.

Рассмотрим это построение, ограничившись анализом. Квадрат, построенный на гипотенузе, разобьем на 16 равных квадратов (рис. 4). Из узла M под углом 45° проведем перпендикулярные друг другу лучи MF и MN. Через центры О₁ и О₂ квадратов, построенных на катетах, проведем прямые FK и NK, параллельные лучам MN и MF, соответственно. Получим квадрат MNKF, делящий пополам площадь каждого из трех квадратов «пифагоровых штанов». Убедитесь в этом самостоятельно.

Эта задача предлагалась на XIII Творческом конкурсе учителей математики России. Участники конкурса выяснили, что такое построение возможно не для всех прямоугольных треугольников, а только для тех, у которых (mathrm,angle A), то есть отношение большего катета к меньшему, не превосходит числа t₀ = 1,8393. являющегося иррациональным корнем уравнения (t^2-t^2-t-1=0). Вершина K делящего квадрата попадает на границу квадрата, построенного на большем катете, если (mathrm,angle A=t_0). Если же (mathrm,angle A>t_0), то вершина K делящего квадрата попадает внутрь квадрата, построенного на большем катете, и тогда площадь этого квадрата не делится пополам.

В заключение добавлю, что задача родилась как некоторый аналог любопытного факта при чтении книги «Математический калейдоскоп» польского математика Г. Штейнгауза. В ней он утверждает, что на плоскости существует окружность, которая делит пополам площади трех областей произвольной формы и приводит на географической карте пример такой окружности, которая делит на равновеликие части три фигуры, являющиеся контурами Австрии, Польши и Румынии. Вспомнив про три квадрата «пифагоровых штанов» и заменив окружность четвертым квадратом, я сформулировал предложенную задачу.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

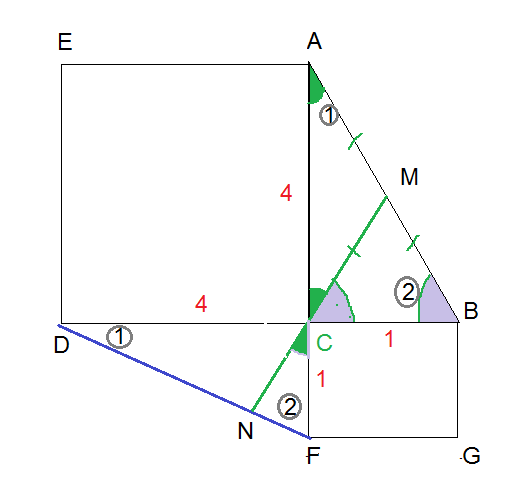
Задача 45625 Вне прямоугольного треугольника АВС на.

Условие

Вне прямоугольного треугольника АВС на его катетах АС и ВС построены квадраты ACDE и BCFG. Продолжение медианы СМ треугольника АВС пересекает прямую DF в точке N.

а) Докажите, что CN является высотой треугольника CDF.

б) Найдите отрезок CN, если AC = 1, BC = 4. [16п6]

Решение

В Δ АВС: АС- катет и ВС — катет ⇒ ∠ С=90 ° или ∠АСB=90 °

ACDE- квадрат ⇒ ∠ ACD=90 ° и АС=DC
BCFG- квадрат ⇒ ∠ BCF=90 ° и BС=CF

Прямоугольные треугольники СDF и ABC равны по двум катетам.
АС=DC =4
BС=CF=1

Значит и соответствующие углы в этих треугольниках равны
∠ BAC= ∠ CDF= ∠ 1 ( расположены против сторон ВС и СF)
∠ ABC= ∠ DFC= ∠ 2 ( расположены против сторон AD и DC)

∠ВАС= ∠ MСA= ∠ 1, так как медиана СМ прямоугольного треугольника равна половине гипотенузы и Δ АМС — равнобедренный
Аналогично
∠МВС= ∠ МСВ= ∠ 2.

∠ FCN=∠ МCA= ∠ 1 как вертикальные

Значит ∠ FCN+ ∠ CFN= ∠ 1+ ∠ 2 = 90 ° ⇒ ∠ СNF=90 °

По теореме Пифагора:
DF^2=DС^2+СF^2=1^2+4^2=17

S_( ΔDFC)=(1/2)DF*CN и S (ΔDFC)=(1/2)DC*CF, то

О т в е т. [b]4sqrt(17)/17[/b]