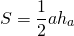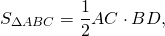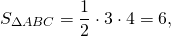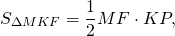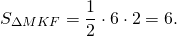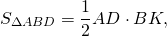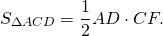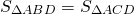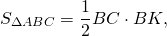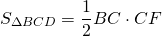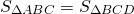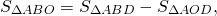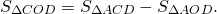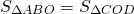Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать
Равновеликие треугольники
Равновеликие треугольники — это треугольники, которые имеют одинаковую площадь.
Равновеликие треугольники могут быть равными (так как равные треугольники имеют равные площади), но также могут иметь разные стороны и разные углы.
Например, треугольники ABC и MKF — равновеликие, так как их площади равны.
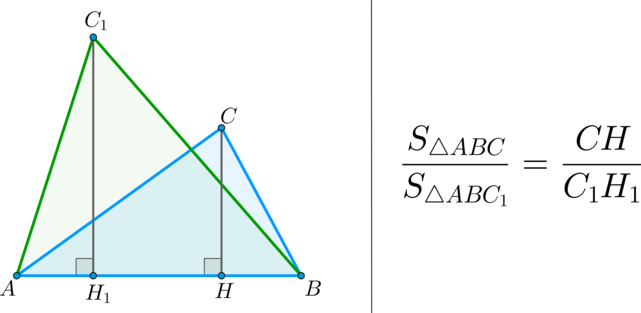
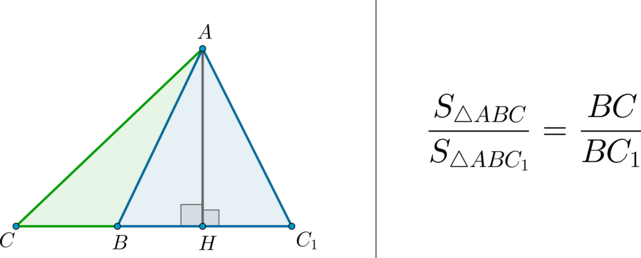
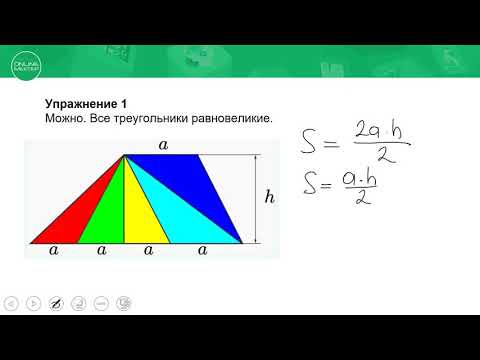
Можно заметить, что если сторону треугольника увеличить в k раз, а высоту, проведенную к этой стороне, уменьшить в k раз, то получим треугольник, равновеликий данному.
Равновеликие треугольники в треугольнике
Медиана делит треугольник на два равновеликих треугольника.
Равновеликие треугольники в трапеции
При пересечении диагоналей в произвольной трапеции ABCD образуется три пары равновеликих треугольников:
1) ∆ABD и ∆ACD,
1) Проведём в треугольниках ABD и ACD высоты BH и CF.
BK=CF (как высоты трапеции), следовательно,
3)
Так как площади треугольников ABD и ACD равны (по доказанному), то и
Таким образом, треугольники , образованные боковыми сторонами и диагоналями трапеции, имеют равные площади.
Видео:Равновеликие треугольникиСкачать
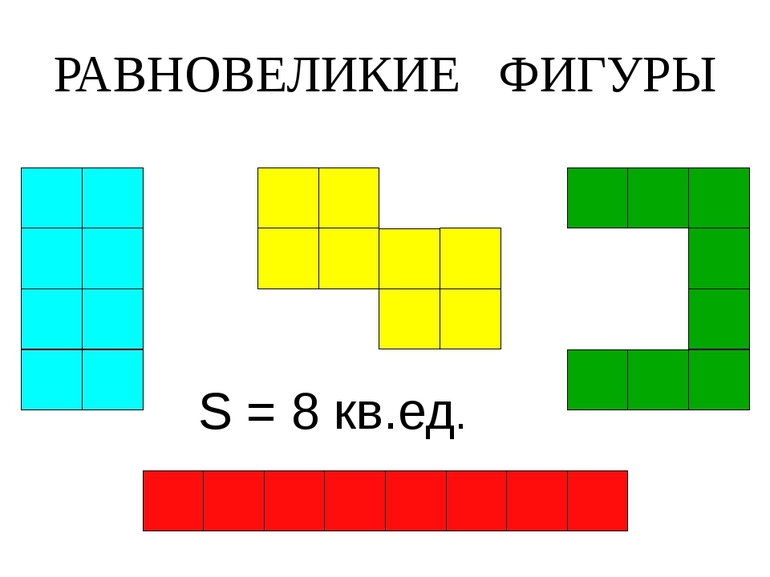
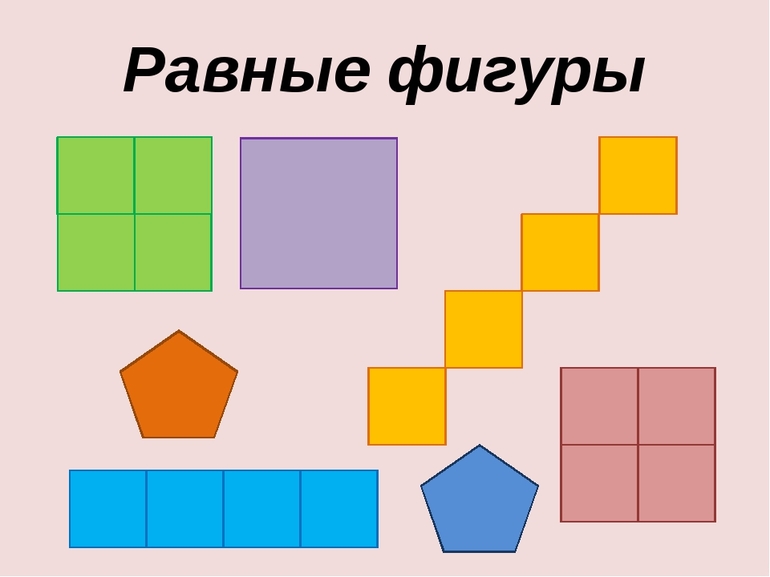
Равновеликие фигуры — свойства, формулы и примеры
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать
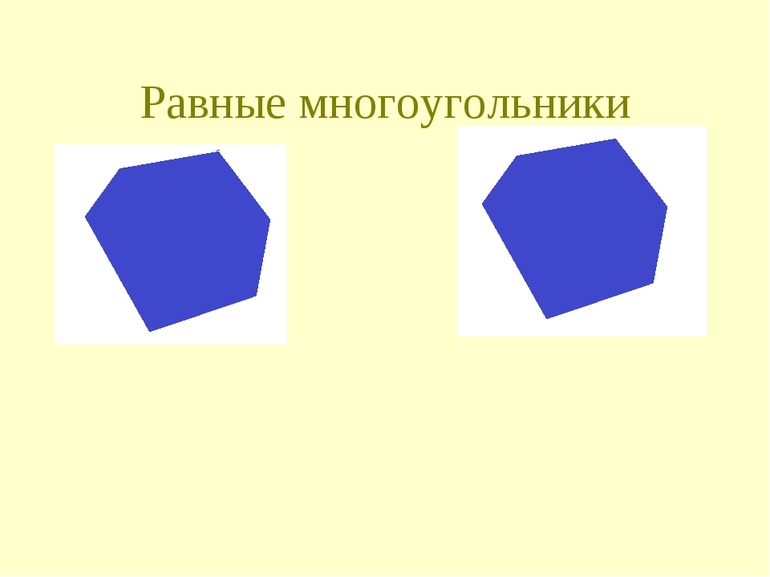
Равные многоугольники
По определению равные фигуры должны быть во всём одинаковыми, включая площадь, длину сторон, размер углов и другие параметры. Чтобы рассмотреть всё из них, уйдёт много времени, да это и не нужно, ведь они взаимозависимы. Хорошим примером будет самый простой многоугольник — треугольник. Существует несколько правил, по которым можно определить, равны ли 2 треугольника между собой или нет:
- По трём сторонам.
- По стороне и двум прилегающим к ней углам.
- По двум сторонам и углу между ними.
Нельзя путать первое условие с тремя углами. Ведь если в треугольнике равны 3 угла, они необязательно будут равными, но будут подобными.
Названия условий достаточно точно описывают критерии, по которым можно определить одинаковые 2 треугольника или нет. Из них следует, что необязательно знать все параметры: часто хватает только нескольких из них для определения «равности».
В большинстве случаев определить одинаковость других фигур гораздо сложнее, нежели треугольников. К счастью, чаще всего в школьной геометрии такой класс задач не рассматривают или даются дополнительные данные, помогающие с решением.
Например, доказательство «равности» для четырёхугольника сложнее, да и почти не встречается. Но если по условию сказано, что четырёхугольник не произвольный, а имеет прямые углы, задача становится проще. В таком случае рассматривается прямоугольник. А для него достаточно, чтобы 2 не противолежащие стороны были равны.
Если указано ещё и условие, что прямоугольник является квадратом, достаточно указать, что у двух таких фигур совпадает по длине одна сторона и уже этого будет достаточно.
Видео:Первый признак равенства треугольников. 7 класс.Скачать
Равность правильных фигур
Частным и самым простым для сравнения является случай, когда многоугольник по условию правильный. Так называется фигура с одинаковыми сторонами и углами. Например, равносторонний треугольник и квадрат. Важно не забывать проверить равны ли углы, так как не каждая фигура правильная. Тот же ромб по определению имеет 4 совпадающие по длине стороны, но разные углы. При сравнении правильных многоугольников достаточно указать, что, хотя бы одна сторона фигуры равна стороне у другой. Это будет достаточное условие для доказательства «равности».
Самым простым и наглядным способом сверки двух фигур будет не геометрический с помощью правил, а путём наложения рисунков друг на друга. Разумеется, что он не претендует на точность, но изобразить параллелограмм и наложить его на другой нагляднее, чем сравнивать, например, углы. Понятно, что так можно только ознакомиться с концепцией «равности» и показать, какие фигуры называются равными, для упрощения в дальнейшем решения задач, но доказывать что-либо нельзя, ввиду неточности метода.
Если при сравнении двух тел оказывается, что их площади равны, такие тела (многоугольники) являются равновеликими. Как и в случае с прошлым, это определение звучит несложно. Проблемы могут начаться непосредственно при вычислении площадей. Самый простой многоугольник — треугольник. Для вычисления его площади существует множество способов.
Видео:Признаки равенства треугольников. 7 класс.Скачать
Вычисление площади треугольника
Чаще всего приходится работать с прямоугольными треугольниками. Их площадь вычислить несложно — это полупроизведение катетов (сторон, между которыми лежит прямой угол). Таким образом, даже если стороны двух фигур по длине разные, но их произведение равно, они равновеликие. Например, треугольник с катетами 4 и 4 равен по площади многоугольнику с катетами 16 и 1. Так как их полупроизведение, а значит и площадь равна 8.
Если же треугольник произвольный (то есть не является частным случаем — прямоугольным, равнобедренным или равносторонним), можно воспользоваться одной из 5 формул, позволяющих вычислить его площадь.
- По двум сторонам и углу между ними.
- По стороне и высоте, проведённой к ней.
- По трём сторонам и полупериметру.
- По полупериметру и радиусу вписанной окружности.
- По трём сторонам и радиусу описанной окружности.
То, какую формулу использовать, будет зависеть от данных, предоставленных в задаче. Иногда придётся проводить дополнительное построение, например, провести высоту или использовать свойства, что биссектрисы пересекаются в центре вписанной окружности. Если не даны все 3 стороны, использовать третью формулу не получится.
Важно понять, что фигуры могут быть разными по количеству углов, но всё равно считаться равновеликими — в учёт идёт только площадь, остальные параметры не важны. Например, прямоугольный треугольник с катетами 2 и 4 будет визуально казаться больше, чем квадрат со стороной 2, но их площади совпадают и равны 4 (площадь прямоугольника считается как произведение прилежащих сторон друг на друга). По определению это делает их равновеликими.
Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать
Визуальный способ
Существует также наглядный, но неточный способ. Нужно взять листок в клеточку и нарисовать на нём многоугольники. Если рисунок получился большой — не страшно, так будет только проще в дальнейшем. Следующий шаг — посчитать количество клеток, которое заняла каждая фигура и сравнить. Если оно равно, равновеликость доказана. Опять же метод не точный, но для введения в концепцию площадей и их «равности» подойдёт.
Иногда встречается словосочетание «равносоставленная фигура». Такими называют произвольные многоугольники, которые можно составить друг из друга путём разрезания одного из них на одинаковые объекты и перекладывания. Например, если прямоугольник 4 на 1 нарезать на одинаковые части — квадраты 1 на 1, то из полученных маленьких квадратов можно составить один большой со стороной 2. Но это не более чем забавное свойство некоторых фигур и в геометрии фактически почти не используется.
Видео:8 класс, 22 урок, Первый признак подобия треугольниковСкачать
Основные свойства площадей треугольников
Факт 1.
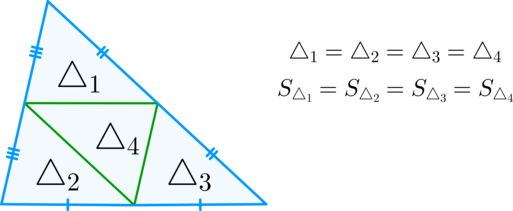
(bullet) Средние линии треугольника разбивают его на 4 равных треугольника.
Соответственно, площади этих треугольников равны.
Факт 2.
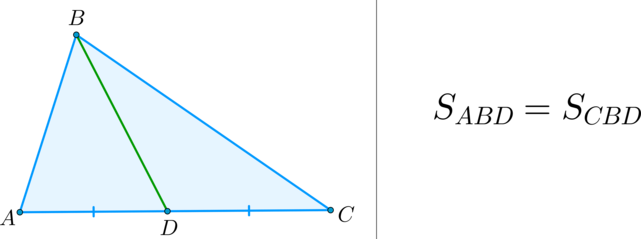
(bullet) Медиана треугольника делит его на два треугольника, равных по площади (равновеликих).
Факт 3.
(bullet) Все 3 медианы треугольника делят его на 6 равновеликих треугольников.
Факт 4.
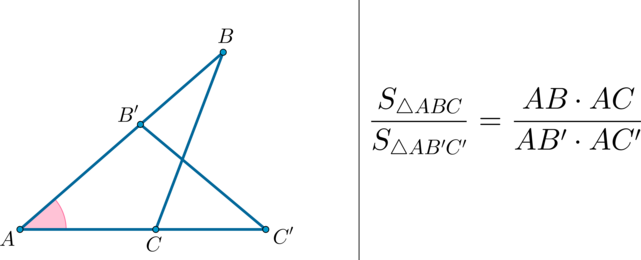
(bullet) Площади треугольников, имеющих одинаковый угол, относятся как произведения сторон, образующих этот угол.
Факт 5.
(bullet) Площади треугольников, имеющих одинаковое основание, относятся как высоты, проведенные к этим основаниям.
Факт 6.
(bullet) Площади треугольников, имеющих одинаковую высоту, относятся как основания, к которым проведена эта высота.
Факт 7.
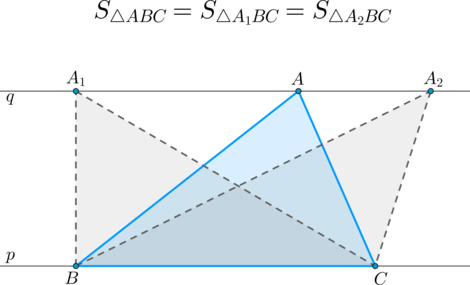
(bullet) Если прямые (p) и (q) параллельны, то 
Факт 8.
(bullet) Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
(bullet) Отношение периметров подобных треугольников равно коэффициенту подобия.
💥 Видео
Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать
✓ Свойства и признаки равнобедренного треугольника | Ботай со мной #008 | Борис ТрушинСкачать
Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать
Равновеликие треугольники. Треугольники с одинаковыми площадямиСкачать
7 класс, 15 урок, Первый признак равенства треугольниковСкачать
8 класс, 20 урок, Определение подобных треугольниковСкачать
8 класс. Геометрия. Равновеликость и равносоставленность фигур. 15.05.2020.Скачать
Геометрия 7. Урок 8 - Признаки равенства треугольников.Скачать
ТРИ ПРИЗНАКА РАВЕНСТВА ТРЕУГОЛЬНИКОВ НА ЕГЭ #shorts #математика #егэ #огэ #профильныйегэ #геометрияСкачать
Подобие прямоуголных треугольников. 1 признак.Скачать
Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать
Подобные треугольникиСкачать
Геометрия 8 класс (Урок№15 - Признаки подобия треугольников.)Скачать
