 Вписанные и центральные углы Вписанные и центральные углы |
 Углы, образованные хордами, касательными и секущими Углы, образованные хордами, касательными и секущими |
 Доказательства теорем об углах, связанных с окружностью Доказательства теорем об углах, связанных с окружностью |
- Вписанные и центральные углы
- Теоремы о вписанных и центральных углах
- Теоремы об углах, образованных хордами, касательными и секущими
- Доказательства теорем об углах, связанных с окружностью
- Центральные и вписанные углы
- Центральный угол и вписанный угол
- Свойства центральных и вписанных углов
- Примеры решения задач
- Центральные и вписанные углы — определение и вычисление с примерами решения
- Что такое вписанный угол
- Смежные и вертикальные углы
- Свойства углов, образованных при пересечении параллельных прямых секущей
- 🔥 Видео
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Вписанные и центральные углы
Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).
Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Видео:Углы, вписанные в окружность. 9 класс.Скачать

Теоремы о вписанных и центральных углах
| Фигура | Рисунок | Теорема | ||||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | |||||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же дугу равны. | ||||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды | ||||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды | ||||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр | ||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника |  |
| Вписанный угол | ||||||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника | ||||||||||||||||||||||||||||||||||||
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами |  |  | |
| Угол, образованный секущими, которые пересекаются вне круга |  |  | |
| Угол, образованный касательной и хордой, проходящей через точку касания |  |  | |
| Угол, образованный касательной и секущей |  |  | |
| Угол, образованный двумя касательными к окружности |  |  |
| Угол, образованный пересекающимися хордами хордами | |||
 | |||
Формула:  | |||
| Угол, образованный секущими секущими , которые пересекаются вне круга | |||
Формула:  | |||
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами | |||
| Угол, образованный касательной и хордой хордой , проходящей через точку касания | |||
 | |||
Формула:  | |||
| Угол, образованный касательной и секущей касательной и секущей | |||
Формула:  | |||
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами | |||
| Угол, образованный двумя касательными касательными к окружности | |||
Формулы:  | |||
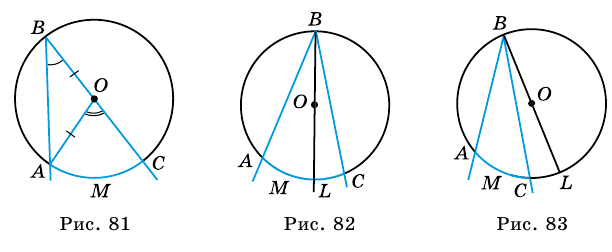
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать  Доказательства теорем об углах, связанных с окружностьюТеорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5). Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана. Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6). В этом случае справедливы равенства и теорема 1 в этом случае доказана. Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7). В этом случае справедливы равенства что и завершает доказательство теоремы 1. Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 8. Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 9. Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. Доказательство . Рассмотрим рисунок 10. Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства что и требовалось доказать Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 11. Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства что и требовалось доказать. Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 12. Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство Видео:ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ . §9 геометрия 8 классСкачать  Центральные и вписанные углыО чем эта статья: Видео:Центральные и вписанные углы. 16 задание ОГЭ 2022. 6 задание ЕГЭСкачать  Центральный угол и вписанный уголОкружность — замкнутая линия, все точки которой равноудалены от ее центра. Определение центрального угла: Центральный угол — это угол, вершина которого лежит в центре окружности. На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF Определение вписанного угла: Вписанный угол — это угол, вершина которого лежит на окружности. Вписанный угол равен половине дуги, на которую опирается. На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC Видео:ВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный УголСкачать  Свойства центральных и вписанных угловУглы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.
Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.
ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.
ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ. Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так: На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла. Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство. Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart! Хорда — отрезок, соединяющий две точки на окружности.
AB * AC = AE * AD
ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.
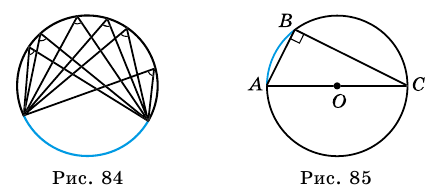
ㄥBAC + ㄥBDC = 180° Видео:8 класс, 34 урок, Теорема о вписанном углеСкачать  Примеры решения задачЦентральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно. Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ? Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80° Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла. Мы уже потренировались и знаем, как найти вписанный угол. Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности? СB = ⅕ от 360° = 72° Видео:7 класс, 11 урок, Смежные и вертикальные углыСкачать  Центральные и вписанные углы — определение и вычисление с примерами решенияСодержание: Центральным углом называют угол с вершиной в центре окружности. На рисунке 79 Если центральный угол больше развернутого, то соответствующая ему дуга больше полуокружности. Развернутому углу соответствует дуга, являющаяся полуокружностью. Дугу обозначают символом Дугу окружности можно измерять в градусах. Градусной мерой дуги окружности называют градусную меру соответствующего ей центрального угла. Например, если Очевидно, что градусная мера дуги, являющаяся полуокружностью, равна 180°, а дуги, являющейся окружностью, — 360°. На рисунке 79: Видео:ЕГЭ Задание 16 Свойство секущихСкачать  Что такое вписанный уголВписанным углом называют угол, вершина которого лежит на окружности, а стороны пересекают эту окружность. На рисунке 80 стороны вписанного угла Очевидно, что точки пересечения сторон вписанного угла с окружностью делят ее на две дуги. Той, на которую опирается вписанный угол, будет дуга, не содержащая его вершину. Например, на рисунке 80 стороны вписанного угла Теорема (о вписанном угле). Вписанный угол измеряется половиной дуги, на которую он опирается. Доказательство: Пусть Докажем, что 1) Пусть центр окружности — точка Следовательно, Но 2) Пусть центр окружности лежит внутри вписанного угла (рис. 82). Проведем луч Тогда 3) Пусть центр окружности лежит вне вписанного угла (рис. 83). Тогда Следствие 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны (рис. 84). Следствие 2. Вписанный угол, опирающийся на диаметр, — прямой (рис. 85). Пример: Докажите, что угол с вершиной внутри круга измеряется полусуммой двух дуг окружности, одна из которых лежит между сторонами угла, а вторая — между их продолжениями. Доказательство: Рассмотрим
Пример: Докажите, что угол между двумя секущими, пересекающимися вне круга, измеряется полуразностью большей и меньшей дуг окружности, лежащих между его сторонами. Доказательство: Рассмотрим Поэтому Доказательство теоремы о вписанном угле встречается в «Началах» Евклида. Но еще раньше этот факт, как предположение, впервые высказал Гиппократ Хиосский (V в. до н. э.). О том, что вписанный угол, опирающийся на диаметр, является прямым, было известно вавилонянам 4000 лет тому назад, а первое доказательство этого факта приписывают Фалесу Милетскому. Смежные и вертикальные углыДва угла называют смежными, если одна сторона у них общая, а две другие являются дополняющими лучами. На рисунке 262 углы Свойство смежных углов. Сумма смежных углов равна 180°. Два угла называют вертикальными, если стороны одного из них являются дополняющими лучами сторон другого. На рисунке 263 Свойство вертикальных углов. Вертикальные углы равны. Свойства углов, образованных при пересечении параллельных прямых секущей
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи Сайт пишется, поддерживается и управляется коллективом преподавателей Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC. Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг. 🔥 ВидеоУрок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать  №1 из ЕГЭ 2023 по математике. Лайфхаки для №16. Окружность, вписанные углы, хорды, касательныеСкачать  Геометрия. 8 класс. Урок 11 "Вписанные углы"Скачать  Вписанные и центральные углыСкачать  Углы между хордами, касательными и секущими | Геометрия 8-9 классыСкачать  Смежные и вертикальные углы. Практическая часть - решение задачи. 7 класс.Скачать  Центральные и вписанные углы - геометрия 8 классСкачать  Занятие 7. Окружность. Центральные и вписанные углы. Планиметрия для ЕГЭ и ОГЭСкачать  ОКРУЖНОСТИ, вписанные и описанные фигуры, углы // Занятие 3 // Готовимся к ОГЭ 2022 по математикеСкачать  Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать  |


















































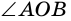
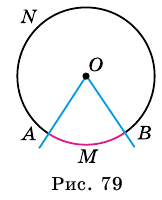
 который записывают перед названием дуги или над ним. Чтобы уточнить, о какой именно из двух дуг, на которые центральный угол разделил окружность, идет речь, на каждой из них отмечают произвольную точку, отличную от концов дуги. Например,
который записывают перед названием дуги или над ним. Чтобы уточнить, о какой именно из двух дуг, на которые центральный угол разделил окружность, идет речь, на каждой из них отмечают произвольную точку, отличную от концов дуги. Например, 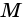 и
и 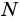 (рис. 79). Тогда эти дуги можно записать так:
(рис. 79). Тогда эти дуги можно записать так: 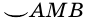 (или
(или 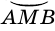 ) и
) и 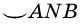 (или
(или 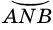 ). Если понятно, о какой именно дуге идет речь, то для ее обозначения достаточно указать лишь концы дуги, например
). Если понятно, о какой именно дуге идет речь, то для ее обозначения достаточно указать лишь концы дуги, например 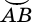 (или
(или 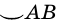 ).
).
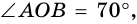 то
то 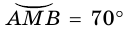 (рис. 79).
(рис. 79).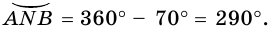
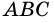 пересекают окружность в точках
пересекают окружность в точках 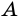 и
и 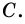 Говорят, что этот угол опирается на дугу
Говорят, что этот угол опирается на дугу 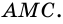
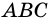 делят окружность на две дуги:
делят окружность на две дуги: 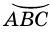 и
и 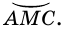 Так как
Так как 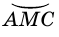 не содержит вершины угла (точки
не содержит вершины угла (точки 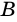 ), то является дугой, на которую опирается вписанный угол
), то является дугой, на которую опирается вписанный угол 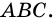 Эта дуга выделена цветом.
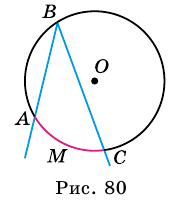
Эта дуга выделена цветом.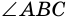 является вписанным в окружность с центром
является вписанным в окружность с центром 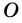 и опирается на дугу
и опирается на дугу 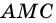 (рис. 80).
(рис. 80).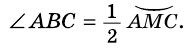 Рассмотрим три возможных положения центра окружности относительно вписанного угла.
Рассмотрим три возможных положения центра окружности относительно вписанного угла. — принадлежит одной из сторон угла, например
— принадлежит одной из сторон угла, например 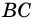 (рис. 81). Центральный угол
(рис. 81). Центральный угол 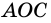 является внешним углом треугольника
является внешним углом треугольника 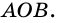 Тогда, по свойству внешнего угла,
Тогда, по свойству внешнего угла, 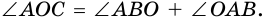 Но
Но 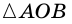 — равнобедренный (
— равнобедренный ( 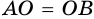 как радиусы), поэтому
как радиусы), поэтому 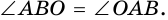
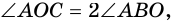 то есть
то есть 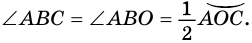
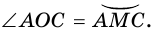 Таким образом,
Таким образом, 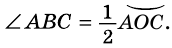
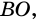 пересекающий окружность в точке
пересекающий окружность в точке 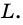
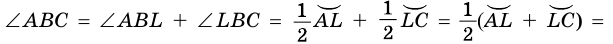
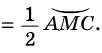
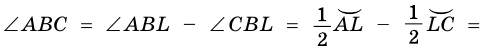
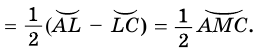
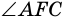 с вершиной внутри круга (рис. 86). Докажем, что
с вершиной внутри круга (рис. 86). Докажем, что 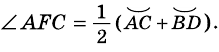
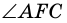 — внешний угол треугольника
— внешний угол треугольника 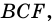 поэтому:
поэтому: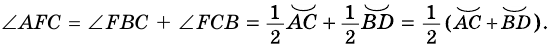
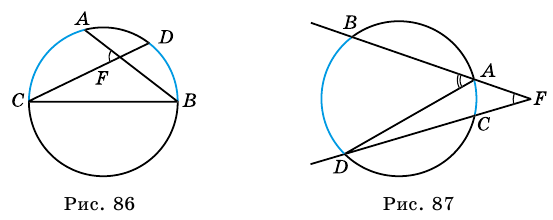
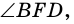 вершина которого лежит вне круга, a
вершина которого лежит вне круга, a 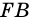 и
и 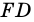 — секущие (рис. 87). Докажем, что
— секущие (рис. 87). Докажем, что 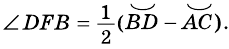
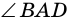 — внешний угол треугольника
— внешний угол треугольника 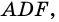 поэтому:
поэтому: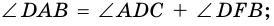 то есть
то есть 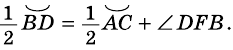
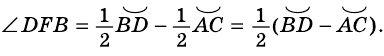
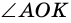 и
и 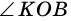 — смежные.
— смежные.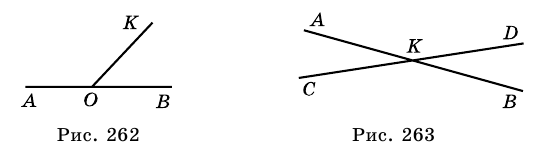
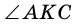 и
и 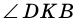 — вертикальные, углы
— вертикальные, углы 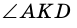 и
и 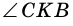 также вертикальные.
также вертикальные.