Верно ли что проекции параллельных прямых параллельны или совпадают (2 видео)

Верно ли что проекции параллельных прямых параллельны или совпадают

В стереометрии изучаются пространственные фигуры, однако на чертеже они изображаются в виде плоских фигур. Каким же образом следует изображать пространственную фигуру на плоскости? Обычно в геометрии для этого используется параллельное проектирование.
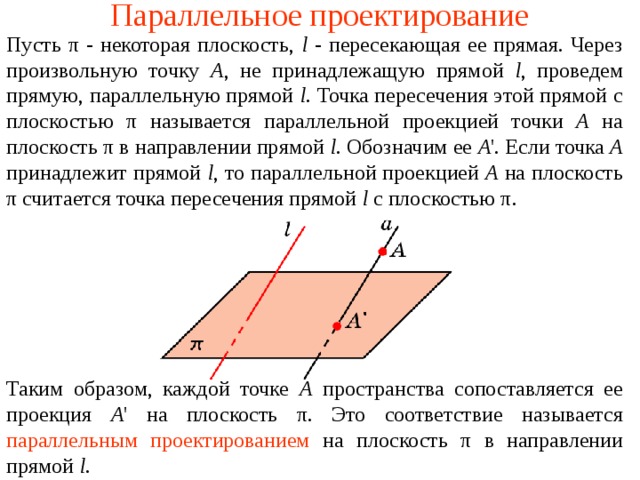
Пусть p — некоторая плоскость, l — пересекающая ее прямая (рис. 1). Через произвольную точку A, не принадлежащую прямой l, проведем прямую, параллельную прямой l. Точка пересечения этой прямой с плоскостью p называется параллельной проекцией точки A на плоскость p в направлении прямой l. Обозначим ее A‘. Если точка A принадлежит прямой l, то параллельной проекцией A на плоскость p считается точка пересечения прямой l с плоскостью p .

Таким образом, каждой точке A пространства сопоставляется ее проекция A‘ на плоскость p . Это соответствие называется параллельным проектированием на плоскость p в направлении прямой l .
Пусть Ф — некоторая фигура в пространстве. Проекции ее точек на плоскость p образуют фигуру Ф’, которая называется параллельной проекцией фигуры Ф на плоскость p в направлении прямой l. Говорят также, что фигура Ф’ получена из фигуры Ф параллельным проектированием.
Примеры параллельных проекций дают, например, тени предметов под воздействием пучка параллельных солнечных лучей.
Рассмотрим свойства параллельного проектирования.
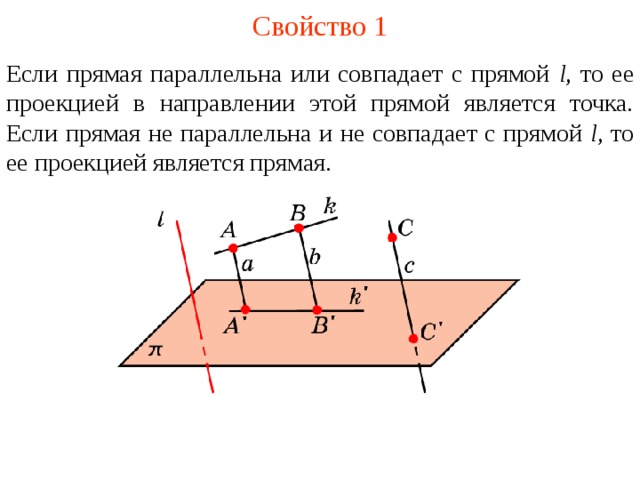
Свойство 1. Если прямая параллельна или совпадает с прямой l, то ее проекцией в направлении этой прямой является точка. Если прямая не параллельна и не совпадает с прямой l, то ее проекцией является прямая.
Доказательство. Ясно, что если прямая k параллельна или совпадает с прямой l, то ее проекцией в направлении этой прямой на плоскость p будет точка пересечения прямой l и плоскости p . Пусть k не параллельна и не совпадает с прямой l (рис. 2). Возьмем какую-нибудь точку A на прямой k и проведем через нее прямую a, параллельную l. Ее пересечение с плоскостью проектирования p даст точку A‘, являющуюся проекцией точки A. Через прямые a и k проведем плоскость a . Ее пересечением с плоскостью p будет искомая прямая k‘, являющаяся проекцией прямой k .

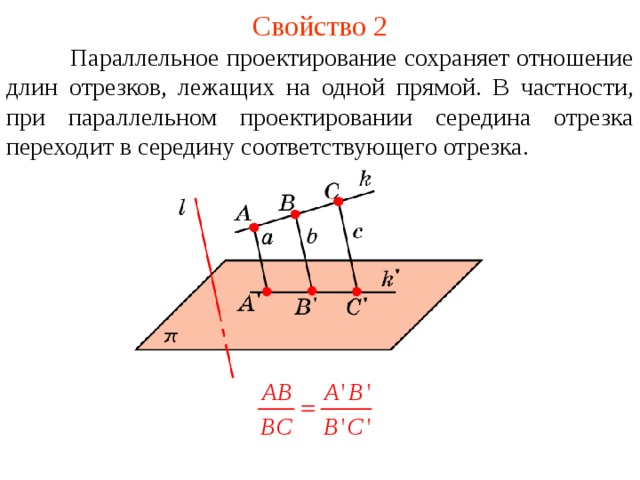
Свойство 2. Проекция отрезка при параллельном проектировании есть точка или отрезок, в зависимости от того лежит он на прямой, параллельной или совпадающей с прямой l, или нет. Параллельное проектирование сохраняет отношение длин отрезков, лежащих на прямой, не параллельной и не совпадающей с прямой l. В частности, при параллельном проектировании середина отрезка переходит в середину соответствующего отрезка.
Доказательство. Ясно, что если отрезок лежит на прямой, параллельной или совпадающей с прямой l, то его проекцией будет точка. Пусть точки A, B и C лежат на прямой k, не параллельной и не совпадающей с прямой l ; k’ – проекция прямой k на плоскость p в направлении прямой l ; A’, B’, C’ – проекции точек A, B и C соответственно; a, b, c – соответствующие прямые, проходящие через эти точки и параллельные прямой l (рис. 3). Тогда из теоремы Фалеса планиметрии следует равенство отношений AB : BC = A’B’ : B’C’. В частности, если точка B — середина отрезка AC , то B’ — середина отрезка A’C’ .
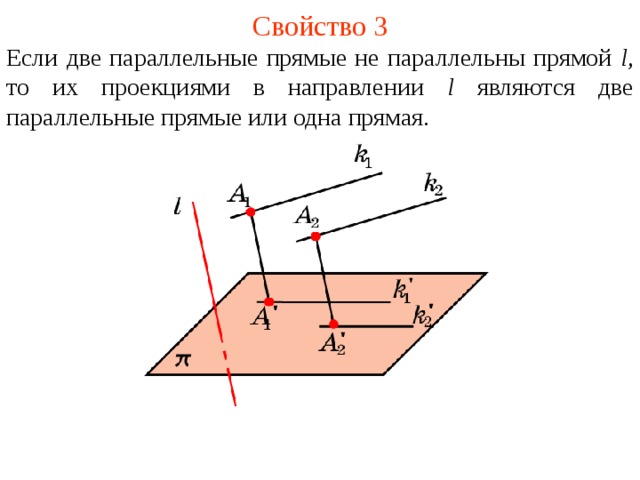
Свойство 3. Если две параллельные прямые не параллельны прямой l, то их проекции в направлении l могут быть или параллельными прямыми или одной прямой.
Доказательство. Пусть k ₁ , k ₂ — параллельные прямые, не параллельные прямой l. Так же как и при доказательстве первого свойства, рассмотрим плоскости a ₁ , a ₂ , линии пересечения которых с плоскостью p дают проекции k ₁‘ , k ₂‘ прямых k ₁ , k ₂ соответственно (рис. 4). Если плоскости a ₁ и a ₂ совпадают, то проекции прямых k ₁ и k ₂ также совпадают. Если эти плоскости различны, то они параллельны между собой, по признаку параллельности плоскостей (прямая k ₁ параллельна прямой k ₂ , прямая A ₁ A ₁‘ параллельна прямой A ₂ A ₂‘ ). В силу свойства параллельных плоскостей, линии пересечения этих плоскостей с плоскостью p параллельны.

При изображении пространственных фигур на плоскости особенно важно уметь правильно изображать плоские фигуры, поскольку они входят в поверхность основных пространственных фигур. Например, плоские многоугольники являются гранями многогранников, круги — основаниями цилиндров и конусов.
Теорема. Если плоская фигура F лежит в плоскости, параллельной плоскости проектирования p , то ее проекция F’ на эту плоскость будет равна фигуре F .
Доказательство. Пусть A , B – точки фигуры F и A ’ , B ’ – их параллельные проекции (рис. 5). Тогда ABB ’ A ’ – параллелограмм. Поэтому параллельный перенос на вектор переводит точку B в B ’ . Поскольку точку B фигуры F можно выбирать произвольно, то этот параллельный перенос переводит фигуру F в фигуру F ’ . Значит фигуры F и F ’ равны.

Если фигура F лежит в плоскости, не параллельной плоскости проектирования p , то ее проекция F’, вообще говоря, не равна фигуре F .
Из свойств параллельного проектирования следует, что параллельной проекцией многоугольника является или многоугольник с тем же числом сторон или отрезок. Причем, если в многоугольнике какие-нибудь две стороны параллельны, то их проекции также будут параллельны. Однако, поскольку при параллельном проектировании длины отрезков и углы, вообще говоря, не сохраняются, то проекцией равностороннего треугольника может быть треугольник с разной длиной сторон, проекцией прямоугольного треугольника может быть не прямоугольный треугольник. Аналогично, хотя проекцией параллелограмма является параллелограмм, проекцией прямоугольника может не быть прямоугольник, проекцией ромба не обязательно является ромб, проекцией правильного многоугольника может быть неправильный многоугольник.
Простейшим многоугольником является треугольник. Параллельной проекцией треугольника, как следует из свойств параллельного проектирования, является треугольник или отрезок. При этом, если плоскость треугольника параллельна плоскости проектирования, то, как мы выяснили, его проекцией будет треугольник, равный исходному. Докажем, что в общем случае треугольник любой формы может служить параллельной проекцией равностороннего треугольника.
Действительно, пусть дан произвольный треугольник ABC в плоскости p (рис. 6). Построим на одной из его сторон. например, AC равносторонний треугольник AB ₁ C так, чтобы точка B ₁ не принадлежала плоскости p . Обозначим через l прямую, проходящую через точки B ₁ и B. Тогда ясно, что треугольник ABC является параллельной проекцией треугольника AB ₁ C на плоскость p в направлении прямой l .

Рассмотрим теперь параллельную проекцию правильного шестиугольника ABCDEF с центром в точке O (рис. 7). Выберем какой-нибудь треугольник, например, AOB. Его проекцией может быть треугольник A’O’B’ на плоскости p (рис. 8), имеющий произвольную форму. Далее отложим O’D’=A’O’ и O’E’=B’O’. Теперь из точек A’ и D’ проведем прямые, параллельные прямой B’O’; из точек B’ и E’ проведем прямые, параллельные прямой A’O’. Точки пересечения соответствующих прямых обозначим F’ и C’. Шестиугольник A’B’C’D’E’F’ и будет искомой проекцией правильного шестиугольника ABCDEF .
Выясним, какая фигура является параллельной проекцией окружности. Пусть F — окружность в пространстве, F’— ее проекция на плоскость p в направлении прямой l. Если прямая l параллельна плоскости окружности или лежит в ней, то проекцией окружности является отрезок, равный диаметру окружности.
Рассмотрим случай, когда прямая l пересекает плоскость окружности (рис. 9). Пусть AB — диаметр окружности, параллельный плоскости p и A’B’ его проекция на эту плоскость. Тогда AB=A’B’. Возьмем какой-нибудь другой диаметр CD и пусть C’D’ — его проекция. Обозначим отношение C’D’ : CD через k. Так как при параллельном проектировании сохраняются параллельность и отношение длин параллельных отрезков, то для произвольной хорды C ₁ D ₁ , параллельной диаметру CD, ее проекция C ₁‘ D ₁‘ будет параллельна C’D’, и отношение C ₁‘ D ₁‘ : C ₁ D ₁ будет равно k .

Таким образом, проекция окружности получается сжатием или растяжением окружности в направлении какого-нибудь ее диаметра в одно и то же число раз. Такая фигура на плоскости называется эллипсом. Например, на рисунке 10 изображен эллипс, полученный из окружности сжатием в направлении диаметра CD в два раза.
Приведем примеры изображений пространственных фигур на плоскости.
Изображение параллелепипеда строится, исходя из того, что все его грани параллелограммы и, следовательно, изображаются параллелограммами (рис. 11).

При изображении куба плоскость изображений обычно выбирается параллельной одной из его граней. В этом случае две грани куба, параллельные плоскости изображений (передняя и задняя), изображаются равными квадратами. Остальные грани куба изображаются параллелограммами (рис. 12). Аналогичным образом изображается прямоугольный параллелепипед (рис. 13).
Для того чтобы построить изображение призмы, достаточно построить многоугольник, изображающий ее основание. Затем из вершин многоугольника провести прямые, параллельные некоторой фиксированной прямой, и отложить на них равные отрезки. Соединяя концы этих отрезков, получим многоугольник, являющийся изображением второго основания призмы (рис. 14).
Для того чтобы построить изображение пирамиды, достаточно построить многоугольник, изображающий ее основание. Затем выбрать какую-нибудь точку, которая будет изображать вершину пирамиды, и соединить ее с вершинами многоугольника (рис. 15). Полученные отрезки будут изображать боковые ребра пирамиды.

Для изображения цилиндра достаточно изобразить его основания в виде двух эллипсов, получающихся друг из друга параллельным переносом, и нарисовать две образующие, соединяющие соответствующие точки этих оснований (рис. 16).
Для изображения конуса достаточно изобразить его основание в виде эллипса, отметить вершину и провести через нее две образующие, являющиеся касательными к этому эллипсу (рис. 17).
Обратим внимание на тот факт, что плоское изображение, подчиняясь определенным законам, способно передать впечатление о трехмерном предмете. Однако при этом могут возникать иллюзии.
В живописи существует целое направление, которое называется импоссибилизм (impossibility — невозможность) — изображение невозможных фигур, парадоксов. Известный голландский художник М.Эшер (1898 – 1972) в гравюрах «Бельведер» (рис. 18), «Водопад» (рис. 19), «Поднимаясь и опускаясь» (рис. 20) изобразил невозможные объекты.

Современный шведский архитектор О. Рутерсвард посвятил невозможным объектам серию своих художественных работ. Некоторые из них представлены на рисунке 21.

Литература
1. Бескин Н.М. Изображение пространственных фигур //Квант. – 1970. — № 12.
2. Василевский А.Б. Метод параллельных проекций. – Минск: Народная асвета, 1985.
3. Костицын В.Н. Моделирование на уроках геометрии. – М.: Владос, 2000.
4. Польский И.Г. Проекционный чертеж и построения на нем. – М.: Учпедгиз, 1962.
5. Четверухин Н.Ф. Стереометрические задачи на проекционном чертеже. – 3-е изд. – М.: Учпедгиз, 1955.
6. Четверухин Н.Ф. Чертежи пространственных фигур в курсе геометрии. – М.: Учпедгиз, 1946.
7. Энциклопедия элементарной геометрии. Книга IV. Геометрия. – М.: Гос. изд. физико-математ. лит., 1963, с. 229.

Содержание

Параллельное проектирование
Просмотр содержимого документа «Параллельное проектирование»
Проекции параллельных прямых
📺 Видео

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Параллельное проектирование

Параллельное проектирование.10 класс Презентация составлена для изучения темы. Будет полезна учителям и учащимся.

Просмотр содержимого документа
«Параллельное проектирование»

Пусть π — некоторая плоскость, l — пересекающая ее прямая. Через произвольную точку A , не принадлежащую прямой l , проведем прямую, параллельную прямой l . Точка пересечения этой прямой с плоскостью π называется параллельной проекцией точки A на плоскость π в направлении прямой l . Обозначим ее A ‘. Если точка A принадлежит прямой l , то параллельной проекцией A на плоскость π считается точка пересечения прямой l с плоскостью π .

Таким образом, каждой точке A пространства сопоставляется ее проекция A ‘ на плоскость π . Это соответствие называется параллельным проектированием на плоскость π в направлении прямой l .

Если прямая параллельна или совпадает с прямой l , то ее проекцией в направлении этой прямой является точка. Если прямая не параллельна и не совпадает с прямой l , то ее проекцией является прямая.

Параллельное проектирование сохраняет отношение длин отрезков, лежащих на одной прямой . В частности, при параллельном проектировании середина отрезка переходит в середину соответствующего отрезка.

Если две параллельные прямые не параллельны прямой l , то их проекци ями в направлении l являются две параллельны е прямы е или одн а прям ая .

В каком случае параллельной проекцией прямой будет точка?

Ответ: Если прямая параллельна направлению проектирования.

Сколько точек может получиться при параллельном проектировании трех различных точек пространства?

Ответ: Три, или две, или одна.

Какие фигуры могут служить параллельными проекциями двух пересекающихся прямых?

Ответ: Две пересекающиеся прямые или одна прямая.

В каком случае параллельной проекцией двух параллельных прямых является одна прямая?

Ответ: Если они лежат в плоскости, параллельной направлению проектирования, но не параллельн ы ему.

В каком случае параллельной проекцией двух параллельных прямых являются две точки?

Ответ: Если они параллельны направлению проектирования.

Какие фигуры могут быть параллельными проекциями двух скрещивающихся прямых?

Ответ: Пересекающиеся прямые, параллельные прямые, прямая и точка.

Как должны быть расположены прямая и точка, чтобы они проектировались на плоскость в прямую и точку, принадлежащую этой прямой?

Ответ: Прямая не параллельна направлению проектирования, и через эту прямую и данную точку проходит плоскость, параллельная направлению проектирования.

Как должны быть расположены две прямые, чтобы они проектировались на плоскость в прямую и точку, принадлежащую этой прямой?

Ответ: Пересекат ь ся и одна из них параллельна направлению проектирования.

Как должны быть расположены две прямые, чтобы они проектировались на плоскость в прямую и точку, не принадлежащую этой прямой?

Ответ: Скрещиват ь ся и одна из них параллельна направлению проектирования.

Сохраняются ли при параллельном проектировании величины углов?

Сохраняются ли при параллельном проектировании длины отрезков?

Может ли параллельная проекци я угла быть больше (меньше) самого угла ?

Может ли параллельная проекци я отрезка быть больше (меньше) самого отрезка?

Верно ли, что если длина отрезка равна длине его параллельной проекции, то отрезок параллелен плоскости проектирования?

Точки A ’, B ’ являются параллельными проекциями точек A , B . AA ’ = a , BB ’ = b . Точка C делит отрезок AB в отношении m : n . Найдите расстояние между точкой C и ее проекцией C ’.

Решение. Через точку A проведем прямую AB” , параллельную A’B’ . Треугольник ACC” подобен треугольнику ABB”. Коэффициент подобия равен m 🙁 n+m ). Так как BB” = b – a , то CC”= ( b-a ) m 🙁 n+m ).

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Проекции параллельных прямых

Если прямые в пространстве параллельны, то их проекции также параллельны (рис. 5). Доказательство: прямые АВ и CD проецируются с помощью проецирующих плоскостей У и Т, но У¦Т, т. к. АВ¦CD по условию и ААN¦ССN — по построению. Известно, что если две параллельные плоскости пересекаются третьей, то образуются параллельные прямые. Здесь две параллельные плоскости У и Т пересекаются плоскостью проекций ПN и образуются параллельные прямые (АNВN¦CNDN).

Проекции геометрических фигур, параллельных плоскости проекций. Если данная геометрическая фигура — прямая, кривая линия или плоская фигура (треугольник, многоугольник, эллипс, окружность и т. п.) лежит в плоскости, параллельной плоскости проекций, то она проецируется на плоскость проекций в натуральную величину. Доказательство: дано У¦ПN и АВ У (рис. 6). Требуется доказать, что АВ¦АNВN и АВ=АNВN. Так как У¦ПN , то отрезки ААN и ВВN равны и параллельны. Следовательно, четырехугольник АВВNАN является параллелограммом и АВ¦АNВN, АВ=АNВN.

Так же доказывается теорема относительно любой плоской кривой и любой плоской фигуры.

— цилиндрические поверхности в параллельной системе проецирования и конические поверхности в центральной системе проецирования — проецируют пространственные кривые линии и пространственные фигуры.

Основное свойство проецирующей геометрической фигуры заключается в том, что точки, прямые или кривые линии, плоские и пространственные фигуры, расположенные на проецирующей геометрической фигуре, проецируются на линию пересечения этой фигуры с плоскостью проекций. Эта линия называется следом данной проецирующей геометрической фигуры или ее главной проекцией.

На рис. 7 показаны проецирующие геометрические фигуры в ортогональной системе проецирования: проецирующая прямая а, проецирующая плоскость У и проецирующая цилиндрическая поверхность Ф.

Прямая а, плоскость У и образующие цилиндрической поверхности Ф перпендикулярны плоскости проекций ПN . Их главные проекции аN , УN и ФN включают в себя проекции всех точек данной проецирующей геометрической фигуры.

Дополнения однокартинного чертежа. Ранее было показано, что одна проекция точки не определяет ее положения в пространстве.

Для того, чтобы чертеж был полным и обратимым, т.е. для того, чтобы по чертежу можно было представить положение точки в пространстве, применяются разные способы.

Способ числовых отметок. Около проекции точки ставится число, выражающее в некоторых линейных единицах расстояние данной точки от плоскости проекций.

На рис. 8 даны проекции различных геометрических фигур с числовыми отметками.

Около проекции точки А стоит цифра 20. Это означает, что точка А отстоит от плоскости проекций на расстоянии 20 линейных единиц.

Концы отрезка ВС отстоят от плоскости на расстояниях 15 и 30, вершины треугольника DEF — на расстояниях соответственно 0, 10 и 25.

Кривая поверхность задана кривыми линиями, принадлежащими поверхности и параллельными плоскости проекций (горизонталями, если плоскость ПN горизонтальна). Около каждой горизонтали стоит число, выражающее ее расстояние от плоскости ПN.

С помощью горизонталей изображается рельеф земной поверхности на топографических картах и сложные кривые поверхности, в том числе поверхности манекена и обувной колодки.

Проекции, полученные при центральном и параллельном проецировании, обладают рядом свойств.

Проекция точки есть точка. При заданном центре Р (.или направлении S) проецированию любой точки А пространства соответствует иа плоскости проекций п’ единственная точка А’. При этом проекция точки В, лежащей в плоскости проекций, совпадает с самой точкой (см. рис. 43).

Проекция прямой есть прямая. На рис. 46 лучи, проецирующие прямую т, создают плоскость S, которая пересекает плоскость проекций п’ по линии m’, являющейся проекцией на плоскость n’; S

т; S п п = т’. Проекция прямой определена, если известны проекции хотя бы двух ее точек (рис. 9). Если в пространстве прямая параллельна плоскости проекции п’, то ее проекция параллельна самой прямой (рис. 10). При этом при центральном проецировании проекции отрезков пропорциональны самим отрезкам, а при параллельном — равны им.

При параллельном проецировании сохраняется отношение величин отрезков прямой и их проекций (рис. 11):

При параллельном проецировании проекции параллельных прямых есть прямые параллельные (рис. 12). Если прямые т и п в пространстве параллельны, то и проецирующие их плоскости Sm и Sn тоже будут параллельны. При пересечении их с плоскостью проекций п’ получаем т’|| п’.

Проекцией плоскости является плоскость проекций. Плоскость состоит из бесконечного множества точек. При проецировании этого множества проецирующие лучи заполняют все пространство, а их точки пересечения с плоскостью проекций п’ — всю плоскость проекций.

Так как положение любой плоскости в пространстве определяется тремя ее точками, не лежащими на одной прямой, то проекция трех таких точек плоскости (рис. 13, а) устанавливает однозначное соответствие между проецирующей плоскостью и плоскостью проекций n’, которое позволяет определить проекции (рис. 13, б) любой точки D или прямой этой плоскости.

Если плоскость параллельна плоскости проекций, то проекции ее плоских фигур при центральном проецировании подобны самим фигурам (рис. 14, а), а при параллельном — равны им (рис. 14,6).

Если плоскость угла параллельна плоскости проекций, величина проекции угла и при центральном, и при параллельном проецировании равна натуральной величине. На рис. 54, a угол ABC = уголA’B’C’, так как АВС бесконечность А’В’С’, а на рис. 54, б угол ABC = углу А’В’С’, так как АВС = А’В’С’.

При параллельном проецировании проекции фигуры не изменяется при параллельном переносе плоскости j проекций (рис. 15).

Прямые и плоскости (поверхности) могут занимать в пространстве проецирующее положение, если с ними совпадают проецирующие лучи. При центральном проецировании это прямые и плоскости, проходящие через центр проекций, пирамидальные и конические поверхности, у которых вершины совпадают с центром проецирования (рис. 56). При параллельном проецировании — это прямые и плоскости, параллельные направлению проецирования, призматические и цилиндрические поверхности, ребра и образующие которых параллельны направлению проецирования (рис. 57).

Все эти геометрические фигуры можно рассматривать состоящими из проецирующих лучей, каждый из которых изображается точкой. Отсюда следует, что проекциями прямых, плоскостей, поверхностей, занимающих проецирующее положение, есть точки или линии их пересечения с плоскостью проекций («вырожденные» проекции).