Видео:Сечение сферыСкачать

Сечение сферы (шара) плоскостью
О сечении сферы плоскостью
Сечение сферы плоскостью есть окружность.
Пусть плоскость α пересекает сферу W(O,R). Из центра O опустим перпендикуляр OC на плоскость α.
Соединим произвольную точку M линии пересения плоскости α со сферой W(O,R) с точками O и C. Т.к. OC ⊥ α, то OC ⊥ CM.
В прямоугольном треугольнике ∆OCM CM 2 = OM 2 — OC 2 . Т.к. OM и OC — величины постоянные, то и CM — величина постоянная. Таким образом все точки линии пересечения плоскости α и сферы W(O,R) равноудалены от точки C, поэтому эта линия пересечения является окружностью с центром в точке C и радиусом r = CM.
Сечение шара плоскостью есть круг, а основание перпендикуляра проведенного из центра шара к пересекаемой плоскости есть центр круга, полученного в сечении.
Плоскость, проходящая через центр сферы (шара) называется диаметральной плоскостью.
Сечение сферы (шара) диаметральной плоскостью называется большой окружностью (большим кругом).
Статистика посещений | Номер ресурса в БелГИЭ: 137297 | Номер свидетельства в НИРУП «ИППС»: 4141816821
Видео:№8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать

Что такое шар (сфера): определение, свойства, формулы
В публикации мы рассмотрим определение и основные свойства шара и сферы, а также формулы, с помощью которых можно найти площадь поверхности и объем данных геометрических фигур.
Видео:Геометрия 11 класс (Урок№8 - Сфера и шар.)Скачать

Определение шара и сферы
Шар – это совокупность всех точек в трехмерном пространстве, которые находятся на расстоянии не больше заданного от точки, называемой центром шара (на рисунке ниже – это точка O). Другими словами, это совокупность точек, ограниченных сферой.
Шар образуется путем вращения круга вокруг своего диаметра (оси) на 180° или полукруга – на 360°.
Сфера – это поверхность шара. Образуется путем вращения окружности вокруг своего диаметра на 180° или полуокружности – на 360°.
Различают два вида шаров:
- замкнутый – включает сферу;
- открытый – исключает сферу.
Радиус шара (сферы) – расстояние между центром и точками, лежащими на его поверхности. На рисунке выше обозначен буквой R.
Диаметр шара (сферы) – отрезок, проходящий через центр шара и соединяющие две противоположные точки на его поверхности. Совпадает с осью шара, обычно обозначается буквой d.
Полюсы шара (сферы) – точки A и B, расположенные на концах его диаметра.
Видео:Сфера. Урок 9. Геометрия 11 классСкачать

Свойства шара и сферы
Свойство 1
Любое сечение шара плоскостью является кругом.
Свойство 2
Любое сечение сферы плоскостью является окружностью.
Свойство 3
Все точки сферы равноудалены от ее центра.
Свойство 4
Сфера имеет самый большой объем среди всех фигур в пространстве, имеющих одинаковую площадь поверхности.
Свойство 5
Через две любые диаметрально противоположные точки (максимально отдаленные друг от друга точки на окружности) можно провести неограниченное количество кругов для шара или окружностей для сфер радиусом, равным радиусу шара/сферы.
Примечание: если точки не диаметрально противоположны, то провести можно только один круг (окружность).
Видео:11 класс, 19 урок, Сфера и шарСкачать

Части шара
Сегмент шара – это часть шара, отсекаемая плоскостью. Иногда называется шаровым сегментом. На рисунке ниже окрашен в зеленый цвет.
Срез шара – часть шара между двумя параллельными плоскостями, пересекающими его. Также может называться шаровым слоем. На рисунке ниже закрашен желтым.
Сектор шара – состоит из шарового сегмента и конуса, вершина которого находится центре шара, а основание совпадает с основанием сегмента. На рисунке ниже сектор залит оранжевым.
Видео:Геометрия 11 класс: Сфера и шар. Уравнение сферы. Площадь сферыСкачать

Формулы для шара/сферы
В формулах ниже используется как радиус (R), так и диаметр фигур (d). Число π в расчетах обычно округляется до двух знаков после запятой и приблизительно равняется 3,14.
Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Урок геометрии в 11-м классе по теме «Шар и сфера. Сечение шара плоскостью»
Разделы: Математика
ТИП УРОКА: урок систематизации и обобщения знаний по данной теме.
ЦЕЛИ УРОКА (Слайд 2)
1. Образовательные:
- повторить определения сферы и шара и связанных с ними понятий (центр, радиус, диаметр, хорда, ось, диаметрально противоположные точки, большой круг, большая окружность);
- рассмотреть сечение шара плоскостью, удалённой от центра шара на расстоянии, меньшем радиуса шара
2. Развивающие:
- развивать пространственное воображение учащихся при решении геометрических задач, геометрическое мышление, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, память, внимание;
- учить учащихся учиться математике, самостоятельно добывать знания.
3. Воспитательные:
- воспитывать у учащихся ответственное отношение к учебному труду, волю;
- формировать эмоциональную культуру и культуру общения.
МЕТОДЫ ОБУЧЕНИЯ: словесный, наглядный, деятельностный.
ФОРМЫ ОБУЧЕНИЯ: коллективная, индивидуальная.
ОБОРУДОВАНИЕ: карточки с заданиями на каждый этап урока, оценочные листы учащихся, компьютер, проекционный экран, проектор
ХОД УРОКА
ОРГМОМЕНТ
Сегодня на уроке мы закрепим навыки решения задач по данной теме, рассмотрим сечения шара плоскостью, удаленной от центра шара на расстоянии, меньшем радиуса.
Наша цель-развитие пространственного воображения, геометрического мышления, грамотной математической речи.
ПРОВЕРКА ВЫПОЛНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ осуществляется до урока с целью уже на уроке акцентировать внимание всех обучающихся на возникших затруднениях.
УСТНАЯ РАБОТА (вопросы классу ): (Слайды 3-6)
1. Назовите формулу для нахождения высоты равностороннего треугольника со стороной а.
2. В каком отношении делится медиана точкой пересечения медиан треугольника?
3. Назовите формулу для вычисления:
а) площади произвольного треугольника;
б) площади прямоугольного треугольника.
4. Как найти высоту, опущенную на гипотенузу в прямоугольном треугольнике, зная длины катетов и гипотенузы? (Из какого равенства можно выразить высоту?)
5. Как записать формулу Герона для вычисления площади треугольника?
6. Как выразить расстояние от центра шара до секущей плоскости через радиус шара и радиус сечения? Показ соответствующих слайдов.
ОЦЕНОЧНЫЙ ЛИСТ ОБУЧАЮЩЕГОСЯ (Слайд 7)
Проводится инструктаж по заполнению листов.
| Задачи | Тестовая работа | Дополнительные задачи | Сумма баллов | Оценка | |||||||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 1 | 2 | 3 | ||
КРИТЕРИИ ОЦЕНИВАНИЯ: ПО 1 БАЛЛУ ЗА КАЖДОЕ ВЕРНО ВЫПОЛНЕННОЕ ЗАДАНИЕ;
- “5” — НЕ МЕНЕЕ 11 БАЛЛОВ;
- “4” — 9,10 БАЛЛОВ;
- “3” — МЕНЕЕ 9 БАЛЛОВ.
РЕШЕНИЕ ЗАДАЧ (Слайды 8,9)
1. Шар радиуса 2
2. Стороны треугольника 8см,15см и 17см. Найдите расстояние от плоскости треугольника до центра шара, касающегося всех сторон треугольника, если радиус шара равен 3 
3. Диагонали ромба 9см и 12см. Шаровая поверхность касается всех его сторон. Радиус шара 8,5см. Найдите расстояние от центра шара до плоскости ромба.
Желающий ученик приглашается для решения первой задачи за крылом доски. Учитель, проходя по рядам, отмечает в оценочных листах учащихся выполнение ими соответствующего задания. Затем проверка по решению на доске для тех, кто затрудняется. Аналогично проверяются остальные задачи. При необходимости учитель предлагает ребятам-консультантам оказать помощь нуждающимся.
ОТВЕТЫ: 1. 3см, 2. 6см, 3. 7,7см.
ВОПРОСЫ ДЛЯ ЗАКРЕПЛЕНИЯ (Слайд 10)
(задается по два-три вопроса, ученику, отвечающему у доски; при возникновении затруднений может помогать другой ученик):
- Что такое шар?
- Что такое шаровая поверхность или сфера?
- Что такое радиус, диаметр, хорда шара?
- Какие точки называются диаметрально противоположными?
- Что является сечением шара плоскостью, удалённой от центра шара на расстояние, меньшее радиуса шара?
- Какая плоскость называется диаметральной плоскостью шара?
- Что такое большой круг, большая окружность?
ТЕСТОВАЯ РАБОТА (Слайд 11)
Укажите верные ответы:
1. Все точки шара удалены от центра на расстояние, равное радиусу.
2. Центр сферы не принадлежит данной сфере.
3. Расстояние между любыми точками шара не больше диаметра.
4. Расстояние между любыми точками сферы не больше диаметра.
5. Всякое сечение сферы плоскостью есть окружность.
6. Всякое сечение шара плоскостью есть окружность.
7. Из двух сечений шара плоскостями больше площадь того, которое ближе к центру.
8. Радиус любого сечения сферы плоскостью не больше радиуса сферы.
1 2 3 4 5 6 7 8 н в в в в н в в
Ребята ставят в оценочных листах букву “В” при верном ответе или букву” Н” при неверном. После выполнения тестовой работы осуществляется проверка выполнения по ответам на слайде.
ДОМАШНЕЕ ЗАДАНИЕ (Слайд 13)
Даются комментарии учителя по выполнению домашнего задания (в рамках подготовки к контрольной работе).
1. Радиус шара 25см. Расстояние от центра шара до плоскости сечения равно 15см. Найдите: а) площадь сечения; б) длину окружности сечения.
2. Радиус шара равен 2
3. На расстоянии 2
ОТВЕТЫ: 1. 400 



Для желающих предлагается выполнить дома задачи 4-6 из карточки с дополнительным заданием на отдельную оценку. (Слайд 14)
ИТОГИ УРОКА (Слайд 19)
Учитель подводит итоги урока, задавая вопросы обучающимся по количеству набранных баллов. Просит сдать оценочные листы. Выставляются оценки в журнал и в дневник. Устное поощрение тех, кто успешно трудился на протяжении всего урока. Сбор листов успеха.
ЛИСТ УСПЕХА ОБУЧАЮЩЕГОСЯ
Рефлексия (Слайд 20)
| Вид работы | Устная работа | Решение задач | Тест | Дополнительное задание | Итог |
| Мнение ученика | |||||
| Примерные варианты ответов | Все ли понятно? | Было ли трудно? | Было ли интересно? | Можешь ли рассказать другим? | Итоговое мнение |
ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ (Слайд 17)
Те ребята, которые быстро справляются с предлагаемыми заданиями, получают карточки с задачами для дополнительного решения:
1. Найдите площадь сечения шара плоскостью, отстоящей от центра шара на 5см, если радиус шара равен 13см.
2. Радиус шара R образует с радиусом сечения шара плоскостью угол a. Найдите площадь сечения шара.
3. Точка В принадлежит окружности большого круга шара с центром О, а точка А принадлежит окружности с центром О1 сечения шара плоскостью. 
4. В треугольнике АВС 
5. Треугольник АВС вписан в окружность сечения шара плоскостью. АВ=ВС=40, АС=48, ОО1=5. Найдите радиус шара.
6. Треугольник АВС вписан в окружность сечения шара плоскостью. АВ=m, 
Найдите расстояние от центра шара радиуса R до плоскости сечения.
ОТВЕТЫ: 1. 144



Указание для решения задачи №5: (Слайд 15)
рассмотреть нахождение радиуса сечения шара плоскостью треугольника двумя способами:
а) используя подобие прямоугольных треугольников;
📽️ Видео
Сфера и шар. Сечение сферы. Вписанная и описанная сфераСкачать

Почему площадь сферы в четыре раза больше её тени? [3Blue1Brown]Скачать
![Почему площадь сферы в четыре раза больше её тени? [3Blue1Brown]](https://i.ytimg.com/vi/JsrRqLK8zKg/0.jpg)
Сфера и шарСкачать

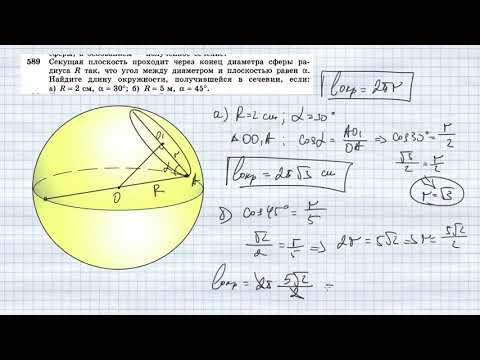
№589. Секущая плоскость проходит через конец диаметра сферы радиуса R так, что угол между диаметромСкачать
#33. СТЕРЕОМЕТРИЯ НА ЕГЭ — Задача о сфере!Скачать

Площадь сферыСкачать

11 класс, 22 урок, Касательная плоскость к сфереСкачать

11 класс, 21 урок, Взаимное расположение сферы и плоскостиСкачать

Сфера касается рёбер | Стереометрия | Физтех-2018. Математика | Борис Трушин |Скачать

Точка на поверхности сферы. Сечение сферы плоскостью.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

Плоские сечения сферыСкачать







