Верно или нет для точки лежащей на окружности (6 видео)

Верно или нет для точки лежащей на окружности

Какие из следующих утверждений верны?

1.Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу.

2.Площадь трапеции равна произведению основания трапеции на высоту.

3.Треугольника со сторонами 1, 2, 4 не существует.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Рассмотрим каждое из утверждений:

1.Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу — верно по определению

2.Площадь трапеции равна произведению основания трапеции на высоту — неверно, так как площадь трапеции равна произведению полусуммы оснований на высоту.

3.Треугольника со сторонами 1, 2, 4 не существует — верно, так как сумма двух сторон (1+2) меньше третьей стороны 4

Видео:№8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать

Верно или нет для точки лежащей на окружности

Задание 20. Какие из следующих утверждений верны?

1) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.

2) Площадь трапеции равна произведению основания трапеции на высоту.

3) Треугольника со сторонами 1, 2, 4 не существует.

1) Да, радиус – это и есть расстояние от центра окружности до любой точки, лежащей на окружности.

2) Нет, площадь трапеции равна полусумме оснований на высоту.

3) Да, если взять две стороны 1 и 2, то они при полной развертке (при 180 градусах) дадут длину в 3 единицы, поэтому третьей стороны в 4 единицы быть не может.

Видео:Через точку A, лежащую вне окружности, проведены две прямые.Скачать

Укажите номера верных утверждений. 4) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу

4) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.

5) Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.

6) Если радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 3, то эти окружности не имеют общих точек.

7) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются.

8) Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти окружности не имеют общих точек.

9) Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности пересекаются.

10) Точка пересечения двух окружностей равноудалена от центров этих окружностей.

11) Все диаметры окружности равны между собой.

30. Задание 10 № 311523. Точки A, B, C и D лежат на одной окружности так, что хорды AB и СD взаимно перпендикулярны, а ∠BDC = 25°. Найдите величину угла ACD.

Хорда пересекает диаметр окружности под углом 30° и делит его на отрезки длиной 4 см и 10 см. Найдите расстояние от центра окружности до этой хорды.

31. Задание 10 № 311912. В треугольнике ABC угол C равен 90°, AC = 30 , BC = Найдите радиус окружности, описанной около этого треугольника.

32. Задание 10 № 341673. Сторона AC треугольника ABC содержит центр описанной около него окружности. Найдите , если . Ответ дайте в градусах.

33. Задание 10 № 311410. Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей. Найдите длину хорды AC, если BD = 1 см, а радиус окружности равен 5 см.

34. Задание 10 № 324868. Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.

35. Задание 10 № 339623. Отрезки AB и CD являются хордами окружности. Найдите длину хордыCD, если AB = 20, а расстояния от центра окружности до хорд AB и CD равны соответственно 24 и 10.

36. Задание 15 № 27856. Найдите хорду, на которую опирается угол 90°, вписанный в окружность радиуса 1.

37. Задание 15 № 27858. Найдите хорду, на которую опирается угол , вписанный в окружность радиуса 3.

38. Задание 15 № 27862. Найдите хорду, на которую опирается угол , вписанный в окружность радиуса .

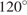
39. Задание 15 № 27867. Хорда делит окружность на две части, градусные величины которых относятся как 5:7. Под каким углом видна эта хорда из точки , принадлежащей меньшей дуге окружности? Ответ дайте в градусах.

40.

41. Задание 9 № 339502. Радиус окружности с центром в точке O равен 85, длина хорды AB равна 80 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.

42. Задание 17 № 311526. Обхват ствола секвойи равен 4,8 м. Чему равен его диаметр (в метрах)? Ответ округлите до десятых.

43. Задание 8 № 506308. Беговая дорожка стадиона имеет вид, показанный на рисунке, где ― длина каждого из прямолинейных участков, ― длина каждой из двух дуг. Сколько раз должен обежать стадион спортсмен, участвующий в забеге на 800 метров?