Векторная диаграмма цепи треугольник

Видео:Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Векторная диаграмма для трехфазной цепи

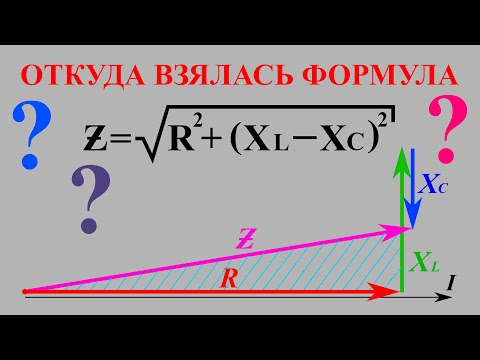
Цепь трехфазного тока может содержать в себе различные компоненты. Для ее стабильной работы, необходимо правильно рассчитать все напряжения, нагрузки и иные параметры. Статья даст подробное описание, что такое векторная диаграмма для трехфазной цепи, опишет ее разновидности, способы расчета.

Видео:Векторная диаграмма для трехфазной цепи │ТРЕУГОЛЬНИКСкачать

Определение

Векторной диаграммой называют метод графического изображения расчета всех параметров цепи переменного тока в виде векторов. Данный метод предполагает изображение всех составных напряжений, токов и процессов в виде отложенных векторов на плоскости.

Видео:Векторная диаграмма при соединении приемника треугольникомСкачать

Назначение

Векторная диаграмма используется для расчетов напряжений, токов в трехфазной цепи и других цепях переменного тока. Метод помогает определить значение всех процессов, происходящих в схеме, их влияние на каждый проводник, нейтраль, а также провести расчет возникающих нагрузок.

Видео:Векторная диаграммаСкачать

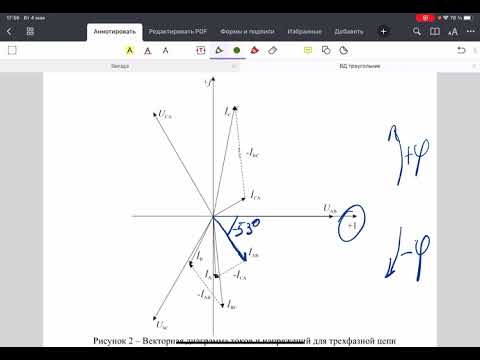
Разновидности

Векторные диаграммы трехфазных сетей могут быть симметричными или несимметричными. Построение гистограммы прямо зависит от ее схемы. Разновидности цепей и их гистограмм описаны далее в статье.

Видео:Несимметричная нагрузка. Схема соединения "треугольник"Скачать

Симметричные

Симметричные цепи переменного тока предполагают соединение 3 фаз от источника (генератора) с тремя приемниками.

При этом создаются совершенно независимые трехфазные схемы. При этом используется соединение трех фаз генератора звездой. Для симметричных схем должны соблюдаться требования:

1. Амплитуда должна быть для всех фаз одинаковой.
2. ЭДС должна иметь угол сдвига 120 градусов.
3. Угловые частоты должны быть равными.

Также учитывается принцип чередования ЭДС во времени. Если ротор генератора вращается по часовой стрелке (правое вращение), то происходит чередование прямого типа (A, B, C). Такая система считается симметричной.

Если ротор вращается против часовой стрелки (левое вращение), чередование считается обратным (A, C, B), но общая система ЭДС остается все так же симметричной.

Для симметричных схем применяется расчет по векторной гистограмме, приведенной ниже.

Видео:Векторные диаграммы и коэффициент мощностиСкачать

Несимметричные

Несимметричные цепи предполагают разницу сопротивлений на каждой фазе. Подобная разница может возникнуть при возникновении обрыва одного проводника или нейтрали, его плохого контакта, короткого замыкания. Например, при обрыве нейтрального провода возникает:

1. Увеличение сопротивления нейтрали.
2. Полное отсутствие проводимости.
3. Увеличение напряжения.
4. Максимальное искажение фазных напряжений.

При расчете несимметричной цепи также берется расчет соединения источника с приемниками по схеме звезда. Разница состоит в дополнительном расчете смещений, сдвигов фаз и величин сопротивления каждого проводника.

Ниже приведена векторная диаграмма несимметричной цепи.

Видео:Построение векторной диаграммы. Цепь RLCСкачать

Построение диаграммы

Векторная диаграмма предполагает в своей основе следующие значения:

1. Точку начала отсчета N для всех трех отдельных фаз.
2. Векторное направление ABC как отдельных проводников источника напряжения (генератора). Каждый вектор имеет заданную длину, равную своему напряжению.
3. Окончание векторов AВ, BС, CА, как приемников напряжения.

Данные значения дополняются единицей времени, за которое ток, под определенным напряжением и силой достигает приемников. Исходя из построения получаем результат: UAB=UBC=UCA.

А это значит то, что если фазная система напряжений симметрична, то линейная система также симметрична и равна, а кроме того имеет сдвиг на 120 градусов. Это простое определение вектора трехфазной цепи.

Переменный ток представляет собой синусоиду, которая может быть графически наложена на ось координат. При этом вектор имеет угловую скорость вращения, которая равна угловым частотам тока. При построении необходимо также учесть то, что вектор является графическим изображением амплитуды колебания, в котором угол колебания равен начальной точке отсчета.

Например, за ось координаты выбрано значение 0. Также известно значение угла смещения. Далее стоит провести вектор «Im», который определяет направление движения тока. При построении вектора с использованием этих значений станут видны параметры опережения, отставания или сдвига фазы. Таким образом можно визуально увидеть разницу величин на каждом проводнике схемы.

Видео:Векторная диаграмма токов и топографическая диаграмма напряженийСкачать

Заключение

Если вы работаете с трехфазными цепями, то векторная диаграмма используется для получения визуального отображения всех действующих процессов в таких цепях переменного трехфазного тока. Такая диаграмма полезна при определении несоответствий схемы между углами сдвига фаз, напряжениями и токами.

Видео:7. Решение задачи на трехфазные цепи по схеме треугольника.Скачать

Видео по теме

Видео:Как построить векторную диаграмму напряжений?Скачать

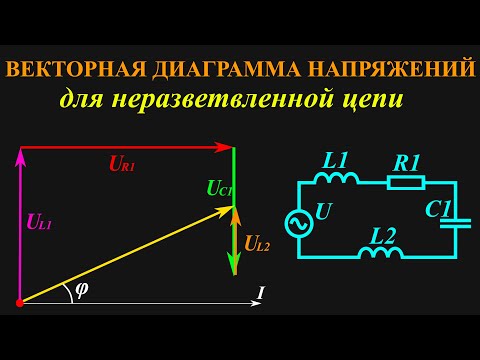
Соединение приемников энергии треугольником

При соединении приемников энергии треугольником (рис. 6-11) каждая фаза приемника присоединяется к линейным проводам, т. е. включается на линейное напряжение, которое одновременно будет и фазным напряжением приемника:

Таким образом, изменение сопротивления фаз не влияет на фазные напряжения.

Направления линейных токов от генератора к приемнику примем за положительные (рис. 6-11). Направления фазных токов от А’ к В’, от В’ к С‘ и от С’ к А’ также примем за положительные.

Согласно первому правилу Кирхгофа для мгновенных значений токов для узла А’ можно написать:

Аналогично для узла В’:

Рис. 6-11. Соединение приемников треугольником

Следовательно, мгновенное значение любого линейного тока равно алгебраической разности мгновенных значений токов тех фаз, которые соединены с данным проводом.

Рис. 6-12. Векторная диаграмма при соединении приемников треугольником.

Вектор любого линейного тока находится как разность векторов соответствующих фазных токов:

На рис. 6-12 дана векторная диаграмма для трехфазной цепи при соединении приемников энергии треугольником. На этой диаграмме все векторы проведены из одного начала. На рис. 6-13 дана вторая диаграмма для той же цепи, на которой векторы напряжений образуют треугольник, а вектор каждого фазного тока проведен из одного начала с вектором соответствующего фазного напряжения.

Рис. 6-13. Векторная диаграмма при соединении приемников треугольником.

Если при симметричной системе линейных напряжений нагрузка фаз равномерная, т. е.

то действующие значения фазных токов равны между собой и они сдвинуты по фазам на одинаковые углы от соответствующих напряжений (рис. 6-14) и, следовательно, на углы 120° один относительно другого. Следовательно, фазные токи представляют симметричную систему. Симметричную систему будут представлять и линейные токи (рис. 6-14).

Восстановив перпендикуляр из середины вектора линейного тока, например I_А, получим прямоугольный треугольник OHM, из которого следует, что

Таким образом, при соединении приемников треугольником при равномерной нагрузке фаз линейные токи больше фазных в √3 раз.

Кроме того, из той же векторной диаграммы следует, что линейные токи отстают от соответствующих фазных токов на углы 30°.

Рис. 6-14. Векторная диаграмма для цепи, соединенной треугольником при равномерной нагрузке фаз.

При соединении приемников треугольником при равно мерной нагрузке фаз расчет трехфазной цепи сводится к расчету одной фазы.

во фазного напряжения определяются из выражений

Активная мощность одной фазы

Реактивная мощность трех фаз

Полная мощность трехфазной цепи

При неравномерной нагрузке фаз мощность трехфазной цепи о пределяется как сумма мощностей отдельных фаз.

Если приемники энергии соединены звездой и за положительное направление линейных токов вобрано направление от генератора к потребителю, то согласно первому правилу Кирхгофа для нейтральной точки можно написать:

Если приемники энергии соединены треугольником, то сумма линейных токов

Следовательно, при любом способе соединения приемников алгебраическая сумма мгновенных значений линейных токов трехфазной трехпроводной цепи равна нулю.

Поэтому, например, намагничивающая сила трех жил трехфазного кабеля равна нулю и, следовательно, не происходит намагничивания стальной брони кабеля, применяемой для защиты от механических повреждений.

Видео:Как снять векторную диаграммуСкачать

ВКЛЮЧЕНИЕ ПРИЕМНИКОВ ЭНЕРГИИ В СЕТЬ ТРЕХФАЗНОГО ТОКА

Электрические лампы изготовляются на номинальные напряжения 127 и 220 в, а трехфазные электродвигатели на номинальные фазные напряжения 127, 220 и 380 в и выше.

Способ включения приемника в сеть трехфазного тока зависит от линейного напряжения сети и от номинального напряжения приемника.

Лампы с номинальным напряжением 127 в включаются треугольником при линейном напряжении сети 127 в и звездой с нейтральным проводом при линейном напряжений сета 220 в. Лампы с номинальным напряжением 220 в включаются треугольником в сеть с линейным напряжением 220 в и звездой с нейтральным проводом в сеть с линейным напряжением 380 в.

Трехфазный электродвигатель включается треугольником в сеть, линейное напряжение которой равно номинальному фазному напряжению электродвигателя. Если линейное напряжение сети превышает в √3 раз номинальное фазное напряжение электродвигателя, то он включается звездой.

Статья на тему Соединение приемников энергии треугольником

Похожие страницы:

Понравилась статья поделись ей

Leave a Comment

Для отправки комментария вам необходимо авторизоваться.

Видео:Векторная диаграмма - как она строится без чисел по схемеСкачать

Соединение потребителей электрической энергии в треугольник

При соединении фаз электроприемников в треугольник каждая фаза будет подключена к двум линейным проводам, как показано на рисунке ниже:

Поэтому при таком типе соединения, обратно звезде, независимо от характера и значения сопротивления приемника каждое фазное напряжение будет равно линейному, то есть U_Ф = U_Л. Если не брать во внимание сопротивления фазных проводов, то можно предположить, что напряжения источника и приемника электрической энергии равны.

На основании приведенной выше схемы и формулы можно сделать вывод, что соединение фаз приемников электрической энергии в треугольник следует применять тогда, когда каждая фаза трехфазного или двухфазного потребителя электрической энергии рассчитана на линейное напряжение сети.

В отличии от соединения звездой, где фазные и линейные токи равны, при соединении треугольником они равны не будут. Применив первый закон Кирхгофа к узловым точкам a, b, c получим соотношение между фазными и линейными токами:

Имея векторы фазных токов, используя данное соотношение, не трудно построить векторы линейных токов.

Видео:Зачем нужны векторные диаграммы?Скачать

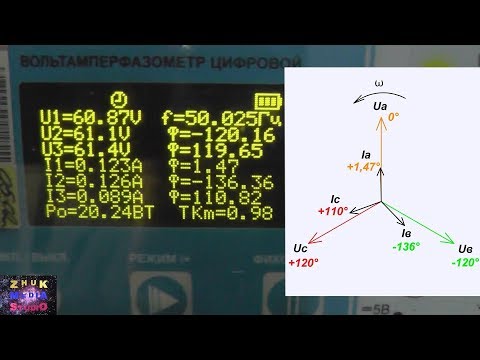
Симметричная нагрузка при соединении приемников треугольником

В отношении любой фазы можно применять формулы, которые справедливы для однофазных цепей:

Очевидно, что при симметричной нагрузке:

Векторная диаграмма фазных (линейных) напряжений и токов при активно-индуктивной симметричной нагрузке показана ниже:

В соответствии с формулой (1) были построены векторы линейных токов. Также стоит обратить внимание на то, что при построении векторных диаграмм для соединения треугольник вектор линейного напряжения U_ab принято направлять вертикально вверх.

Векторы линейных токов часто изображают соединяющими векторы фазных токов, как это показано на рисунке b):

На основании данной векторной диаграммы можно записать: . Такое же соотношение справедливо и для других фаз. Исходя из этого, можно вывести формулу зависимости между фазным и линейным током для соединения фаз потребителей треугольником при симметричной нагрузке .

Пример

Трехфазная сеть имеет линейное напряжение U_Л = 220 В. К ней необходимо подключить трехфазный электроприемник с фазным напряжением в 220 В и содержащим последовательно подключенные активное r_ф = 8,65 Ом и индуктивное x_ф = 5 Ом сопротивления.

Решение

Поскольку линейные и фазные напряжения в этом случае будут равны, то выбираем способ соединения обмоток потребителя в треугольник.

Линейные и фазные токи, а также полные сопротивления фаз будут равны:

Активная, реактивная и полная мощности электроприемника любой фазы будут равны:

Векторные диаграммы приведены выше.

Видео:Векторная диаграмма для трехфазной цепи. Звезда без нулевого проводаСкачать

Несимметричная нагрузка при соединении приемников треугольником

В случае несимметричного сопротивления фаз, как и при соединении в звезду, для подключения к сети электроприемники разбивают на три примерно одинаковые по мощности группы. Подключение каждой группы производится к двум фазным проводом, у которых есть отличия по фазе:

В пределах каждой группы подключение приемников производится параллельно.

После замены сопротивления нескольких приемников в одной фазе на одно эквивалентное получим такую схему:

Углы сдвига между напряжением и током, мощности и фазные токи можно найти из формулы (2). В случае несимметричной нагрузки (в нашем случае схема выше) фазные мощности, токи, а также углы сдвига (cos φ) не будут равны. Векторная диаграмма для случая, когда фаза ab имеет активную нагрузку, bc – активно-индуктивную, ca – активно-емкостную, показана ниже:

Для определения суммарной мощности всех фаз нужно применять выражение:

Пример

Дана несимметричная электрическая цепь, включенная по схеме выше, с параметрами: U_Л = 220 В, r_ab = 40 Ом, x_Lbc = 10 Ом, r_bс = 17,3 Ом, x_cа = 5 Ом, r_Ccа = 8,65 Ом. Нужно определить линейные и фазные токи, а также мощности.

Решение

Воспользовавшись выражением для определения комплексных значений получим:

Комплексные значения полных сопротивлений фаз: Z_ab = 40 Ом, Z_bс = 17,3 + j10 Ом, Z_bс = 8,65 – j5 Ом.

Комплексные и действующие значения линейных и фазных токов:

Дольше можно проводить расчеты, не прибегая к комплексному методу:

Общие активные и реактивные мощности:

Углы сдвига между токами и напряжениями:

Векторная диаграмма для несимметричного треугольника приводилась выше.

📹 Видео

Анализ не стандартной векторной диаграммы. часть 1Скачать

Векторная диаграмма при соединении приемника звездойСкачать

Расчет Трехфазной цепи Без комплексных чисел. Соединение треугольникомСкачать

Трехфазные цепи - ТРЕУГОЛЬНИК. Расчет трехфазной цепи, соединенной треугольникомСкачать

Откуда взялась формула полного сопротивления цепи? Треугольник напряжений, треугольник сопротивленийСкачать