В треугольнике четыре угла

Треугольники

Определение

Треугольник — это геометрическая фигура, которая состоит из
трех точек, не лежащих на одной прямой и трех отрезков,
соединяющих эти точки.

Точки называются вершинами треугольника.
Отрезки называются сторонами треугольника.

• три угла
• три вершины
• три стороны

Виды углов в треугольнике:

Чтобы лучше понять какие бывают треугольники узнаем
какие бывают углы в треугольниках.

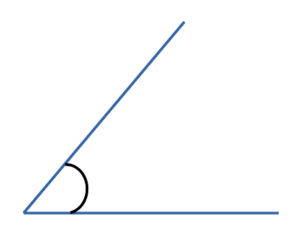
• Острый угол
  Это любой угол меньше 90°.

• Тупой угол
  Это любой угол больше 90°, но меньше 180°.

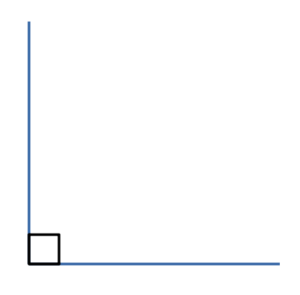
• Прямой угол
  Это угол 90°.

• Развернутый угол
  Это угол 180°.

Виды треугольников:

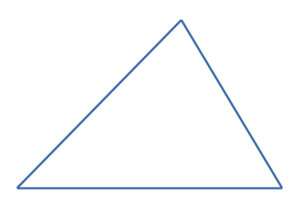
• Острый треугольник
  Это треугольник в котором все углы острые.

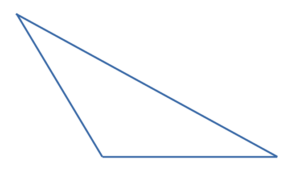
• Тупоугольный треугольник
  Это треугольник в котором один из углов тупой.

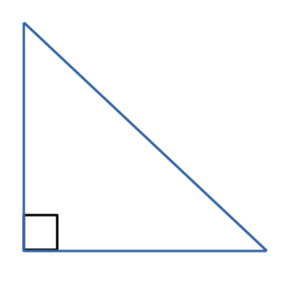
• Прямоугольный треугольник
  Это треугольник в котором один из углов прямой.

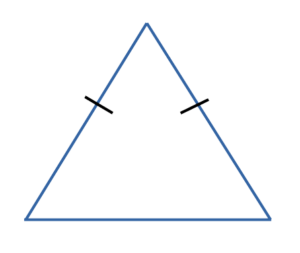
• Равнобедренный треугольник
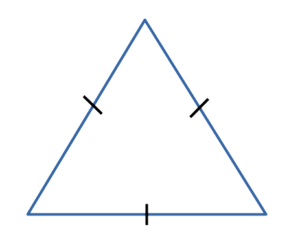
  Это треугольник в котором две боковые стороны равны.
  
• Равносторонний треугольник
  Это треугольник в котором все стороны равны.
  

Признаки равенства треугольников

С помощью признаков равенства треугольников можно
доказать что те или иные треугольники равны между собой.

math4school.ru

Треугольники

Основные свойства

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

Углами (внутренними углами) треугольника называются три угла, каждый из которых образован тремя лучами, выходящими из вершин треугольника и проходящими через две другие вершины.

Внешним углом треугольника называется угол, смежный внутреннему углы треугольника.

Сумма углов треугольника равна 180°:

Внешний угол равен сумме двух внутренних углов, не смежных с ним, и больше любого внутреннего, с ним не смежного:

Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон:

В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол:

Средней линией треугольника называется отрезок, который соединяет середины двух его сторон.

Средняя линия треугольника параллельна одной из его сторон и равна её половине:

Равенство треугольников

Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны:

У равных треугольников все соответствующие элементы равны (стороны, углы, высоты, медианы, биссектрисы, средние линии и т.д.)

В равных треугольниках против равных сторон лежат равные углы, а против равных углов – равные стороны.

Первый признак равенства треугольников.

Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны:

Второй признак равенства треугольников.

Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны:

Третий признак равенства треугольников.

Если три стороны одного треугольника равны соответственно трём сторонам другого треугольника, то такие треугольники равны:

Подобие треугольников

Подобными называются треугольники, у которых соответствующие стороны пропорциональны.

Коэффициент пропорциональности называется коэффициентом подобия:

Два треугольника подобны, если:

• Два угла одного треугольника равны двум углам другого треугольника.
• Две стороны одного треугольника пропорциональны двум сторонам другого, и углы, образованные этими сторонами, равны.
• Стороны одного треугольника пропорциональны сторонам другого.

У подобных треугольников соответствующие углы равны, а соответствующие отрезки пропорциональны:

Отношение периметров подобных треугольников равно коэффициенту подобия.

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Прямая, пересекающая две стороны треугольника, и параллельная третьей, отсекает треугольник, подобный данному:

Три средние линии треугольника делят его на четыре равных треугольника, подобные данному, с коэффициентом подобия ½:

Медианы треугольника

Медианой треугольника называется отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Три медианы треугольника пересекаются в одной точке, делящей медианы в отношении 2:1, считая от вершины:

• Медиана делит треугольник на два равновеликих (с равными площадями) треугольника.
• Три медианы треугольника делят его на шесть равновеликих треугольников:

Длины медиан, проведённых к соответствующим сторонам треугольника, равны:

Биссектрисы треугольника

Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне.

Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник.

Биссектриса внутреннего угла треугольника делит противолежащую углу сторону на отрезки, пропорциональные двум другим сторонам:

Длина биссектрисы угла А :

Биссектрисы внутреннего и смежного с ним внешнего угла перпендикулярны.

Биссектриса внешнего угла треугольника делит (внешне) противолежащую сторону на отрезки, пропорциональные двум другим сторонам.

BL – биссектриса угла В ;

ВЕ – биссектриса внешнего угла СВК :

Высоты треугольника

Высотой треугольника называется перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны.

Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.

Высоты треугольника обратно пропорциональны его сторонам:

Длина высоты, проведённой к стороне а :

Серединные перпендикуляры

Серединный перпендикуляр – это прямая, которая проходит через середину стороны треугольника перпендикулярно к ней.

Три серединных перпендикуляра треугольника пересекаются в одной точке, которая является центром окружности, описанной около данного треугольника.

Точка пересечения биссектрисы угла треугольника с серединным перпендикуляром противолежащей стороны лежит на окружности, описанной около данного треугольника.

Окружность, вписанная в треугольник

Окружность называется вписанной в треугольник, если она касается всех его сторон.

Точки касания вписанной окружности сторон треугольника отсекают от его сторон три пары равных между собой отрезков:

Радиус вписанной в треугольник окружности – расстояние от её центра до сторон треугольника:

Окружность, описанная около треугольника

Окружность называется описанной около треугольника, если она проходит через все его вершины.

Радиус описанной окружности:

Расположение центра описанной окружности

Центр описанной окружности остроугольного треугольника расположен внутри треугольника.Центр описанной окружности прямоугольного треугольника совпадает с серединой его гипотенузы.Центр описанной окружности тупоугольного треугольника расположен вне треугольника.

Равнобедренный треугольник

Треугольник называется равнобедренным, если у него две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.

В равнобедренном треугольнике углы при основании равны: ∠ A = ∠ C.

В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой, и высотой: BL – медиана, биссектриса, высота.

Основные формулы для равнобедренного треугольника:

Равносторонний треугольник

Треугольник у которого все стороны равны называется равносторонним или правильным треугольником.

Центры вписанной и описанной окружностей правильного треугольника совпадают.

Все углы равностороннего треугольника равны:

Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой, которые проведены из той же вершины:

Основные соотношения для элементов равностороннего треугольника

Прямоугольный треугольник

Треугольник называется прямоугольным, если у него есть прямой угол.

Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.

Прямоугольные треугольники равны если у них равны:

• два катета;
• катет и гипотенуза;
• катет и прилежащий острый угол;
• катет и противолежащий острый угол;
• гипотенуза и острый угол.

• одному острому углу;
• из пропорциональности двух катетов;
• из пропорциональности катета и гипотенузы.

Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу:

Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу:

Высота прямоугольного треугольника, проведённая из вершины прямого угла, может быть определена через катеты и их проекции на гипотенузу:

Медиана, проведённая из вершины прямого угла, равна половине гипотенузы:

Высота прямоугольного треугольника, проведённая из вершины прямого угла, делит данный треугольник на два треугольника, подобные данному:

Площадь прямоугольного треугольника можно определить

через катеты:

через катет и острый угол:

через гипотенузу и острый угол:

Центр описанной окружности совпадает с серединой гипотенузы.

Радиус описанной окружности:

Радиус вписанной окружности:

Вневписанные окружности

Три окружности, каждая из которых касается одной стороны (снаружи) и продолжений двух других сторон треугольника, называются вневписанными.

Центр вневписанной окружности лежит не пересечении биссектрисы одного внутреннего угла и биссектрис внешних углов при двух других вершинах.

Так точка О₁ , центр одной из вневписанных окружностей Δ ABC , лежит на пересечении биссектрисы ∠ A треугольника ABC и биссектрис BО₁ и C О₁ внешних углов Δ ABC при вершинах B и C .

Таким образом, шесть биссектрис треугольника – три внутренние и три внешние – пересекаются по три в четырёх точках – центрах вписанной и трёх вневписанных окружностей.

Δ ABC является ортоцентричным в Δ О₁О₂О₃ (точки A , B и C – основания высот в Δ О₁О₂О₃ ).

В Δ ABC углы равны 180°–2 О₁ , 180°–2 О₂ , 180°–2 О₃ .

Радиус окружности, описанной около Δ О₁О₂О₃ , равен 2 R , где R – радиус окружности, описанной около Δ ABC .

Δ ABC имеет наименьший периметр среди всех треугольников, вписанных в Δ О₁О₂О₃ .

Если r_a , r_b , r_с – радиусы вневписанных окружностей в Δ ABC , то в Δ ABC верно:

для r –

для R –

для S –

для самих r_a , r_b , r_с –

Теоремы синусов, косинусов, тангенсов; формулы Мольвейде

Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними:

• если c 2 > a 2 +b 2 , то угол γ – тупой ( cos γ
• если c 2 2 +b 2 , то угол γ – острый ( cos γ > 0 );
• если c 2 = a 2 +b 2 , то угол γ – прямой ( cos γ = 0 ).

Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Коэффициент пропорциональности равен диаметру описанной окружности:

Теорема тангенсов (формула Региомонтана):

Геометрия. Урок 3. Треугольники

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Определение треугольника

• Виды треугольников

• Отрезки в треугольнике

Определение треугольника

Треугольник – многоугольник с тремя сторонами и тремя углами.

Угол ∠ A – угол, образованный сторонами A B и A C и противолежащий стороне B C .

Угол ∠ B – угол, образованный сторонами B A и B C и противолежащий стороне A C .

Угол ∠ C – угол, образованный сторонами C B и C A и противолежащий стороне A B .

Виды треугольников

Треугольник остроугольный , если все три угла в треугольнике острые.

Треугольник прямоугольный , если у него один из углов прямой ( = 90 ° ) .

Треугольник тупоугольный , если у него один из углов тупой.

Основные свойства треугольника:

• Против большей стороны лежит больший угол.
• Против равных сторон лежат равные углы.
• Сумма углов в треугольнике равна 180 ° .
• Если продолжить одну из сторон треугольника, например, A C , и взять на продолжении стороны точку D , образуется внешний угол ∠ B C D к исходному углу ∠ A C B .

Отрезки в треугольнике

Биссектриса угла – луч, выходящий из вершины угла и делящий его пополам.

Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне.

Свойства биссектрис треугольника:

• Биссектриса угла – геометрическое место точек, равноудаленных от сторон угла.
• Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам:

Замечание: биссектриса угла – это луч, а биссектриса треугольника – отрезок.

Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

Свойства медиан треугольника:

• Медиана разбивает треугольник на два равновеликих треугольника (два треугольника, имеющих одинаковую площадь).
• Медианы треугольника пересекаются в одной точке. Точка пересечения медиан делит их в отношении 2:1, считая от вершины.

Высота треугольника – это перпендикуляр, проведенный из вершины угла треугольника к прямой, содержащей противолежащую сторону этого треугольника.

Если треугольник остроугольный, то все три высоты будут лежать внутри треугольника. Если треугольник тупоугольный, то высоты, проведенные из вершин острых углов будут лежать вне треугольника, а высота, проведенная из вершины тупого угла будет лежать внутри треугольника.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Свойство средней линии треугольника: средняя линия параллельна одной из его сторон и равна половине этой стороны.

Всего в треугольнике можно провести три средние линии. Три средние линии разбивают исходный треугольник на четыре равных треугольника. Площадь каждого маленького треугольника будет равна четверти площади большого треугольника.

Площадь треугольника

Площадь произвольного треугольника можно найти следующими способами:

Полупроизведение стороны на высоту, проведенную к этой стороне.

Равнобедренный треугольник

Равнобедренным называется треугольник, у которого две стороны равны.

Равнобедренный треугольник может быть остроугольным, прямоугольным и тупоугольным.

Свойства равноберенного треугольника:

• В равнобедренном треугольнике углы при основании равны.
• В равнобедренном треугольнике медиана, высота и биссектриса, проведенные к основанию, совпадают.

Равносторонний треугольник

Равносторонним называется треугольник, у которого все стороны и все углы равны.

Площадь равностороннего треугольника находится по формуле S = a 2 3 4

Высота равностороннего треугольника находится по формуле h = a 3 2

Прямоугольный треугольник

Треугольник называется прямоугольным, если у него один из углов равен 90 ° .

Свойства прямоугольного треугольника:

• Сумма двух острых углов треугольника равна 90 ° .
• Катет, лежащий напротив угла в 30 ° , равен половине гипотенузы.
• Если катет равен половине гипотенузы, он лежит напротив угла в 30 ° .

Теорема Пифагора

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

У прямоугольного треугольника катеты перпендикулярны друг другу, следовательно, площадь можно найти по формуле:

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с треугольниками