Условие
В треугольник ABC вписана окружность, которая касается сторон AB,
BC и CA в точках P,Q и R
Найдите BQ, если AB=66 см, BC=115 см, CA=87 см.
Решение
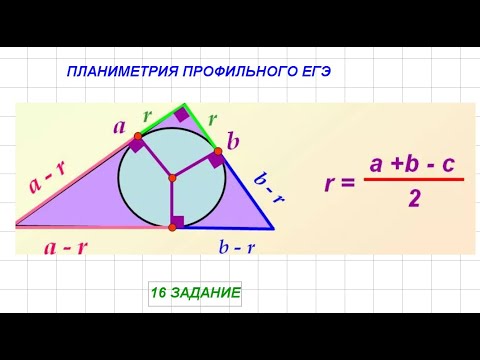
Cвойство касательной к окружности, проведенной из одной точки.
Отрезки касательных равны.
Обозначены на рисунке одинаковым цветом и одной переменной.
х+у=115
х+z=66
z+y=87
Система трех уравнений с тремя неизвестными.
Складываем все три уравнения
2х+2у+2z=268 ⇒
x+y+z=134
О т в е т. BQ=x=47 см
откуда получилось 134
Складываем все три уравнения 2х+2у+2z=268 делим на 2 ⇒ x+y+z=134
Видео:В треугольник АВС вписана окружность, которая касается АВ в точке РСкачать
В треугольник ABC вписана окружность, которая касается сторон AB, BC, AC соответственно в точках M, D, N. Найдите MD, если известно, что NA = 2, NC = 3,  BCA = 60 o .
BCA = 60 o .
Обозначим BM = BD = x. Тогда
По теореме косинусов
AB 2 = AC 2 + BC 2 — 2AC . BC cos
Из этого уравнения находим, что x = 5. Тогда AB = 7, BC = 8.
Еще раз применяя теорему косинусов к треугольнику ABC, находим, что
cos



Искомый отрезок MD находим по теореме косинусов из равнобедренного треугольника MBD:
MD = 



Ответ

Видео:№692. В треугольник ABC вписана окружность, которая касается сторон АВ, ВС и СА в точках Р, Q и RСкачать
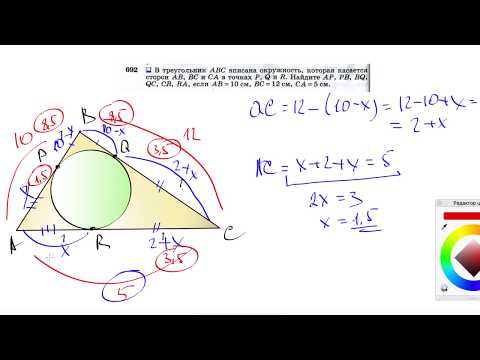
В треугольнике abc вписана окружность которая касается сторон ab
Окружность, вписанная в треугольник ABC, касается сторон AB, BC и CA в точках K, M и N соответственно.
а) Докажите, что
б) Найдите отношение AK : KB, если известно, что AN : NC = 4 : 3 и
а) Отрезки AK и AN, BK и BM, CN и CM попарно равны, так как это отрезки касательных, проведенных к окружности из одной точки (см. рисунок). Тогда:
откуда что и требовалось доказать.
Согласно теореме косинусов получаем:
откуда x = BK =
Таким образом, AK : KB = 5 : 7.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Не доказано утверждения пункта а), но обоснованно получен верный ответ в пункте б) без использования утверждения пункта а) Имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ в результате арифметической ошибки (описки) Имеется верное доказательство утверждения пункта а), получен верный ответ в пункте б), но решение недостаточно обоснованно, либо обоснования содержат неточности. | 2 |
| Имеется верное доказательство утверждения пункта а) при неверном доказательстве утверждения пункта а) и обоснованном решении пункта б) без использования утверждения пункта а) получен неверный ответ в результате арифметической ошибки (описки) обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен или выполнен неверно 📹 Видео🔴 В угол C, равный 165°, вписана окружность с ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать  Всё про углы в окружности. Геометрия | МатематикаСкачать  Окружность вписанная в треугольник и описанная около треугольника.Скачать  2181 в угол C величиной 79° вписана окружность которая касается сторон углаСкачать  В угол C величиной 83° вписана окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать  Геометрия В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке D, причёмСкачать 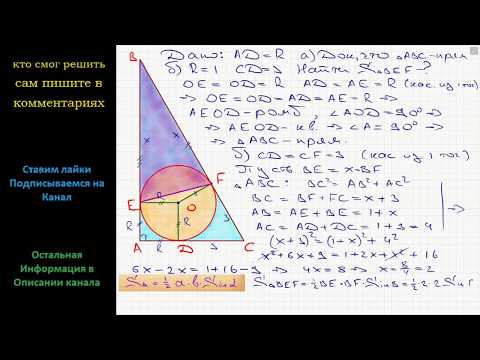 Видео урок / Геометрия: В угол величиной 70 градусов вписана окружность, которая касается его сторонСкачать 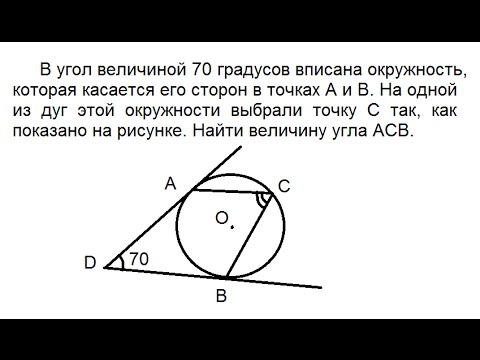 🔴 В угол C, равный 79°, вписана окружность ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать  2034 треугольник ABC вписан в окружность с центром в точке O точки O и C лежат в одной полуплоскостиСкачать  Геометрия В треугольнике ABC известны длины сторон AB = 18, AC = 36, точка O — центр окружностиСкачать  Геометрия Вписанная окружность касается сторон AB, AC, BC треугольника ABC в точках P, R, TСкачать  Задача про вписанную в треугольник окружность, из учебника Атанасяна номер 692Скачать  Вся геометрия треугольника в одной задаче. Планиметрия. ЕГЭ 2023 математика задача 16Скачать  №17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать  8.30.1. Планиметрия. Гордин Р.К.Скачать 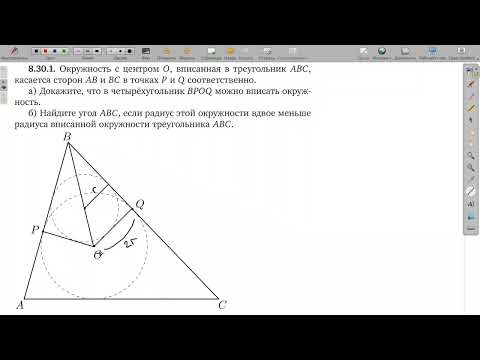 Треугольник ABC вписан в окружность с центром O Угол BAC равен 32°Скачать  #2_Самое сложное задание 16 ОГЭ 2021. Задачи по геометрии. Вписанные и центральные углы.Скачать  ОГЭ Задание 25 Демонстрационный вариант 2022, математикаСкачать 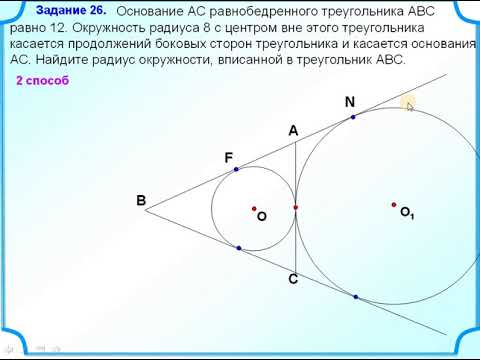 |


 BCA = 60 o .
BCA = 60 o .