В равнобедренной трапеции клмн расположены две окружности

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .

Видео:Ященко 2023, 12 вариантов. Вариант 3, задание 16.Скачать

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия –

Отношение площадей этих треугольников есть .

4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Видео:Задача про трапецию, описанную около окружностиСкачать

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Видео:Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать

Вписанная окружность

Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то

Видео:№388. Докажите, что в равнобедренной трапеции: а) углы при каждом основании равныСкачать

Площадь

или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:Трапеция. Задачи. Найти углы трапеции. Равнобедренной,прямоугольной,Скачать

Трапеция

Трапеция — это четырехугольник, у которого только две стороны параллельны,
а две другие стороны нет.

Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Элементы трапеции

Видео:КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

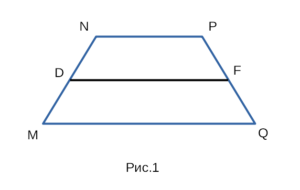
На рисунке 1 изображена трапеция MNPQ, с боковыми сторонами MN и PQ, с основаниями NP и MQ, а также со средней линией DF.

В трапеции две параллельные стороны называются основаниями. 0дна из параллельных сторон называется верхним основанием, а другая параллельная сторона называется нижним основанием. Но как определить, какая из параллельных сторон нижнее основание, а какая верхнее основание? Существует несколько способов это определить. Во-первых, как вы уже наверно догадались, нижнее основание расположено внизу трапеции, а верхнее основание расположено вверху трапеции. Во-вторых, верхнее основание меньше чем нижнее основание, и наоборот нижнее основание больше верхнего основания. C помощью этих двух способов вы можете
легко определить какое основание нижнее а какое верхнее. NP || MQ, NP — верхнее основание, MQ — нижнее основание.

Кроме оснований в трапеции, есть еще две не параллельные стороны. В трапеции эти две не параллельные стороны называются боковыми сторонами. Боковые стороны расположены сбоку от верхнего и нижнего оснований. MN и PQ — боковые стороны.

Отрезок, соединяющий середины боковых сторон называется средней линией трапеции. С средней линией трапеции связано несколько важных формул. Например, достаточно знать длину средней трапеции и одну из сторон основания, чтобы найти другое основание. Средняя линия делит две боковые стороны трапеции на две равных части. DF — средняя линия трапеции, MD = DN, QF = FP.

Центром симметрии трапеции называется середина средней линии трапеции. Центр симметрии
является центром вписанной, и центром описанной окружностей.

Видео:Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать

Виды трапеции

Также существует несколько видов трапеции. Это равнобедренная и прямоугольная трапеции.

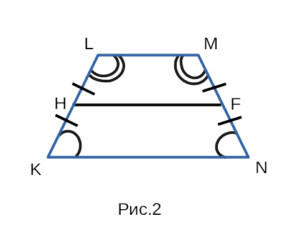
На рисунке 2 изображена равнобедренная трапеция KLMN, с боковыми сторонами KL и MN, с основаниями LM и KN, а также со средней линией HF.

В равнобедренной трапеции боковые стороны равны, углы при основаниях равны. KL = MN, ∠LKN = ∠MNK, ∠KLM = ∠NML.
Чтобы найти среднюю линию в равнобедренной трапеции достаточно знать только одну из боковых сторон.

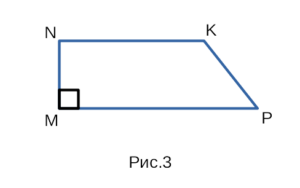
На рисунке 3 изображена прямоугольная трапеция MNKP, с боковыми сторонами MN и KP, с основаниями NK и MP, а также с прямым углом ∠NMP .

В прямоугольной трапеции у одной из боковых сторон есть прямой угол, или же по другом сказать — только одна боковая сторона перпендикулярна одному из оснований.
∠NMP — прямой угол.

Видео:СЕРЬЁЗНО готовимся к ОГЭ 2024! / Полный прогон задания 17 на ОГЭ по математикеСкачать

Задача 16760 Дана равнобедренная трапеция KLMN с.

Условие

Дана равнобедренная трапеция KLMN с основаниями KN и LM. Окружность с центром О, построенная на боковой стороне KL как на диаметре, касается боковой стороны MN и второй раз пересекает большее основание KN в точке Н, точка Q — середина MN.

а) Докажите, что четырёхугольник NQOH — параллелограмм.

б) Найдите KN, если угол LKN = 75° и LM = 4.

Решение

OQ-средняя линия трапеции KLMN
OQ||LM
OQ||KN ⇒ OQ||HN
OK=OL=OH=OB=r
Δ KOH- равнобедренный (ОК=ОН=r)
∠ OKH=∠OHK=75 градусов;

∠OHK=∠QNK=75 градусов, это односторонние углы, значит
OH||QN
NQOH- параллелограмм, так как противоположные стороны попарно параллельны:
OQ||HN
и
OH||QN

б)
Дано:
∠ LKN=∠MNK=75 градусов;
LM=4

Пусть боковые стороны трапеции LK и MN пересекаются в точке А.
∠ АLМ=∠ LKN=75 градусов;
∠АML=∠MNK=75 градусов;
Значит, ∠ АLМ=∠АML=75 градусов;
Δ ALM — равнобедренный
∠ LAM=180 градусов — ∠ АLМ-∠АML=180 градусов -75 градусов-75 градусов=30 градусов;

ΔАОВ- прямоугольный (OB⊥MN) с острым углом ∠ LAM=30 градусов, катет против угла в 30 градусов равен половине гипотенузы
ОА=2*ОВ=2*r

Тогда AL=AO-LO=2r-r=r
AL=AM=r
LM- средняя линия треугольника AOQ
OQ=2LM=2*4=8

ΔАLM=ΔKOH
AL=AM=OK=OH=r
LM=KH=4

🌟 Видео

Нафиг теорему синусов 3 задание проф. ЕГЭ по математике (часть II)Скачать

ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

№599. Найдите площадь равнобедренной трапеции с основаниями 2 см и 6 см, если уголСкачать

Окружность, вписанная в трапециюСкачать

В равнобедренной трапеции основания равны 2 и 8 ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

Трапеция, решение задач. Вебинар | МатематикаСкачать

Задание 25_Признак равнобедренной трапецииСкачать

8 класс, 6 урок, ТрапецияСкачать

Окружность и трапеция | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис Трушин +Скачать

В равнобедренной трапеции известна высота ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать