В равнобедренном тупоугольном треугольнике

Задание.

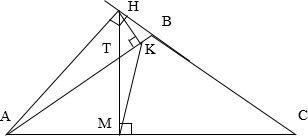
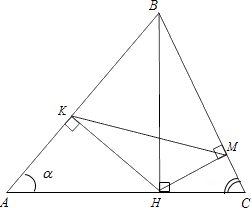
В равнобедренном треугольнике ABC, где угол B – тупой, на продолжение стороны BC опущена высота AH. ИЗ точки H на стороны AB и AC опущены перпендикуляры HK и HM соответственно.

а) Докажите, что AM = MK.

б) Найдите MK, если AB = 13, AC = 24.

Решение:

а) Докажите, что AM = MK.

Так как, угол AKH = 90 0 , угол AMH = 90 0 , тогда отрезок AH виден из точек K и M под углом 90 0 . Поэтому точки A, M, K и H лежат на окружности, диаметром которой является отрезок AH (см. рис.1).

Угол AKM — вписанный в окружность угол, который опирается на дугу AM. Угол AHM — вписанный в окружность угол, который опирается на дугу AM. Следовательно, угол AKM равен углу AHM. Т.е.

Треугольник ΔAHC – прямоугольный, тогда

Треугольник ΔAHM – прямоугольный, тогда

Из (1) и (2) равенства имеем, что

Так как треугольник ΔABC – равнобедренный (AB = BC), то

Тогда в треугольнике ΔAKM:

Получаем, что треугольник ΔAKM – равнобедренный и AM = MK.

б) Найдите MK, если AB = 13, AC = 24.

Рассмотрим треугольник ΔAMH – прямоугольный, угол AHM = α, MK = AM

Рассмотрим треугольник ΔABP – прямоугольный:

BP 2 = AB 2 – AP 2

BP 2 = 13 2 – 12 2 = 25

Найдем площадь треугольника ΔABC:

С другой стороны, площадь треугольника ΔABC можно найти

Тогда, AH = 2· S_ABC/BC

AH = (2·60)/13 = 120/13

Подставим полученные значения в равенство (1), получаем:

Видео:7 класс, 32 урок, Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Равнобедренный тупоугольный треугольник

Средняя оценка: 4.8

Всего получено оценок: 200.

Средняя оценка: 4.8

Всего получено оценок: 200.

Равнобедренный треугольник наиболее часто встречается в задачах по геометрии. Так сложилось, что равнобедренный треугольник не столь прост в решении, как правильный, но при этом обладает рядом интересных свойств, которые могут затруднить решение задачи.

Видео:Виды треугольниковСкачать

Равнобедренный треугольник

Равнобедренным треугольником называется треугольник, две стороны которого равны между собой. Тогда третья сторона называется основанием, а равные стороны считаются боковыми.

Рис. 1. Равнобедренный треугольник.

Любой равнобедренный треугольник имеет ряд свойств:

• Углы при основании равнобедренного треугольника равны.
• Медиана, проведенная к основанию равнобедренного треугольника является биссектрисой и высотой.

Именно эти два свойства определяют специфические особенности равнобедренных треугольников. Как и произвольные треугольник, равнобедренные треугольники бывают 3 видов:

• Остроугольные
• Прямоугольные
• Тупоугольные.

Углы при основании равнобедренного треугольника равны, а сумма углов треугольника всегда равна 180 градусам. Поэтому в равнобедренном и тупоугольном треугольнике наибольший угол всегда лежит напротив основания. Если такой угол лежал бы при основании, то сумма углов превысила бы 180 градусов, а это невозможно.

Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Тупоугольный треугольник

Тупой угол это угол больше 90 градусов. Очень часто тупоугольный треугольник стараются изобразить так, чтобы тупой угол находился у основания треугольника. Такой подход облегчает восприятие фигуры.

Рис. 2. Тупоугольный треугольник.

В любой треугольник тупой угол добавляет несколько особенностей:

• Две высоты тупоугольного треугольника будут проходить вне треугольника. Они падают на продолжение одной из сторон.
• Ортоцентр, т.е. точка пересечения высот треугольника будет находится за пределами треугольника.
• Два других угла треугольника всегда будут острыми.

Видео:Равнобедренный тупоугольный треугольникСкачать

Равнобедренный тупоугольный треугольник

Равнобедренный треугольник – это треугольник, который с одной стороны содержит в себе тупой угол, а с другой стороны имеет две равные между собой стороны.

Такой равнобедренный треугольник сложно воспринимать визуально. Дело в том, что с одной стороны тупоугольные треугольники ученики часто изображают так, чтобы тупой угол был при основании.

Но если тупой угол начертить в основании, то реальное основание тупоугольного равнобедренного треугольника будет визуально совпадать с боковой стороной. Такой подход очень часто приводит к ошибкам. Поэтому равнобедренный тупоугольный треугольник лучше рисовать с тупым углом напротив основания, а сам угол подписывать прямо на чертеже.

Рис. 3. Равнобедренный тупоугольный треугольник.

С другой стороны, этот подход не всегда помогает воспринимать фигуру именно как тупоугольный треугольник. Поэтому и нужно подписывать углы, а при решении доказывать или проверять условие на наличие доказательств существования тупого угла в треугольнике.

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Что мы узнали?

Мы узнали, что такое тупоугольный равнобедренный треугольник и какими особенностями он обладает. Поговорили о том, как лучше начертить тупоугольный треугольник и выделили проблемы, которые могут возникнуть с этим вопросом при решении задач.

Видео:Тупоугольный треугольник для острого умаСкачать

16. Планиметрия

Формат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие «буква» — «цифра» должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.

Примеры ответов: 7 или здесьисейчас или 3514

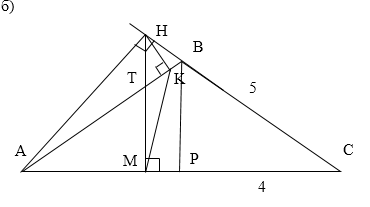
В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно.

а) Докажите, что отрезки AM и MK равны.

б) Найдите MK, если AB=5, AC=8.

Пусть $angle BAC=angle BCA=alpha .$ Тогда $angle ABC=180^-2alpha .$

$angle HBA=180^-180^+2alpha =2alpha $ как смежный с $angle ABC.$

Так как треугольник $AHB$ — прямоугольный, то $angle HAB=90^-2alpha .$

$angle HAC=angle HAB+angle BAC=90^-alpha .$

Так как треугольник $AHM$ — прямоугольный, то $angle AHM=90^-90^+alpha =alpha .$

Аналогично из прямоугольго треугольника $HKB$ получаем, что $angle BHK=90^-2alpha .$

Рассмотрим $angle AHB=90^=angle AHM+angle THK+angle BHK=alpha +angle THK+90^-2alpha Rightarrow angle THK=alpha .$

В треугольниках $ATM$ и $HTK$ $angle TAM=angle THK$ по доказанному, $angle AMT=angle HKT=90^$ по условию. Значит, данные треугольники подобны по призкаку подобия по 2 углам. Следовательно,

$displaystyle frac=displaystyle fracRightarrow displaystyle frac=displaystyle frac.$

В треугольнике $ATH$ и $MTK$ $angle ATH=angle MTK$ как вертикальные, $displaystyle frac=displaystyle frac$ по доказанномую Значит, данные треугольники подобны по 2 пропорциональнымсторонам и углу между ними. Тогда, $angle AHT=angle TKM=alpha .$

Получили, что в треугольнике $AKM$ углы при стороне $AK$ равны, значит, треугольник — равнобедренный и $AM=KM.$

Проведем прямую $BP//HM.$ В равнобедренном треугольнике $ABC$ отрезок $BP$ будет являться высотой и медианой, поэтому $PC=4.$ По теорем е Пифагора $BP^=sqrt<BC^-PC^>=3.$

Прямая $BP$ отсекает от треугольника $HCM$ подобные ему треугольник $BCP,$ поэтому $displaystyle frac=displaystyle frac,$

$displaystyle frac=displaystyle fracRightarrow HC=displaystyle fracCM.$

Обозначим $CM=x,$ тогда $HC=displaystyle fracx,$ $BH=displaystyle fracx-5,$ $AM=8-x.$

Из треугольника $ABH$ по теореме Пифагора $AH^=AB^-BH^=25-(displaystyle fracx-5)^=displaystyle fracx-displaystyle fracx^.$

Аналогично из треугольника $AHC$ $AC^=AH^+HC^$

$64=displaystyle fracx-displaystyle fracx^+displaystyle fracx^$

Дана трапеция с диагоналями равными 6 и 8. Сумма оснований равна 10.

а) Докажите, что диагонали перпендикулярны.

б) Найдите высоту трапеции.

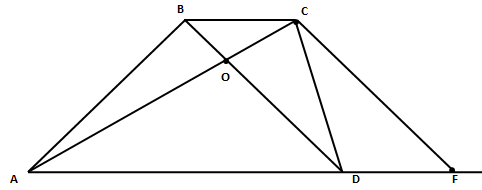
а) Проведем прямую CF//BD, тогда BCFD – параллелограмм и BC = DF, CF = BD.

В треугольнике ACF AC = 8, CF = 6, AF = AD + DF = 10.

Если диагонали перпендикулярны, то треугольник ACF – прямоугольный и выполняется теорема Пифагора:

Значит, угол между диагоналями равен 90⁰.

б) $S_=displaystyle fraccdot h=5h,$ , где h – длинна высоты.

С другой стороны $S_=displaystyle fraccdot BDcdot ACcdot sin 90^=24$

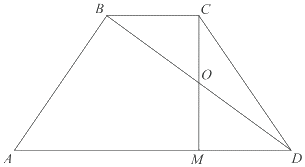
Дана равнобедренная трапеция, в которой AD = 3BC, CM — высота трапеции.

а) Доказать, что M делит AD в отношении 2:1.

б) Найдите расстояние от точки C до середины BD, если AD = 18, $AC=4sqrt.$.

а) Поскольку ABCD — равнобедренная трапеция, то

$MD=displaystyle frac=displaystyle frac=BC$

Тогда $AM=2BC$. Следовательно, $displaystyle frac=displaystyle frac$

Треугольник AMC прямоугольный. В нем $AM=displaystyle fracAD=12$ по доказанному в пункте а) и $AC=4sqrt$ по условию.

По теореме Пифагора $CM^+AM^=AC^$ , откуда $CM=8$ .

Треугольники BCO и MOD равны по катету и острому углу (BC=MD по доказанному в пункте а) , углы CBO и ADO равны как накрест лежащие). Тогда BO = OD и СO = OM как соответственные элементы равных треугольников. Значит, СO — искомое расстояние.

В остроугольном треугольнике ABC провели высоту BH из точки H на стороны AB и BC опустили перпендикуляры HK и HM соответственно.

а) Докажите, что треугольник MBK подобен треугольнику ABC.

б) Найдите отношение площади треугольника MBK к площади четырёхугольника AKMC, если BH = 2, а радиус окружности, описанной около треугольника ABC равен 4.

а) Обозначим $angle BAC=alpha .$. Треугольники AKH, CMH, ABH и BKH – прямоугольные. Тогда $angle KHA=angle ABH=90^-alpha .$. Аналогично $angle KHB=90^-(90^-alpha )=alpha .$. В четырехугольнике BKHM $angle BKH+angle BMH=90^+90^=180^,$, значит, вокруг этого четырехугольника можно описать окружность. Углы $angle KHB=angle KMB=alpha $ как опирающиеся на одну и ту же хорду.

В треугольниках ABC и MKB $angle KMB=angle BAC,angle ABC$ — совпадающий. Значит, они подобны по признаку подобия по 2 углам.

б) Обозначим k – коэффициент подобия треугольников ABC и MKB (k

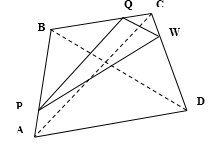
Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB=CQ:QB=CW:WD=1:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ=16, QW=12, угол PWQ — острый.

а) Докажите, что треугольник PQW — прямоугольный.

б) Найдите площадь четырёхугольника ABCD.

а) По теореме синусов из треугольника $PQW:$

$sin angle PWQ=displaystyle frac,sin angle QPW=displaystyle frac.$

Заметим, что $sin ^angle PWQ+sin ^angle QPW=displaystyle frac+displaystyle frac=1.$

$sin ^angle QPW=cos ^angle PWQ,$

$sin angle QPW=cos angle PWQ,$

так как угол $QWP$ — острый. Тогда $angle QPW+angle PWQ=90^$ и треугольник $PQW$ — прямоугольный.

б) Треугольник $PBQ$ и $ABC$ подобные по двум стронам и углу между ими ($angle B$ — общий, $displaystyle frac=displaystyle frac=displaystyle frac).$ Значит, $ACparallel PQ$ и $AC=displaystyle fracPQ=20.$

Аналогично, из подобия треугольников $QCW$ и $BCQ$ получаем, что $BDparallel QW$ и $BD=5QN=60$

Угол между прямыми $BD$ и $AC$ равен углу между прямыми $PQ$ и $QW,$ поэтому

$S_=displaystyle fracBDcdot ACcdot sin 90^=displaystyle frac60cdot 20=600.$

🎦 Видео

В тупоугольном треугольнике все углы тупые. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Равнобедренный треугольник. 7 класс.Скачать

Геометрия Основание равнобедренного тупоугольного треугольника равно 24 см, а радиус окружностиСкачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Задача 6 №27350 ЕГЭ по математике. Урок 42Скачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

32. Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Вся теория о треугольниках | Остроугольный, Прямоугольный и тупоугольный треугольник |Мир МатематикаСкачать

№254. Найдите углы равнобедренного прямоугольного треугольника.Скачать

КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать

Математика | Метрические соотношения в прямоугольном треугольникеСкачать