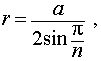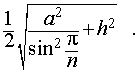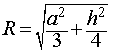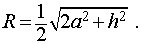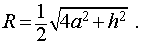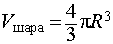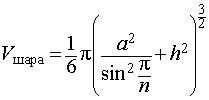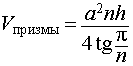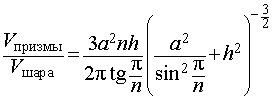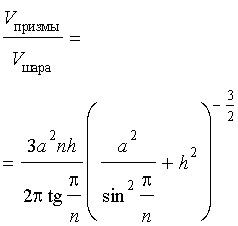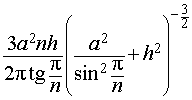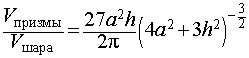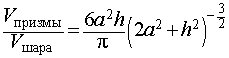В правильную треугольную призму вписана сфера радиус окружности 13

У правильной треугольной призмы радиус описанного шара равен 13см, а сторона основания — 53см. Найдите площадь боковой поверхности призмы.

• Танечка Нищик
• Геометрия 2018-12-31 19:18:17 10 1

Около призмы можно обрисовать сферу тогда и только тогда, когда призма — ровная, а около её оснований можно обрисовать окружность.

Шар описан около призмы, значит, призма ровная, все её верхушки лежат на поверхности шара.

Плоскость каждого из оснований призмы пересекает сферу по окружности, описанной около основания.

Так как основания — правильные треугольники, радиус таковой окружности равен 2/3 вышины АВС=а/3=5 см.

Отрезок КМ, соединяющий центры окружностей, обрисованных около оснований призмы, параллелен боковому ребру и равен ему. Центр сферы лежит на середине О этого отрезка.

Соединим О с А и К. Т.к. КМ перпендикулярен основаниям призмы, треугольник АКО прямоугольный.

По т.Пифагора КО=(AO-AK)=(13*-5)=12 см

АА1=КМ=2КО=24 см

Площадь боковой поверхности прямой призмы одинакова творению её вышины на периметр основания.

S=24353=3603 см

Видео:Радиус описанной окружностиСкачать

Многогранники, описанные около сферы

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Многогранники, описанные около сферы
Многогранник называется описанным около сферы, если плоскости всех его граней касаются сферы. Сама сфера называется вписанной в многогранник.
Теорема. В призму можно вписать сферу тогда и только тогда, когда в ее основание можно вписать окружность, и высота призмы равна диаметру этой окружности.
Теорема. В любую треугольную пирамиду можно вписать сферу, и притом только одну.

Сфера, вписанная в куб

Сфера, вписанная в куб
На рисунке изображена сфер, вписанная в куб.

Упражнение 1
Сотрите квадрат и нарисуйте два параллелограмма, изображающих верхнюю и нижнюю грани куба. Соедините их вершины отрезками. Получите изображение сферы, вписанной в куб.
Изобразите сферу, вписанную в куб, как на предыдущем слайде. Для этого изобразите эллипс вписанный в параллелограмм, полученные сжатием окружности и квадрата в 4 раза. Отметьте полюса сферы и точки касания эллипса и параллелограмма.

Упражнение 2
Найдите радиус сферы, вписанной в единичный куб.
Ответ:

Упражнение 3
В куб вписана сфера радиуса 1. Найдите ребро куба.
Ответ: 2.

Упражнение 4
Можно ли вписать сферу в прямоугольный параллелепипед, отличный от куба?
Ответ: Нет.

Упражнение 5
Можно ли вписать сферу в наклонный параллелепипед, все грани которого ромбы?
Ответ: Нет.

Сфера, вписанная в треугольную призму

Упражнение 1
Можно ли вписать сферу в наклонную треугольную призму, в основании которой правильный треугольник?
Ответ: Нет.

Упражнение 2
Найдите высоту правильной треугольной призмы и радиус, вписанной в нее сферы, если ребро основания призмы равно 1.
Ответ:

Упражнение 3
В правильную треугольную призму вписана сфера радиуса 1. Найдите сторону основания и высоту призмы.
Ответ:

Упражнение 4
В призму, в основании которой прямоугольный треугольник с катетами, равными 1, вписана сфера. Найдите радиус сферы и высоту призмы.
Площадь треугольника ABC равна , периметр
Воспользуемся формулой r = S/p. Получим

Упражнение 5
В призму, в основании которой равнобедренный треугольник со сторонами 2, 3, 3, вписана сфера. Найдите радиус сферы и высоту призмы.
Площадь треугольника ABC равна Периметр равен 8.
Воспользуемся формулой r = S/p. Получим

Сфера, вписанная в четырехугольную призму

Упражнение 1
Сфера вписана в прямую четырехугольную призму, в основании которой ромб со стороной 1 и острым углом 60о. Найдите радиус сферы и высоту призмы.
Решение. Радиус сферы равен половине высоты DG основания, т.е.

Высота призмы равна диаметру сферы, т.е.

Упражнение 2
Единичная сфера вписана в прямую четырехугольную призму, в основании которой ромб с острым углом 60о. Найдите сторону основания a и высоту призмы h.
Ответ:

Упражнение 3
Сфера вписана в прямую четырехугольную призму, в основании которой трапеция. Высота трапеции равна 2. Найдите высоту призмы h и радиус r вписанной сферы.
Ответ:

Упражнение 4
Сфера вписана в прямую четырехугольную призму, в основании которой четырехугольник, периметра 4 и площади 2. Найдите радиус r вписанной сферы.
Решение. Заметим, что радиус сферы равен радиусу окружности, вписанной в основание призмы.
Воспользуемся тем, что радиус окружности, вписанной в многоугольник, равен площади этого многоугольника делёной на его полупериметр. Получим,

Сфера, вписанная в правильную шестиугольную призму

Упражнение 1
Найдите высоту правильной шестиугольной призмы и радиус, вписанной в нее сферы, если сторона основания призмы равна 1.
Ответ:

Упражнение 2
В правильную шестиугольную призму вписана сфера радиуса 1. Найдите сторону основания и высоту призмы.
Ответ:

Сфера, вписанная в правильный тетраэдр

Упражнение 1
Найдите радиус сферы, вписанной в единичный тетраэдр.
Ответ:
Решение. В тетраэдре SABC имеем:
SD = DE = SE =
Из подобия треугольников SOF и SDE получаем уравнение

решая которое, находим

Упражнение 2
В правильный тетраэдр вписана единичная сфера. Найдите ребро этого тетраэдра.
Ответ:

Упражнение 3
Найдите радиус сферы, вписанной в правильную треугольную пирамиду, сторона основания которой равна 2, и двугранные углы при основании равны 60о.
Решение. Воспользуемся тем, что центр вписанной сферы является точкой пересечения биссектральных плоскостей двугранных углов при основании пирамиды. Для радиуса сферы OE имеет место равенство

Упражнение 4
Найдите радиус сферы, вписанной в правильную треугольную пирамиду, боковые ребра которой равны 1, и плоские углы при вершине равны 90о.
Ответ:
Решение. В тетраэдре SABC имеем:
SD = DE = SE =
Из подобия треугольников SOF и SDE получаем уравнение

решая которое, находим

Сфера, вписанная в четырехугольную пирамиду

Упражнение 1
Найдите радиус сферы, вписанной в правильную четырехугольную пирамиду, все ребра которой равны 1.
Воспользуемся тем, что для радиуса r окружности, вписанной в треугольник, имеет место формула: r = S/p, где S – площадь, p – полупериметр треугольника.
В нашем случае S = p =
Решение. Радиус сферы равен радиусу окружности, вписанной в треугольник SEF,
в котором SE = SF = EF=1, SG =
Следовательно,

Упражнение 2
Найдите радиус сферы, вписанной в правильную четырехугольную пирамиду, сторона основания которой равна 1, а боковое ребро — 2.
Воспользуемся тем, что для радиуса r окружности, вписанной в треугольник, имеет место формула: r = S/p, где S – площадь, p – полупериметр треугольника.
В нашем случае S = p =
Решение. Радиус сферы равен радиусу окружности, вписанной в треугольник SEF,
в котором SE = SF = EF=1, SG =
Следовательно,

Упражнение 3
Найдите радиус сферы, вписанной в правильную четырехугольную пирамиду, сторона основания которой равна 2, и двугранные углы при основании равны 60о.
Решение. Воспользуемся тем, что центр вписанной сферы является точкой пересечения биссектральных плоскостей двугранных углов при основании пирамиды. Для радиуса сферы OG имеет место равенство

Упражнение 4
Единичная сфера вписана в правильную четырехугольную пирамиду, сторона основания которой равна 4. Найдите высоту пирамиды.
Воспользуемся тем, что для радиуса r окружности, вписанной в треугольник, имеет место формула: r = S/p, где S – площадь, p – полупериметр треугольника.
В нашем случае S = 2h, p =
Решение. Обозначим высоту SG пирамиды h. Радиус сферы равен радиусу окружности, вписанной в треугольник SEF, в котором
SE = SF = EF=4.
Следовательно, имеем равенство
из которого находим

Сфера, вписанная в правильную шестиугольную пирамиду

Упражнение 1
Найдите радиус сферы, вписанной в правильную шестиугольную пирамиду, у которой ребра основания равны 1, а боковые ребра — 2.
Воспользуемся тем, что для радиуса r окружности, вписанной в треугольник, имеет место формула: r = S/p, где S – площадь, p – полупериметр треугольника.
В нашем случае S = p =
Следовательно,
Решение. Радиус сферы равен радиусу окружности, вписанной в треугольник SPQ,
в котором SP = SQ = PQ= SH =

Упражнение 2
Найдите радиус сферы, вписанной в правильную шестиугольную пирамиду, у которой ребра основания равны 1, и двугранные углы при основании равны 60о.
Решение. Воспользуемся тем, что центр вписанной сферы является точкой пересечения биссектральных плоскостей двугранных углов при основании пирамиды. Для радиуса сферы OH имеет место равенство

Сфера, вписанная в октаэдр

Упражнение
Найдите радиус сферы, вписанной в единичный октаэдр.
Ответ:
Решение. Радиус сферы равен радиусу окружности, вписанной в ромб SES’F, в котором SE = SF =
EF=1, SO = Тогда высота ромба, опущенная из вершины E , будет
равна
Искомый радиус равен половине
высоты, и равен

Сфера, вписанная в икосаэдр

Упражнение
Найдите радиус сферы, вписанной в единичный икосаэдр.
Решение. Воспользуемся тем, что радиус OA описанной сферы
равен а радиус AQ
окружности, описанной около равностороннего треугольника со стороной 1, равен
По теореме Пифагора, примененной к прямоугольному треугольнику OAQ, получим

Сфера, вписанная в додекаэдр

Упражнение
Найдите радиус сферы, вписанной в единичный додекаэдр.
Решение. Воспользуемся тем, что радиус OF описанной сферы
равен а радиус FQ
окружности, описанной около равностороннего пятиугольника со стороной 1, равен
По теореме Пифагора, примененной к прямоугольному треугольнику OFQ, получим

Упражнение 1
Можно вписать сферу в усеченный тетраэдр?
Решение. Заметим, что центр O сферы, вписанной в усеченный тетраэдр должен совпадать с центром сферы, вписанной в тетраэдр, который совпадает с центром сферы, полувписанной в усеченный тетраэдр. Расстояния d1, d2 от точки O до шестиугольной и треугольной граней вычисляются по теореме Пифагора:
где R – радиус полувписанной сферы, r1, r2 – радиусы окружностей, вписанных в шестиугольник и треугольник, соответственно.
Поскольку r1 > r2, то d1

Курс повышения квалификации

Охрана труда

• Сейчас обучается 99 человек из 45 регионов

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

• Сейчас обучается 350 человек из 64 регионов

Курс профессиональной переподготовки

Охрана труда

• Сейчас обучается 219 человек из 53 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Вычисление радиуса сферы, вписанной в правильную треугольную пирамидуСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 530 877 материалов в базе

Другие материалы

• 27.12.2020
• 4376
• 0

• 27.12.2020
• 4533
• 11

• 27.12.2020
• 5109
• 8

• 27.12.2020
• 4548
• 3

• 27.12.2020
• 3817
• 1

• 27.12.2020
• 3684
• 0

• 27.12.2020
• 3696
• 1

• 27.12.2020
• 3007
• 1

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 19.10.2020 1023
• PPTX 1.5 мбайт
• 69 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Светличная Светлана Михайловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 1 год и 1 месяц
• Подписчики: 0
• Всего просмотров: 29489
• Всего материалов: 230

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Быстро находим радиус описанной сферыСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Студенты на Северном Кавказе бесплатно подготовят к ЕГЭ сельских школьников

Время чтения: 1 минута

В ЕГЭ обновили задания по математике

Время чтения: 2 минуты

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Петербургских школьников с 7 по 11 классы перевели на дистанционное обучение

Время чтения: 1 минута

В Оренбурге продлили дистанционное обучение для школьников

Время чтения: 1 минута

В Курганской области школьников переведут на дистанционное обучение с 4 февраля

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:ЕГЭ Задание 14 Пирамида вписана в сферуСкачать

Призма, вписанная в сферу

Призма, вписанная в сферу. Свойства призмы, вписанной в сферу

Радиус сферы, описанной около правильной n — угольной призмы

Отношение объема правильной n — угольной призмы к объему шара, ограниченного описанной около этой призмы сферой

Видео:Щелчок по математике I №1,2 Решаем прототипы ФИПИ всех видовСкачать

Призма, вписанная в сферу. Свойства призмы, вписанной в сферу

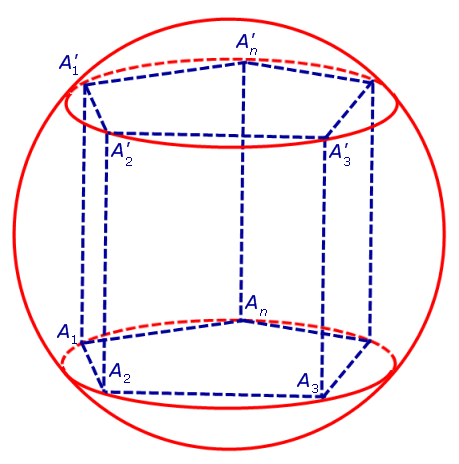
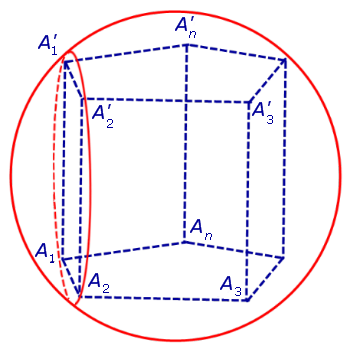
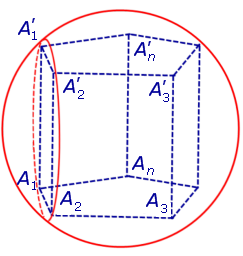
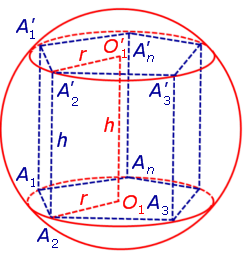
Определение 1. Призмой, вписанной в сферу, называют такую призму, все вершины которой лежат на сфере (рис. 1).

Определение 2. Если призма вписана в сферу, то сферу называют описанной около призмы.

Теорема. Около призмы можно описать сферу тогда и только тогда, когда выполнены следующие два условия:

1. Призма является прямой призмой;
2. Около оснований призмы можно описать окружности.

Доказательство. Докажем сначала, что если n – угольная призма A₁A₂ . A_nA’₁A’₂ . A’_n вписана в сферу, то оба условия теоремы выполнены.

Для этого заметим, что плоскость каждого из оснований призмы пересекает сферу по окружности, на которой лежат вершины этого основания. Таким образом, многоугольники, являющиеся основаниями призмы, оказываются вписанными в окружности (рис. 1), то есть второе условие теоремы выполнено.

Каждая из боковых граней призмы также вписана в окружность (рис. 2).

Рассмотрим какое-нибудь боковое ребро призмы, например, A₂A’₂. Поскольку это ребро перпендикулярно к ребрам основания A₁A₂ и A₂A₃ , то в силу признака перпендикулярности прямой и плоскости заключаем, что боковое ребро A₂A’₂ перпендикулярно к плоскости основания призмы, то есть призма является прямой призмой.

Таким образом, мы доказали, что, если призма вписана в сферу, то оба условия теоремы выполнены.

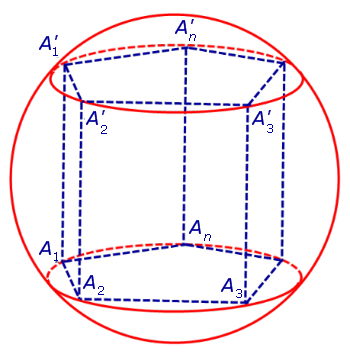
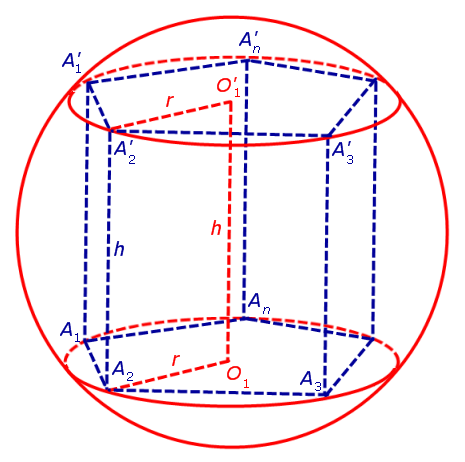
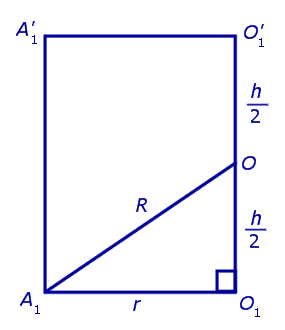
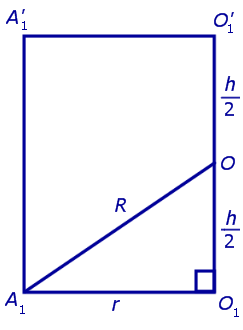
Для этого обозначим символом O₁ центр окружности радиуса r , описанной около нижнего основания призмы, а символом O’₁ обозначим центр окружности, описанной около верхнего основания призмы (рис. 3).

Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы описанных около них окружностей будут равны.

Согласно утверждению 1 из раздела «Призмы, вписанные в цилиндры» отрезок O₁O’₁, соединяющий центры окружностей, описанных около нижнего и верхнего оснований призмы, параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок O₁O’₁ перпендикулярен плоскости основания призмы и равен h.

Обозначим буквой O середину отрезка O₁O’₁ и докажем, что все вершины призмы будут находиться на одном и том же расстояниии от точки O (рис. 4).

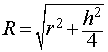(1)

от всех вершин призмы. Отсюда следует, что точка O является центром сферы радиуса R , описанной около призмы.

Следствие 1. Около любой прямой треугольной призмы можно вписать сферу.

Следствие 2. Около любого прямоугольного параллелепипеда (в частности, около куба прямоугольного параллелепипеда (в частности, около куба ) можно описать сферу.

Следствие 3. Около любой правильной призмы можно описать сферу.

Для доказательства следствия 3 достаточно заметить, что правильная n – угольная призма – это прямая призма, основания которой являются правильными n – угольниками, а около любого правильного n – угольника можно описать окружность.

Видео:Все Задания 3 ЕГЭ 2024 ПРОФИЛЬ из Банка ФИПИ (Математика Школа Пифагора)Скачать

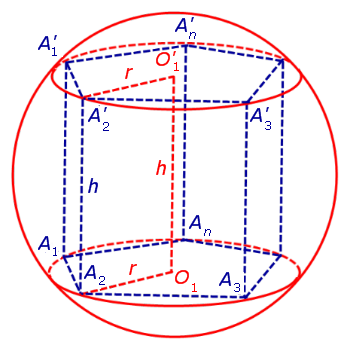
Радиус сферы, описанной около правильной n — угольной призмы

то из формулы (1) получаем выражение для радиуса описанной сферы

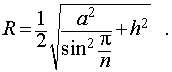(2)

Ответ.

Следствие 6. Радиус сферы, описанной около около правильной шестиугольной призмы с высотой h и ребром основания a равен

Видео:ЕГЭ по математике - Шар в пирамидеСкачать

Отношение объема правильной n — угольной призмы к объему шара, ограниченного описанной около призмы сферой

Задача 2. Около правильной n — угольной призмы с высотой h и ребром основания a описана сфера. Найти отношение объемов призмы и шара, ограниченного сферой, описанной около данной призмы.

Воспользовавшись формулой (2), выразим объем шара, ограниченного описанной около призмы сферой, через высоту и ребро основания призмы:

Ответ.

Следствие 7. Отношение объема правильной треугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Следствие 8. Отношение объема правильной четырехугольной призмы правильной четырехугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Следствие 9. Отношение объема правильной шестиугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

📽️ Видео

Вписанная и описанная окружность - от bezbotvyСкачать

ПЛОЩАДЬ КОЛЬЦА. Сделай выбор: на чьей ты стороне?Скачать

Треугольная пирамида. Найдите радиус вписанной сферыСкачать

Длина окружности. Площадь круга. 6 класс.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Решаем стереометрию 13 задание подряд | ЕГЭ математика 2023 | Часть 2Скачать

5.2. Многогранник, описанный вокруг сферы.Скачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

11 класс, 19 урок, Сфера и шарСкачать

1 2 4 сопряжение окружностейСкачать

SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

11 класс, 26 урок, Сфера, вписанная в коническую поверхностьСкачать

Разбор всех №1 и №3 из сборника Ященко 2024Скачать