В правильной треугольной призме ABCA1B1C1 сторона AB основания равна 12, а высота призмы равна 2. На рёбрах B1C1 и AB отмечены точки P и Q соответственно, причём PC1 = 3, а AQ = 4. Плоскость A1PQ пересекает ребро BC в точке M.
а) Докажите, что точка M является серединой ребра BC.
б) Найдите расстояние от точки B до плоскости A1PQ.
а) Пусть прямые A1Q и BB1 пересекаются в точке R (см. рисунок). Тогда точка M — точка пересечения прямых PR и BC.
Треугольники PB1R и MBR подобны, откуда
Значит, M — середина BC.
б) Расстояние от точки B до плоскости A1PQ равно высоте h пирамиды BRQM, опущенной из вершины B. Значит, с одной стороны, объём пирамиды BRQM
C другой стороны, 
Таким образом,
Найдем стороны треугольника QMR:
Площадь равнобедренного треугольника QMR равна
Следовательно, 
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Содержание Видео:Задача №14 ЕГЭ профиль геометрия. В правильной треугольной призме ABCA1B1C1Скачать 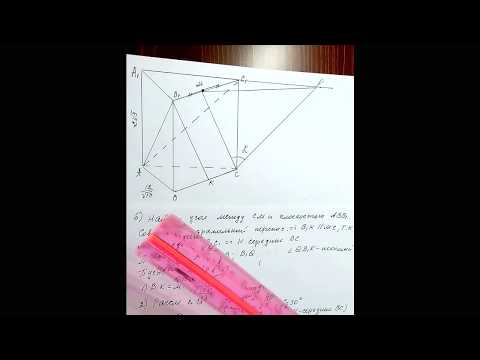 В правильной треугольной призме ABCA1B1C1324451. В правильной треугольной призме ABCA1B1C1 стороны оснований равны 2, боковые рёбра равны 5. Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер АВ, АС, A1B1 и A1C1. Проект «МатематикаЕГЭ» — Решение задач из открытого банка заданий ЕГЭ Видео:Угол между прямыми Треугольная призмаСкачать  Репетитор по математикеМеня зовут Виктор Андреевич, — я репетитор по математике . Последние десять лет я занимаюсь только преподаванием. Я не «натаскиваю» своих учеников. Моя цель — помочь ребенку понять предмет, научить его мыслить, а не применять шаблоны, передать свои знания, а не просто «добиться результата». Предусмотрен дистанционный формат занятий (через Skype или Zoom). На первом же уроке оцениваем уровень подготовки ребенка. Если ребенка устраивает моя подача материала, то принимаем решение о дальнейшем сотрудничестве — составляем расписание и индивидуальный план работы. После каждого занятия дается домашнее задание — оно всегда обязательно для выполнения. [в личном кабинете родители могут контролировать успеваемость ребенка]
Стоимость занятийНабор на 2020/2021 учебный год открыт. Предусмотрен дистанционный формат. Видеокурсы подготовки к ЕГЭ-2021Решения авторские, то есть мои (автор ютуб-канала mrMathlesson — Виктор Осипов). На видео подробно разобраны все задания. Теория представлена в виде лекционного курса, для понимания методик, которые используются при решении заданий. Видео:Стереометрия 7 | mathus.ru | угол между прямыми в правильной треугольной призмеСкачать  Группа ВконтактеВ группу выкладываются самые свежие решения и разборы задач. Подпишитесь, чтобы быть в курсе и получать помощь от других участников.
Видео:🔴 Сторона основания правильной треугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать  ПреимуществаПедагогический стажСейчас существует много сайтов, где вам подберут репетитора по цене/опыту/возрасту, в зависимости от желаний. Но большинство анкет там принадлежат либо студентам, либо школьным учителям. Для них репетиторство — дополнительный временный заработок, из этого формируется отношение к деятельности. У студентов нет опыта и желания совершенствоваться, у школьных учителей — нет времени и сил после основной деятельности. Я занимаюсь только репетиторством с 2010 года. Все свои силы и знания трачу на совершенствование только в этой области. Собственная методикаЗа время работы я накопил огромное количество материала для подготовки к итоговым экзаменам. Ребенку не будет даваться неадаптированная школьная программа. С каждым я разберу поэтапно специфичные примеры, темы, способы решений, необходимые для успешной сдачи ЕГЭ и ОГЭ. При этом это не будет «натаскиванием» на решение конкретных задач, но полноценная структурированная подготовка. Естественно, если таковые найдутся, устраню «пробелы» и в школьной программе. Гарантированный результатЗа время моей работы не было ни одного случая, где не прослеживалась бы четкая тенденция к улучшению знаний у ученика. Ни один откровенно не «завалил» экзамен. Каждый вырос в «понимании» математики в сравнении со своим первоначальным уровнем. Естественно, я не могу гарантировать, что двоечник за полгода подготовится на твердую «пять». Но могу с уверенностью сказать, что я подготовлю ребенка на его максимально возможный уровень за то время, что осталось до экзамена. Индивидуальная работаВсе дети разные, поэтому способ и форма объяснения корректируются в зависимости от уровня понимания ребенком предмета. Индивидуальная работа с каждым учеником — каждому даются отдельные задания, теоретический материал. 🌟 ВидеоВсе рёбра правильной треугольной призмы имеют длину 6Скачать  Геометрия В правильной треугольной призме через сторону нижнего основания и противоположную вершинуСкачать  Геометрия Дана правильная треугольная призма ABCA1B1C1, у которой сторона основания равна 2Скачать  Геометрия На боковых ребрах BB1 и CC1 правильной треугольной призмы ABCA1B1C1 отмечены точкиСкачать  В правильной треугольной призме сторона основания равнаСкачать  В сосуд, имеющий форму правильной треугольной призмыСкачать  Стереометрия 23 | mathus.ru | угол между плоскостями в правильной треугольной призмеСкачать  Стереометрия 36 |mathus.ru| расстояние между скрещивающимися прямыми в правильной треугольной призмеСкачать  ЕГЭ 2017. Стереометрия. Угол между скрещивающимися прмыми. Пример из" варианты Ященко".Скачать  №230. Основание прямой призмы — треугольник со сторонами 5 см и 3 см и углом, равным 120Скачать  СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать  №229. В правильной n-угольной призме сторона основания равна а и высота равна h. ВычислитеСкачать  №233. Основанием прямой призмы АВСA1B1C1 является прямоугольный треугольник ABCСкачать  №221. Сторона основания правильной треугольной призмы равна 8 см, боковое ребро равно 6 смСкачать  Все ребра правильной треугольной призмы имеют длину 6. Докажите, что прямые BM и MN перпендикулярныСкачать  Урок 3. Как найти угол между прямой и плоскостью || Задание №13. Стереометрия на ЕГЭСкачать  |
Правильная треугольная призма это прямая призма в основании которой лежит правильный треугольник. Так как сечение проходит через середины сторон, то оно пересекает основания проходя через среднюю линию треугольников лежащих в основаниях. То есть сечение у нас это прямоугольник со сторонами 2 и 2,5.
