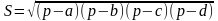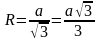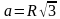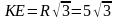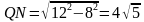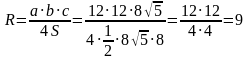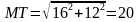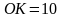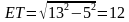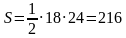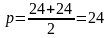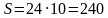В окружности треугольник ref

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Равносторонний треугольник в окружностиСкачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
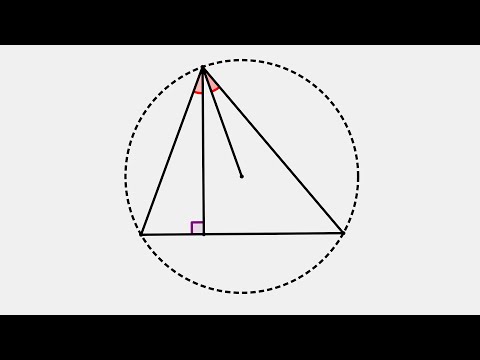
  формуле Герона.

Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Видео:Треугольник и окружность #shortsСкачать

Подготовка к контрольной работе

Урок №8. СКАЧИВАЙТЕ файл на устройства, чтобы все знаки и формулы были видны и распознаны. Во время чтения файла онлайн происходит потеря формул.

Просмотр содержимого документа
«Подготовка к контрольной работе»

Тема: Подготовка к контрольной работе

Задачи: обобщить и систематизировать теоретически знания и умения решать задачи по теме.

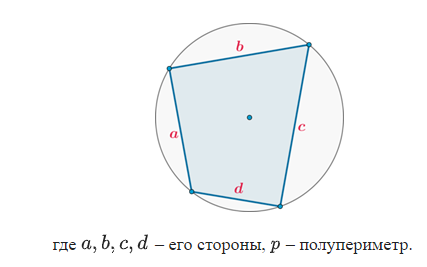
Если около четырехугольника можно описать окружность, то его площадь равна

Если в четырехугольник можно вписать окружность, то его площадь равна

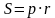
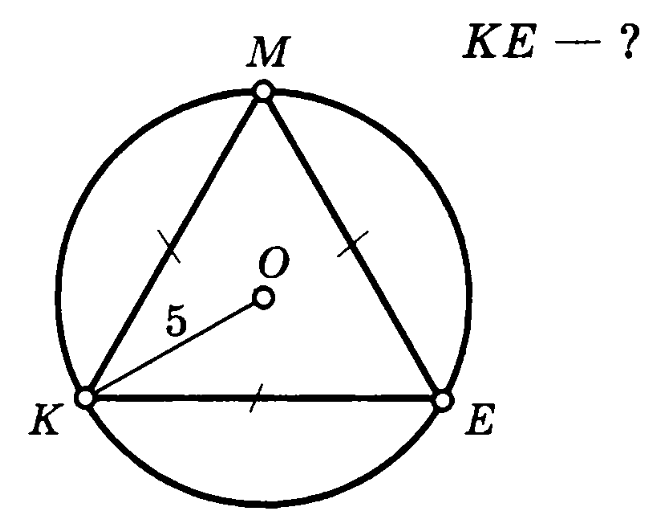
Задача 1. Равносторонний треугольник KME вписан в окружность радиуса 5. Найти сторону треугольника.

Решение (краткое). Воспользуемся формулой для радиуса описанной окружности около равностороннего треугольника:

Преобразуем её в формулу для нахождения стороны:

Тогда сторона треугольника:

Ответ: .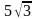

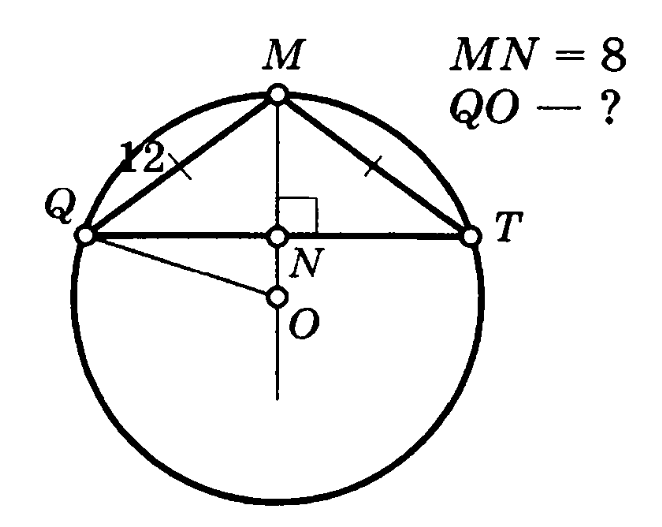
Задача 2. Равнобедренный треугольник QMT вписан в окружность. Высота треугольника MN=8, боковая сторона QM=MT=12. Найти радиус окружности.

Решение (краткое). Найдем QN из треугольника QMN:

Тогда сторона QT= .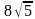

Применим формулу для нахождения радиуса описанной окружности:

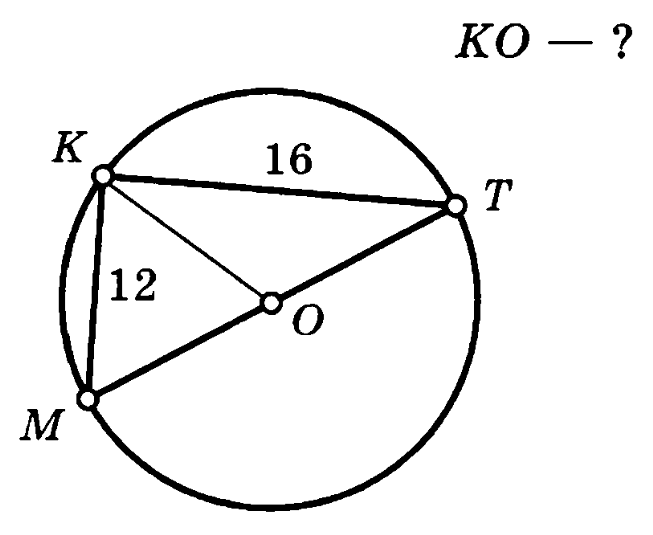
Задача 3. Треугольник MKT вписан в окружность, угол MKT опирается на диаметр. Стороны треугольника KM=12, KT=16. Найти радиус окружности.

Решение (краткое). Найдем длину стороны MT:

Т.к. MT – это диаметр окружности, то радиус вдвое меньше.

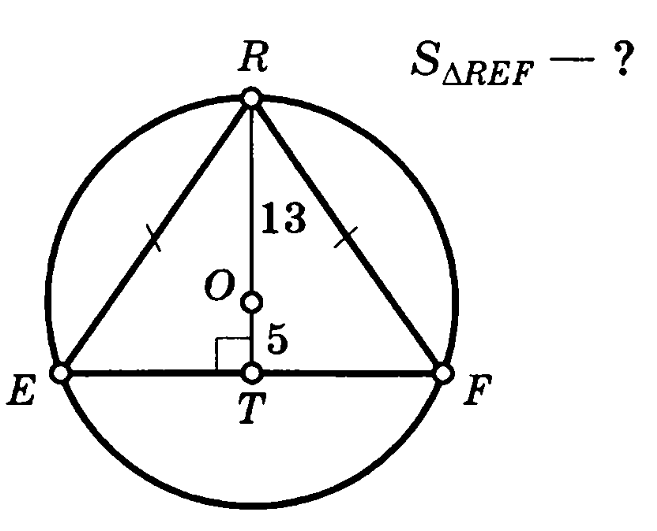
Задача 4. Равнобедренный треугольник REF вписан в окружность. Центр окружности делит высоту треугольника RS на отрезки RO=13 и OT=5. Найти площадь треугольника REF.

Решение (краткое). RO=OE=OF=13. Найдем ET:

Тогда сторона EF=2ET=24.

Найдем площадь треугольника:

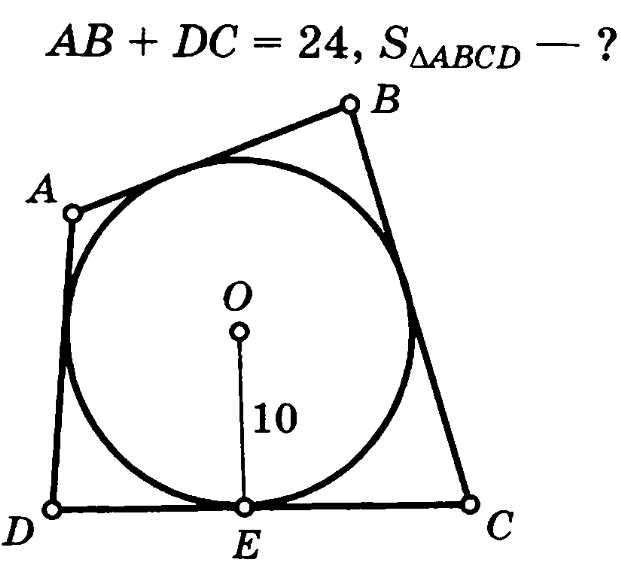
Задача 5. В четырехугольник ABCD вписана окружность радиуса 10. Сумма противоположных сторон четырехугольника равна 24. Найти площадь четырехугольника.

Решение (краткое). Найдем площадь четырехугольника по формуле .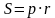

По свойству AB+DC=AD+BC=24, тогда полупериметр равен:

Тогда

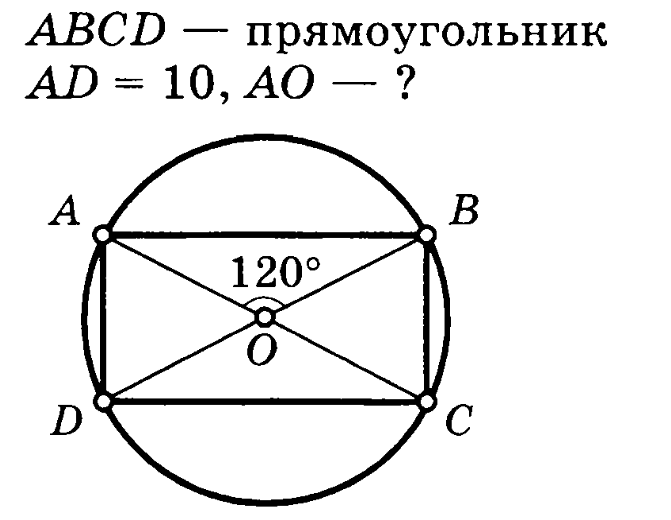
Задача 6. Прямоугольник ABCD вписан в окружность. Меньшая из его сторон равна 10, а тупой угол между диагоналями равен 120°. Найти радиус окружности.

Решение (краткое). Угол AOD=60°, AO=DO, следовательно, треугольник AOD равносторонний. AO=10.

ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ

Домашнее задание: подготовиться к контрольной работе, вспомнить теорию и решения задач.

Видео:Радиус описанной окружностиСкачать

Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов

Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.

Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.

Вокруг любого треугольника можно описать окружность, причем только одну.

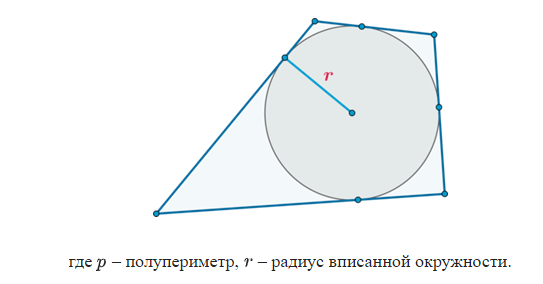
Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.

В любой треугольник можно вписать окружность, причем только одну.

Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник.

Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?

В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.

Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов.

Вот еще две формулы для площади.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.

— радиус окружности, вписанной в треугольник.

Есть и еще одна формула, применяемая в основном в задачах части :

где — стороны треугольника, — радиус описанной окружности.

Для любого треугольника верна теорема синусов:

Ты нашел то, что искал? Поделись с друзьями!

. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .

Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .

Запишем площадь треугольника АВС двумя способами:

Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .

В ответ запишем .

. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.

По теореме синусов,

Получаем, что . Угол — тупой. Значит, он равен .

. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.

Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.

, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем . Тогда .

Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .

📽️ Видео

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Математика за минуту: Объяснение формулы радиуса вписанной окружности в прямоугольный треугольник.Скачать

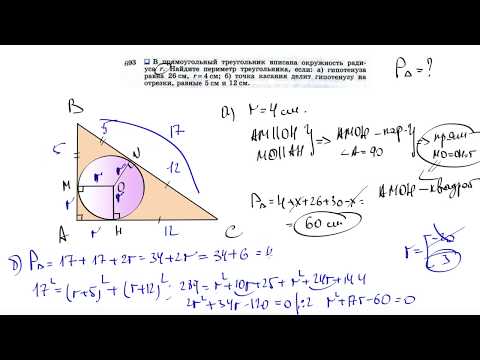
№693. В прямоугольный треугольник вписана окружность радиуса r. Найдите периметр треугольника,Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Окружность вписана в равносторонний треугольник, найти радиусСкачать

№703. В окружность вписан равнобедренный треугольник ABC с основанием ВС. Найдите углы треугольникаСкачать

Как разделить окружность на 3 равные части или как вписать равнобедренный треугольник в окружностьСкачать

Как поделить окружность на 3 равные части. Очень просто. Уроки черчения.Скачать

Треугольник, вписанный в окружность геометрия 7 классСкачать

Построить описанную окружность (Задача 1)Скачать

№702. В окружность вписан треугольник ABC так, что АВ — диаметр окружности. Найдите углыСкачать

15 задание треугольники огэ по математике / маттаймСкачать

Изогонали угла. Радиус описанной окружности и высота, проведенные из одной вершины треугольника.Скачать