В окружность радиуса 10 вписан равнобедренный треугольник высота треугольника

Определение: окружность называется описанной около четырёхугольника, >>

Задача: в окружность, радиус которой 10 см, вписан равнобедренный треугольник. Высота, проведённая к его основанию равна 16 см. Найти боковую сторону и площадь треугольника. Решение: Т. к. окружность описана около равнобедренного треугольника АВС, то центр окружности лежит на высоте ВН. АО = ВО = СО = 10 см, ОН = ВН – ВО = = 16 – 10 = 6 (см). АС = 2АН = 2 · 8 = 16 (см), SАВС = ? АС · ВН = ? · 16 · 16 = 128 (см2).

Слайд 6 из презентации «Описанная окружность»

Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Описанная окружность.ppt» можно в zip-архиве размером 97 КБ.

Вписанная и описанная окружность

«Вписанная окружность» — 2) Не во всякий четырехугольник можно вписать окружность. В любом описанном четырехугольнике суммы противоположных сторон равны. Доказательство: Замечания: Теорема: В любой треугольник можно вписать окружность. Задача № 1. Задача № 2. В треугольник можно вписать только одну окружность! Вписанная окружность.

«Описанная окружность» — Описанный многоугольник. Окружность. Многоугольник называется описанным около окружности, если … Окружность называется описанной около многоугольника, если… В любую ли фигуру можно вписать окружность? Как вписать описать нам окружность счастья? Треугольники и окружность. Что такое окружность? Вписанный многоугольник.

«Вписанная и описанная окружность» — При увеличении числа сторон правильного многоугольника угол многоугольника увеличивается. Древние математики не владели понятиями математического анализа. Мы можем ответить на проблемные вопросы. Круг. Окружность, описанная около правильного многоугольника, вписанная в правильный многоугольник. Мои исследования:

«Задачи на вписанную окружность» — Готовые чертежи. Радиус. Вписанная окружность. Художник. Центр вписанной в треугольник окружности. Полупериметр. Чёрный ящик. Капитан. Полупериметр многоугольника. Вписанные окружности. Возможные ответы. Конкурс капитанов. Тесты. Циркуль. Решение.

«Задачи по вписанной и описанной окружности» — Какой многоугольник называется вписанным. Какая окружность называется описанной. Сторона правильного шестиугольника. Можно ли описать окружность около правильного многоугольника. Найдите углы. Всегда ли можно ли описать окружность. Укажите центр окружности, описанной около трапеции. Найдите угол D. Около всякого треугольника можно описать окружность.

«Радиус вписанной и описанной окружности» — Описанная окружность. Окружность и треугольники. Выпуклый многоугольник. Описанная окружность около четырёхугольника. Вписанные и описанные окружности. Окружность. Основные формулы для правильных многоугольников. Трапеция. Вписанная окружность. Вписанная окружность в четырёхугольник. Окружность и прямоугольный треугольник.

В окружность радиуса 10 вписан равнобедренный треугольник?

Математика | 5 — 9 классы

В окружность радиуса 10 вписан равнобедренный треугольник.

Высота треугольника, проведенная к основанию, в сумме

с основанием дает диаметр окружности.

Найдите основание треугольника.

Рисуем треугольник АВС, где АС = 24 см и АВ = ВС.

Проводим высоту ВК = 9 см

S = 24 * 9 / 2 = 108 кв.

По свойствам равнобедренного треугольника

АК = КС = АС / 2 = 24 / 2 = 12 см

По теореме ПИфагора

АВ ^ 2 = ВК ^ 2 + AK ^ 2 = 9 ^ 2 + 12 ^ 2 = 81 + 144 = 225 = 15 ^ 2

р = (АВ + ВС + АС) / 2 = (15 + 15 + 24) / 2 = 27 см

Радиус вписанной окружности

r = S / p = 108 / 27 = 4 см

Синус угла А = ВК / АВ = 9 / 15 = 0, 6

Радиус описанной окружности

R = ВС / (2 * синус А) = 15 / (2 * 0, 6) = 12, 5 см проверь.

Основание равнобедренного треугольника 24 см , а высота опущенная на основание 9 см ?

Основание равнобедренного треугольника 24 см , а высота опущенная на основание 9 см .

Найти радиус вписанной окружности и описаннай окружности ))ПОЖАЛУЙСТА СРОЧНО НУЖНО!

Площадь равнобедренного треугольника равна 60см2 а основание 10см?

Площадь равнобедренного треугольника равна 60см2 а основание 10см.

Найдите радиус в треугольник окружности.

Боковые грани равнобедренного треугольника равны 5, основание равно 6?

Боковые грани равнобедренного треугольника равны 5, основание равно 6.

Найдите радиус вписанной окружности.

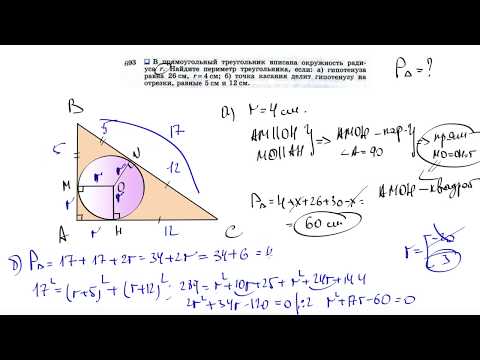
Высота, проведённая к основанию равнобедренного треугольника, равна 10, а высота, проведённая к боковой стороне, равна 12?

Высота, проведённая к основанию равнобедренного треугольника, равна 10, а высота, проведённая к боковой стороне, равна 12.

Найти радиус окружности, вписанной в треугольник.

Высота, проведённая к основанию равнобедренного треугольника, равна 18 см, а само основание павно 48 см?

Высота, проведённая к основанию равнобедренного треугольника, равна 18 см, а само основание павно 48 см.

Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.

В равнобедренном треугольнике основание равно 9 см, а боковая сторона равна 5см?

В равнобедренном треугольнике основание равно 9 см, а боковая сторона равна 5см.

Найдите радиус окружности вписанный в этот треугольник.

Равнобедренный треугольник с высотой, проведенной к основанию и равной 16см, вписан в окружность радиуса 10см?

Равнобедренный треугольник с высотой, проведенной к основанию и равной 16см, вписан в окружность радиуса 10см.

Найдите площадь этого треугольника и его боковую сторону.

В равнобедренном треугольнике с основание 40 см вписана окружность?

В равнобедренном треугольнике с основание 40 см вписана окружность.

Высота проведенная к основанию равна 15 см.

Найдите расстояние между точками касания окружности с боковыми сторонами треугольника.

Нужно записать последовательные логические действия и их обьяснение.

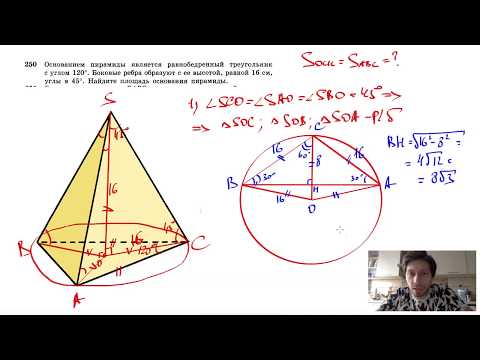
В равнобедренном треугольнике, основание равно 10 см?

В равнобедренном треугольнике, основание равно 10 см.

А высота проведенная к нему равна 12 см.

Найдите радиус окружности вписанной в этот треугольник и радиус окружности описанной около этого треугольника.

В окружность, радиус которой равен 8, вписан равнобедренный треугольник?

В окружность, радиус которой равен 8, вписан равнобедренный треугольник.

Угол при основании треугольника равен 75 градусам.

Найдите площадь треугольника.

Вы открыли страницу вопроса В окружность радиуса 10 вписан равнобедренный треугольник?. Он относится к категории Математика. Уровень сложности вопроса – для учащихся 5 — 9 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Математика, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

Он спрятал в второй норке 45.

84 — 39 = 45 (горошин) — во второй норке.

Качество прекрасное, если правильно разглядела, то : 1) — 3( — 5 + 5х) + 3х = — 6 15 — 15х + 3х = — 6 — 12х = — 21 х = 21 / 12 х = 1, 75 2) 4 — 9( — 5 + 9х) = — 10х — 9 4 + 45 — 81х = — 10х — 9 — 71х = — 58 х = 58 / 71 3) 7х + 2( — 7 + 5х) = — 8х — 2..

5х — 18 = 7х + 12 переносим х и обычные числа 5х — 7х = 18 + 12 — 2х = 30 сокращаем — х = 15 х = — 15.

5x — 18 = 7x + 12 5x — 7x = 12 + 18 — 2x = 30 x = 30 / — 2 x = — 15.

29 (целое число — это все натуральные числа, все противоположные им по знаку и ноль.

29 чисел. От — 14 до 0 14 чисел и от 0 до 14 — 14 чисел. Ну и 0.

Радиус вписанной окружности в равнобедренный треугольник онлайн

С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности, в том числе радиус вписанной в равнобедренный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Открыть онлайн калькулятор

1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона

Пусть известны известны основание a и боковая сторона b равнобедренного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной окружности через основание и боковую сторону.

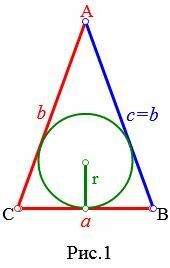Радиус вписанной в треугольник окружности через три стороны a, b, c вычисляется из следующей формулы:

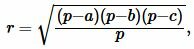(1)

где полупериметр p вычисляется из формулы:

.

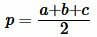(2)

Учитывая, что у равнобедренного треугольника боковые стороны равны (( small b=c )), имеем:

( small p=frac ) ( small =frac, )

(3)

( small p-a=frac-a ) ( small =frac, )

(4)

( small p-b=p-c=frac-b ) ( small =frac. )

(5)

Подставляя (3)-(5) в (1), получим формулу вычисления радиуса вписанной в равнобедренный треугольник окружности:

,

.

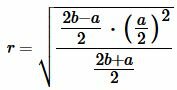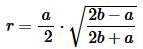(6)

Пример 1. Известны основание a=13 и боковая сторона b=7 равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значения ( small a,; b ) в (6):

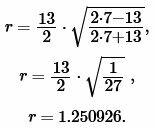Ответ:

2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании

Пусть известны основание a и прилежащий к ней угол β равнобедренного треугольника (Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.

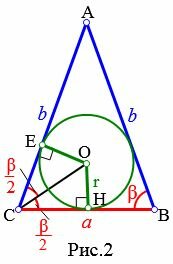Из центра вписанной окружности проведем перпендикуляры OH и OE к сторонам a=BC и b=AC, соответственно (r=OH=OE). Соединим точки C и O. Полученные прямоугольные треугольники OCE и OCH равны по гипотенузе и катету (см. статью Прямоугольный треугольник. Тогда ( small angle OCE=angle OCH=frac. ) Для прямоугольного треугольника OCH можно записать:

( small frac=frac<large frac>=mathrmfrac .)

Откуда получим формулу радиуса вписанной в треугольник окружности:

( small r=frac cdot mathrmfrac .)

(8)

( small r=frac cdot frac .)

(9)

Пример 2. Известны основание ( small a=15 ) и ( small beta=30° ) равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанный в треугольник воспользуемся формулой (8) (или (9)). Подставим значения ( small a=15, ; beta=30° ) в (8):

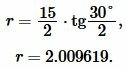Ответ:

3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании

Пусть известны боковая сторона b и угол при основании β равнобедренного треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.

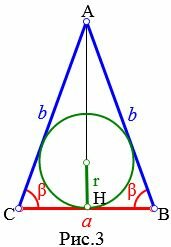Высота равнобедренного треугольника AH делит равнобедренный треугольник ABC на две равные части. Тогда для треугольника AHC справедливо равенство:

( small frac=frac<large frac>= cos beta .)

( small a=2b cdot cos beta .)

(10)

Подставляя (10) в (8), получим формулу вписанной в равнобедренный треугольник окружности:

( small r=frac cdot mathrmfrac=frac cdot mathrmfrac ) ( small =b cos beta cdot mathrmfrac )

( small r=b cdot cos beta cdot mathrmfrac )

(11)

Учитывая формулы половинного угла тригонометрических функций, формулу (11) можно записать и так:

( small r=b cdot frac )

(12)

Пример 3. Известны боковая сторона равнобедренного треугольника: ( small b=9 ) и угол при основании β=35°. Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11) (или (12)).

Подставим значения ( small b=9 ,; beta=35° ) в (11):

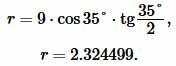Ответ:

4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота

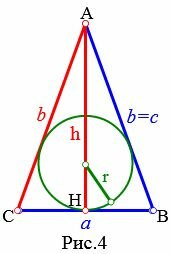
Пусть известны боковая сторона b и высота h равнобедренного треугольника (Рис.4). Найдем формулу радиуса вписанной в треугольник окружности.

Формула радиуса вписанной окружности через площадь и полупериметр имеет следующий вид (см. статью на странице Радиус вписанной в треугольник окружности онлайн) :

,

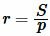(13)

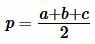(14)

Так как треугольник AHC прямоугольный, то из Теоремы Пифагора имеем:

( small left( fracright)^2=b^2-h^2 )

( small a=2 cdot sqrt )

(15)

Площадь равнобедренного треугольника по основанию и высоте вычисляется из формулы:

( small S=frac cdot a cdot h. )

(16)

Подставим (15) в (16):

( small S=h cdot sqrt )

(17)

Учитывая, что для равнобедренного треугольника b=c, а также равенство (15), получим:

( small p=frac ) ( small =frac ) ( small =frac+b )( small =b+ sqrt )

(18)

Подставляя, наконец, (17) и (18) в (13), получим формулу радиуса вписанной в равнобедренный треугольник окружности:

( small r=frac ) ( small =frac<large h cdot sqrt><large b+ sqrt> )

(19)

Пример 4. Боковая сторона и высота равнобедренного треугольника равны ( small b=7 ,) ( small h=5, ) соответственно. Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (19). Подставим значения ( small b=7 ,) ( small h=5 ) в (19):

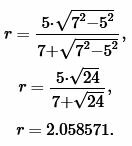Ответ:

5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота

Пусть известны основание a и высота h равнобедренного треугольника (Рис.5). Найдем формулу радиуса вписанной в равнобедренный треугольник окружности.

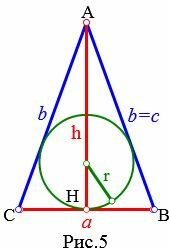Из формулы (15) найдем b:

( small b^2-h^2=left( frac right)^2 )

( small b^2= frac +h^2 )

( small b= frac cdot sqrt)

(20)

Подставляя (20) в (19), получим формулу радиуса вписанной окружности в равнобедренный треугольник:

( small r=frac<large h cdot sqrt><large b+ sqrt>) ( small =frac<large h cdot sqrt<frac+h^2-h^2>><large frac cdot sqrt+ sqrt<frac+h^2-h^2>>) ( small = large frac< h cdot frac>< frac cdot sqrt+frac >)

( small r=large frac<a+ sqrt>)

(21)

Пример 5. Основание и высота равнобедренного треугольника равны ( small a=7 ,) ( small h=9, ) соответственно. Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (21). Подставим значения ( small a=7 ,) ( small h=9 ) в (21):

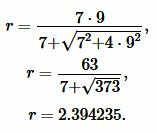Ответ:

🎥 Видео