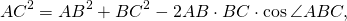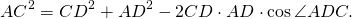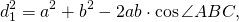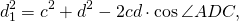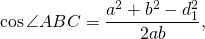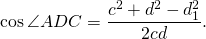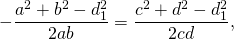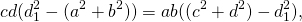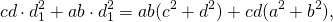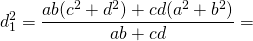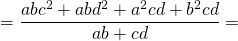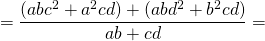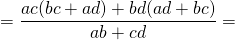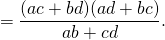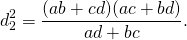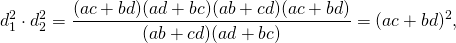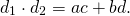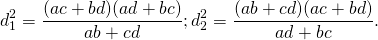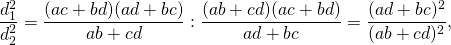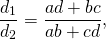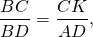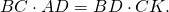Вписанные четырехугольники и их свойства Вписанные четырехугольники и их свойства |
 Теорема Птолемея Теорема Птолемея |
- Вписанные четырёхугольники и их свойства
- Теорема Птолемея
- В любом четырехугольнике вписанном в окружность произведение диагоналей
- Четырехугольники, вписанные в окружность. Теорема Птолемея
- Вписанные четырёхугольники и их свойства
- Теорема Птолемея
- Теорема Птолемея
- Многоугольник. Нахождение диагоналей вписанного четырехугольника. Теорема Птоломея.
- Многоугольник. Нахождение диагоналей вписанного четырехугольника. Теорема Птоломея.
- 💡 Видео
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Вписанные четырёхугольники и их свойства
Определение 1 . Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником .
Теорема 1 . Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180° .
Доказательство . Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC . Угол ADC является вписанным углом, опирающимся на дугу ABC . Поэтому величина угла ADC равна половине угловой величины дуги ABC . Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180° .
Если рассмотреть углы BCD и BAD , то рассуждение будет аналогичным.
Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1) . Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.
Доказательство . Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A , B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D . Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).
Продолжим отрезок CD за точку D до пересечения с окружностью в точке E , и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180° . При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC . Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC , не смежного с ним.
Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.
Теорема 2 доказана.
Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.
| Фигура | Рисунок | Свойство | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около параллелограмма |  | Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около ромба |  | Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около трапеции |  | Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около дельтоида |  | Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Произвольный вписанный четырёхугольник |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около параллелограмма | ||||||||||||||||||||||||||||||||||||||||||||||||||||
 | Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. | |||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около ромба | ||||||||||||||||||||||||||||||||||||||||||||||||||||
 | Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. | |||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около трапеции | ||||||||||||||||||||||||||||||||||||||||||||||||||||
 | Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. | |||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около дельтоида | ||||||||||||||||||||||||||||||||||||||||||||||||||||
 | Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. | |||||||||||||||||||||||||||||||||||||||||||||||||||
| Произвольный вписанный четырёхугольник | ||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около параллелограмма |
 |
Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.

Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.

Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.

Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:
где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.
Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

Теорема Птолемея
Теорема Птолемея . Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.
Доказательство . Рассмотрим произвольный четырёхугольник ABCD , вписанный в окружность (рис.3).
Докажем, что справедливо равенство:
Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).
Заметим, что треугольник ABD подобен треугольнику BCE . Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E ), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
откуда вытекает равенство:
 | (1) |
Заметим, что треугольник ABE подобен треугольнику BCD . Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
Видео:3 правила для вписанного четырехугольника #shortsСкачать

В любом четырехугольнике вписанном в окружность произведение диагоналей
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Четырехугольники, вписанные в окружность. Теорема Птолемея
 Вписанные четырехугольники и их свойства Вписанные четырехугольники и их свойства |
 Теорема Птолемея Теорема Птолемея |
Видео:Вписанные четырехугольники. 9 класс.Скачать

Вписанные четырёхугольники и их свойства
Определение 1 . Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником .
Теорема 1 . Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180° .
Доказательство . Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC . Угол ADC является вписанным углом, опирающимся на дугу ABC . Поэтому величина угла ADC равна половине угловой величины дуги ABC . Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180° .
Если рассмотреть углы BCD и BAD , то рассуждение будет аналогичным.
Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1) . Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.
Доказательство . Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A , B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D . Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).
Продолжим отрезок CD за точку D до пересечения с окружностью в точке E , и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180° . При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC . Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC , не смежного с ним.
Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.
Теорема 2 доказана.
Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.
| Фигура | Рисунок | Свойство | ||||||||||||||||||||||||||||||
| Окружность, описанная около параллелограмма |  | Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. | ||||||||||||||||||||||||||||||
| Окружность, описанная около ромба |  | Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. | ||||||||||||||||||||||||||||||
| Окружность, описанная около трапеции |  | Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. | ||||||||||||||||||||||||||||||
| Окружность, описанная около дельтоида |  | Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. | ||||||||||||||||||||||||||||||
| Произвольный вписанный четырёхугольник |  | |||||||||||||||||||||||||||||||
| Окружность, описанная около параллелограмма | ||
 | Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. | |
| Окружность, описанная около ромба | ||
 | Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. | |
| Окружность, описанная около трапеции | ||
 | Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. | |
| Окружность, описанная около дельтоида | ||
 | Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. | |
| Произвольный вписанный четырёхугольник | ||
 | ||
| Окружность, описанная около параллелограмма |
 |
Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.

Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.

Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.

Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:
где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Теорема Птолемея
Теорема Птолемея . Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.
Доказательство . Рассмотрим произвольный четырёхугольник ABCD , вписанный в окружность (рис.3).
Докажем, что справедливо равенство:
Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).
Заметим, что треугольник ABD подобен треугольнику BCE . Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E ), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
откуда вытекает равенство:
 | (1) |
Заметим, что треугольник ABE подобен треугольнику BCD . Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
Видео:Вписанный в окружность четырёхугольник.Скачать

Теорема Птолемея
Произведение диагоналей вписанного четырёхугольника равно сумме произведений двух пар его противолежащих сторон.
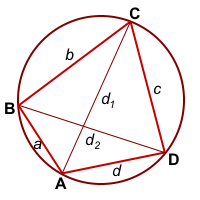
4-угольник ABCD вписан в окр. (O; R)
Из треугольников ABC и ADC по теореме косинусов
Введём обозначения AB=a, BC=b, CD=c, AD=d, AC=d1, BC=d2.
Так как четырёхугольник ABCD — вписанный, то ∠ABC+∠ADC=180°.
Что и требовалось доказать.
В ходе доказательства получили полезные соотношения:
1) Диагонали вписанного четырёхугольника связаны с его сторонами равенствами:
2)Отношение диагоналей вписанного четырёхугольника.
то есть диагонали вписанного четырехугольника относятся как суммы произведений сторон, сходящихся в концах диагоналей.
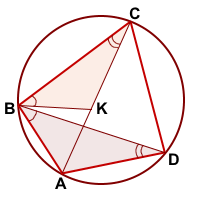
У треугольников CBK и DBA
∠CBK=∠DBA (по построению)
Значит треугольники CBK и DBA подобны (по двум углам).
Из подобия треугольников следует пропорциональность соответствующих сторон:
откуда по основному свойству пропорции
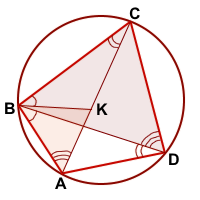
∠BAK=∠BDC (как вписанные углы, опирающиеся на одну дугу BC).
а так как ∠ABD=∠CBK, то и ∠ABK=∠DBC.
Следовательно, треугольники ABK и DBC подобны (по двум углам), и
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Многоугольник. Нахождение диагоналей вписанного четырехугольника. Теорема Птоломея.
Обозначим стороны вписанного четырехугольника ABCD через a, b, с, d и его диагонали через x и y .Проведем AK ^ BС и СL ^ AD.
Так как сумма противоположных углов вписанного четырехугольника равна 2d, то, если угол B острый, угол D должен быть тупым.
Поэтому из треугольников ABС и ADС можем написать:
x 2 = a 2 + b 2 – 2b . BK [1];
x 2 = с 2 + d 2 + 2d . DL [2].
Прямоугольные треугольники ABK и СDL подобны, т.к. они содержат по равному острому углу (углы B и СDL равны, потому что каждый из них служит дополнением до 2d к углу ADС).
Из их подобия выводим:
откуда BK . с = DL . a [3].
Таким образом, мы получим три уравнения с тремя неизвестными x, BK и DL.
Чтобы исключить BK и DL , уравняем в первых двух уравнениях последние члены, для чего умножим уравнение [1] на сd , а уравнение [2] на ab .
Сложив затем результаты и, приняв во внимание уравнение [3], найдем:
(ab + сd)x 2 = a 2 сd + b 2 сd + с 2 ab + d 2 ab =aс(ad + bс) + bd(bс+ad)=(aс + bd)(ad+bс),
.
Заметим, что в числителе подкоренной величины первый множитель — сумма произведений противоположных сторон, а второй — сумма произведений сторон, сходящихся в концах определяемой диагонали, знаменатель же представляет сумму произведений сторон, сходящихся в концах другой диагонали.
После этого мы можем, по аналогии, написать следующую формулу для диагонали y:
.
Следствие 1.
Произведение диагоналей вписанного четырехугольника равно сумме произведений противоположных сторон.
Действительно, перемножив выражения, выведенные для x и для y, получим:
.
Это предложение известно под именем теоремы Птоломея.
Следствие 2.
Отношение диагоналей вписанного четырехугольника равно отношению суммы произведений сторон, сходящихся в концах первой диагонали, к сумме произведений сторон, сходящихся в концах второй диагонали.
Действительно, разделив те же два равенства, найдем:
.
Эти два следствия удобны для запоминания. Из них можно обратно вывести формулы для x и y (перемножением или делением равенств, определяющих xy и x/y).
Видео:Вписанный четырёхугольник | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис ТрушинСкачать

Многоугольник. Нахождение диагоналей вписанного четырехугольника. Теорема Птоломея.
Обозначим стороны вписанного четырехугольника ABCD через a, b, с, d и его диагонали через x и y .Проведем AK ^ BС и СL ^ AD.
Так как сумма противоположных углов вписанного четырехугольника равна 2d, то, если угол B острый, угол D должен быть тупым.
Поэтому из треугольников ABС и ADС можем написать:
x 2 = a 2 + b 2 – 2b . BK [1];
x 2 = с 2 + d 2 + 2d . DL [2].
Прямоугольные треугольники ABK и СDL подобны, т.к. они содержат по равному острому углу (углы B и СDL равны, потому что каждый из них служит дополнением до 2d к углу ADС).
Из их подобия выводим:
откуда BK . с = DL . a [3].
Таким образом, мы получим три уравнения с тремя неизвестными x, BK и DL.
Чтобы исключить BK и DL , уравняем в первых двух уравнениях последние члены, для чего умножим уравнение [1] на сd , а уравнение [2] на ab .
Сложив затем результаты и, приняв во внимание уравнение [3], найдем:
(ab + сd)x 2 = a 2 сd + b 2 сd + с 2 ab + d 2 ab =aс(ad + bс) + bd(bс+ad)=(aс + bd)(ad+bс),
.
Заметим, что в числителе подкоренной величины первый множитель — сумма произведений противоположных сторон, а второй — сумма произведений сторон, сходящихся в концах определяемой диагонали, знаменатель же представляет сумму произведений сторон, сходящихся в концах другой диагонали.
После этого мы можем, по аналогии, написать следующую формулу для диагонали y:
.
Следствие 1.
Произведение диагоналей вписанного четырехугольника равно сумме произведений противоположных сторон.
Действительно, перемножив выражения, выведенные для x и для y, получим:
.
Это предложение известно под именем теоремы Птоломея.
Следствие 2.
Отношение диагоналей вписанного четырехугольника равно отношению суммы произведений сторон, сходящихся в концах первой диагонали, к сумме произведений сторон, сходящихся в концах второй диагонали.
Действительно, разделив те же два равенства, найдем:
.
Эти два следствия удобны для запоминания. Из них можно обратно вывести формулы для x и y (перемножением или делением равенств, определяющих xy и x/y).
💡 Видео
11 класс, 43 урок, Вписанный четырехугольникСкачать

#58. Олимпиадная задача о четырехугольникеСкачать

2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать

Углы, вписанные в окружность. 9 класс.Скачать

Вписанные углы в окружностиСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

ОПИСАННЫЕ И ВПИСАННЫЕ ОКРУЖНОСТИ ЧЕТЫРЕХУГОЛЬНИКА . §10 геометрия 8 классСкачать

8 класс Геометрия. Окружность вписанная в четырехугольник и описанная около четырехугольника Урок #4Скачать

Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать

Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

Свойство и признак вписанного четырехугольникаСкачать