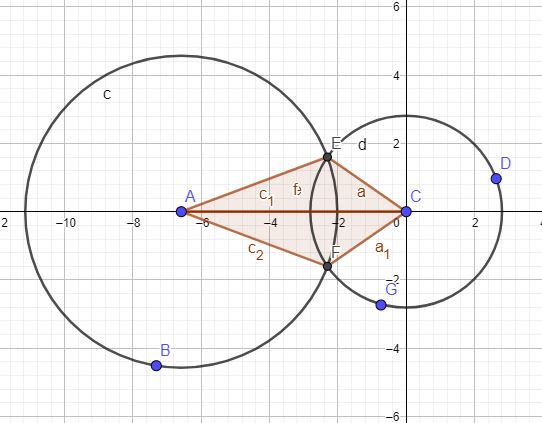
Даны две окружности, каждая определена координатами своего центра и радиусом. Требуется найти все их точки пересечения (либо одна, либо две, либо ни одной точки, либо окружности совпадают).
Видео:Теорема о числе точек пересечения двух окружностейСкачать

Решение
Предположим, не теряя общности, что центр первой окружности — в начале координат (если это не так, то перенесём центр в начало координат, а при выводе ответа будем обратно прибавлять координаты центра). Тогда мы имеем систему двух уравнений:
Вычтем из второго уравнения первое, чтобы избавиться от квадратов переменных:
Таким образом, мы свели задачу о пересечении двух окружностей к задаче о пересечении первой окружности и следующей прямой:
А решение последней задачи описано в соответствующей статье.
Единственный вырожденный случай, который надо рассмотреть отдельно — когда центры окружностей совпадают. Действительно, в этом случае вместо уравнения прямой мы получим уравнение вида 0 = С, где C — некоторое число, и этот случай будет обрабатываться некорректно. Поэтому этот случай нужно рассмотреть отдельно: если радиусы окружностей совпадают, то ответ — бесконечность, иначе — точек пересечения нет.
Видео:Алгоритмы. Пересечение окружностейСкачать

Пересечение двух окружностей
Этот онлайн калькулятор находит точки пересечения двух окружностей, если они существуют
Чтобы использовать калькулятор, введите координаты x и y центра и радиус каждой окружности.
Формулы для расчета приведены под калькулятором.
Точки пересечения двух окружностей
Первая окружность
Вторая окружность
Видео:Пересечение двух окружностейСкачать

Пересечение окружностей
Сама по себе задача нахождения точек пересечения двух окружностей достаточно проста, однако предварительно надо проанализировать если ли вообще точки пересения у данных двух окружностей. Поэтому начать надо с вычисления расстояния d в декартовых координатах между центрами окружностей и сравнения его с радиусами окружностей r1 и r2.
При этом возможно следующие случаи (расстояние между центрами показано красным отрезком):
| Случай | Описание | Условие |
|---|---|---|
| Тривиальный случай — окружности совпадают (это одна и та же окружность) | ||
| Окружности не касаются друг друга | r1 + r2″ /> | |
| Одна окружность содержится внутри другой и не касается ее | ||
| Окружности пересекаются в двух точках | Не выполнено ни одно из условий выше | |
| Окружности соприкасаются в одной точке | Частный случай предыдущего |
Если окружности действительно пересекаются, калькулятор использует следующие формулы (в-основном выведенные из теоремы Пифагора), проиллюстрированные рисунком ниже:
Сначала калькулятор находит отрезок a
Чтобы найти точку P3, калькулятор использует следующую формулу (в векторном виде):
И наконец, чтобы найти точки пересечения, калькулятор использует следующие уравнения:
Первая точка:
Обратите внимание на разные знаки перед вторым слагаемым
По теме также можно посмотреть следующие ссылки (на английском языке): Circle-Circle Intersection и Circles and spheres
Видео:Пересечение двух окружностейСкачать

Координаты пересечения двух окружностей
| Координаты центра первой окружности, через пробел |
| Радиус первой окружности |
| Координаты центра второй окружности, через пробел |
| Радиус второй окружности |
| Координата первого пересечения |
| Координата второго пересечения |
Продолжим изучение геометрии и в этом материале мы рассмотрим, как находить координаты пересечения двух окружностей, если заданы их уравнения. Определение координат двух окружностей на плоскости можно свести к более простым задачам которые мы можем уже решать или понимаем, как их решать. Пусть Две окружности заданы своими двумя уравнениями Повернем изображение на такой угол, что бы линия соединяющая центры окружностей, совпадала с осью абсцисс. Кроме этого перенесем всю схему таким образом, что бы центр одной из окружностей совпал с началом координат.
И алгоритм следующий: 1. Приводим ( линейным смещением) центр первой окружности к координатам (0,0) 3. Определяем угол (W) прямой, проходящей между точками A и C 4. Определяем два угла (psi_1) как сумму и (psi_2) как разность углов W и F 5. Взяв для каждого из углов (в п. 4), синус и умножив на радиус первой окружности мы узнаем координату Y , взяв косинус мы узнаем координату X. 6. Делаем для двух полученных координат, обратное смещение. 🎥 ВидеоВзаимное расположение окружностей. Точки пересечения окружностейСкачать  Точка пересечения двух окружностей равноудалена ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать  Две окружности на плоскости. Математика. 6 класс.Скачать  Точка встречи прямой с плоскостьюСкачать  Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать  Пересечение двух окружностейСкачать  9 класс, 8 урок, Взаимное расположение двух окружностейСкачать  Геометрия Докажите, что прямая, проходящая через точки пересечения двух окружностей, делит пополамСкачать  Взаимное расположение окружностей. 7 класс.Скачать  Геометрия 9 класс (Урок№10 - Взаимное расположение двух окружностей.)Скачать  1 2 4 сопряжение окружностейСкачать  Точки пересечения графиков линейных функций. 7 класс.ОбразовательныйСкачать  Линия пересечения двух поверхностей вращения (Метод вспомогательных сфер)Скачать  Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать  Геометрия В точках пересечения двух окружностей с радиусами 4 и 8 см касательные к ним взаимноСкачать  Пересечения прямых, лучей, отрезковСкачать  |







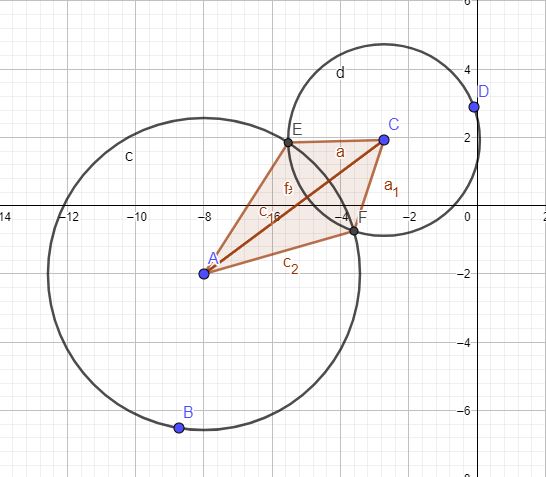
 Теперь мы можем решить данную задачу по несложной формуле.
Теперь мы можем решить данную задачу по несложной формуле.