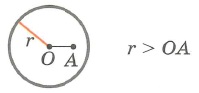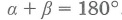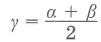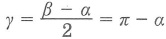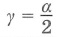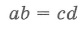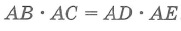Метрические соотношения в окружности

Отрезки и прямые, связанные с окружностью

Свойства хорд и дуг окружности

Теоремы о длинах хорд, касательных и секущих

Доказательства теорем о длинах хорд, касательных и секущих

Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках

Фигура	Рисунок	Определение и свойства
Окружность
Круг
Радиус
Хорда
Диаметр
Касательная
Секущая

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды		Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности		Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Фигура	Рисунок	Теорема
Пересекающиеся хорды
Касательные, проведённые к окружности из одной точки
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Пересекающиеся хорды

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Тогда справедливо равенство

Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.

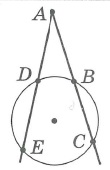
Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).

Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

Теорема о бабочке

Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:

Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим

Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим

Воспользовавшись теоремой 1, получим

Воспользовавшись равенствами (1) и (2), получим

Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство

откуда вытекает равенство

что и завершает доказательство теоремы о бабочке.

Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности

Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью.
Взаимное расположение окружности и прямой, окружности и точки, двух окружностей.
Свойства углов, связанных с окружностью. Метрические соотношения в окружности.

Прямые, отрезки и углы, связанные с окружностью:

Центральный угол измеряется дугой, на которую он опирается. Если отнести длину этой дуги к радиусу окружности то получится радианная мера угла.

Взаимное расположение окружности и прямой:

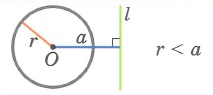
1. Окружность и прямая не имеют общих точек

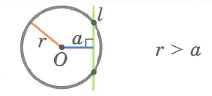
2. Окружность и прямая имеют 2 общие точки (l — секущая)

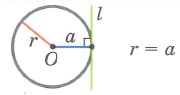
3. Окружность и прямая имеют 1 общую точку (l — касательная)

Взаимное расположение окружности и точки:

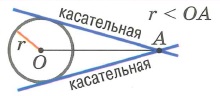
1. Точка лежит вне окружности (2 касательные через точку А)

2. Точка лежит внутри окружности (нет касательных через точку А)

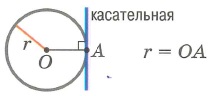
3. Точка лежит на окружности (1 касательная через точку А)

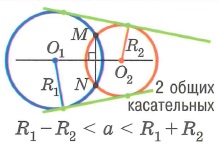
Взаимное расположение двух окружностей:

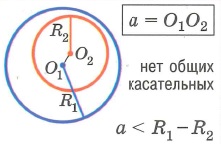
1. Одна окружность лежит внутри другой.

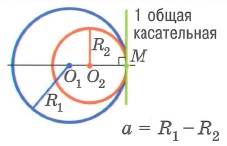
2. Одна окружность касается другой изнутри.

3. Окружности пересекаются.

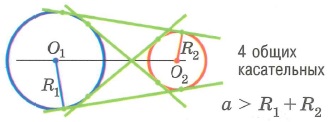
4. Одна окружность касается другой снаружи или одна окружность лежит вне другой.

Свойства углов, связанных с окружностью:

Вписанный угол равен половине центрального, опирающегося на ту же дугу:

Все вписанные углы, опирающиеся на одну и ту же дугу равны:Все вписанные углы, опирающиеся на одну и ту же хорду, вершины которых лежат по одну сторону от этой хорды, равны:

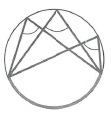
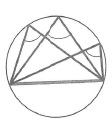
Любые два вписанных угла, опирающиеся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 180°=π

Все вписанные углы, опирающиеся на диаметр, прямые:

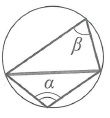
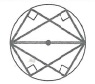
Угол между пересекающимися хордами:

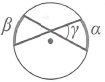
Угол между секущими, пересекающимися вне окружности:

Угол между касательной и секущей:

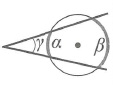
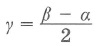
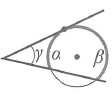
Угол между касательными:

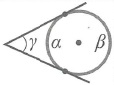
Угол между касательной и хордой:

Метрические соотношения в окружности (длины отрезков):

Отрезки пересекающихся хорд связаны соотношением:

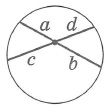
Отрезки касательных, проведенных из общей точки, равны:

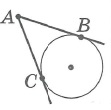
Квадрат длины отрезка касательной равен произведению длин отрезков секущей, проведенной из той же точки:

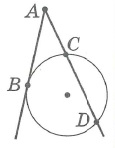
Произведения длин отрезков секущих, проведенных из общей точки, равны:

Консультации и техническая
поддержка сайта: Zavarka Team

Геометрия треугольника и окружности (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5

ГЕОМЕТРИЯ ТРЕУГОЛЬНИКА И ОКРУЖНОСТИ

Начнем с перечня «рабочих» теорем.

1. Свойства касательных к окружности:

а) радиус, проведенный в точку касания, перпендикулярен касательной (рис. 1);

б) две касательные, проведенные к окружности из одной точки, равны, и центр окружности лежит на биссектрисе угла между ними (рис. 2).

2. Измерение углов, связанных с окружностью:

а) центральный угол измеряется дугой, на которую он опирается (рис.3);

б) вписанный угол измеряется половиной дуги, на которую он опирается (рис. 4);

в) угол между касательной и хордой измеряется половиной дуги, заключенной между касательной и хордой (рис.5).

3. Теоремы об окружностях и треугольниках:

а) около всякого треугольника можно описать окружность; центром окружности служит точка пересечения перпендикуляров, проведенных к сторонам через их середины;

б) во всякий треугольник можно вписать окружность; центром окружности служит точка пересечения биссектрис.

4. Теоремы об окружностях и четырехугольниках:

а) для того чтобы около четырехугольника можно было описать окружность, необходимо и достаточно, чтобы сумма противолежащих углов четырехугольника была равна 180° (, рис.6);

б) для того чтобы в четырехугольник можно было вписать окружность, необходимо и достаточно, чтобы суммы противолежащих его сторон были равны ( рис. 7).

5. Метрические соотношения в окружности:

а) если хорды АВ и CD пересекаются в точке М, то AMBM = CMDM (рис. 8);

б) если из точки М к окружности проведены две секущие МАВ и MCD, то AM ВМ = СМ DM (рис. 9);

в) если из точки М к окружности проведены секущая МАВ и касательная МС, то АМВМ = СМ2 (рис. 10).

Начнем с рассмотрения ряда несложных задач, иллюстрирующих применение на практике перечисленных «рабочих» теорем.

Задача 1. Катеты прямоугольного треугольника а и b, гипотенуза с. Вычислим радиус r вписанной окружности.

Решение. 1. Из центра О вписанной окружности проведем радиусы в точки ее касания со сторонами треугольника, учитывая, что они перпендикулярны соответствующим сторонам (теорема 1, а), и отметим пары равных отрезков, воспользовавшись теоремой 1, б (рис.11).

3. Так как АВ =AF + FВ, то получаем с = (b – r) +(a –r), откуда .

Ответ: .

Замечание 1. Если в задаче речь идет об окружности, вписанной в треугольник (или четырехугольник), то практически всегда проводят радиусы в точки касания окружности со сторонами, учитывая, что радиусы будут перпендикулярны соответствующим сторонам, и тут же отмечают на чертеже пары равных отрезков (для двух касательных, проведенных к окружности из одной точки). Так мы и поступили при решении задачи 1.

Замечание 2. Обратите внимание на формулу для вычисления радиуса окружности, вписанной в прямоугольный (только прямоугольный) треугольник. Она довольно проста, ее легко запомнить, что мы вам и советуем сделать. Для непрямоугольного треугольника обычно используют формулу , где S – площадь, р – полупериметр треугольника.

Что касается радиуса R описанной около треугольника окружности, то для прямоугольного треугольника (гипотенуза является диаметром описанной около прямоугольного треугольника окружности); для непрямоугольного треугольника обычно используют формулы и . B правильном треугольнике со стороной а .

Замечание 3. До сих пор мы приводили только формулировки теорем, считая, что их доказательства при необходимости читатель найдет в школьных учебниках. С теоремой синусов поступим по-другому: приведем доказательство теоремы, тем более что оно отличается от традиционного «школьного» доказательства и достаточно красиво (см. задачу 2).

Задача 2. Докажем, что в треугольнике выполняется соотношение .

Решение. Пусть около треугольника ABC описана окружность радиуса R, проведем ее диаметр BD и соединим точку D с точкой С. (рис. 12).

Замечаем, что (как вписанные, опирающиеся на одну и ту же дугу ВС), BCD = 90° (как опирающийся на диаметр BD). Тогда из BCD находим: т. е. , откуда .

Задача 3. В равнобедренном треугольнике со сторонами 10, 10 и 12 вычислим радиусы вписанной (r) и описанной (R) окружностей.

Имеем: (мы воспользовались формулой Герона). Значит,

Пусть O1 – центр вписанной в треугольник AВС окружности – точка пересечения биссектрис ВН и АО1 (рис. 13). ВН одновременно является высотой и медианой треугольника ABC, . Применив к треугольнику АВН теорему о биссектрисе, получим , т. е. , откуда находим .

Пусть О1 – центр вписанной в треугольник ABC окружности, , тогда (рис.14). Из подобия треугольников О1КВ и АВН получаем , т. е. , откуда г = 3.

🎦 Видео