В кольце образованном двумя концентрическими окружностями

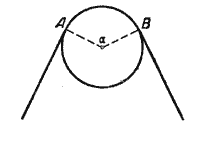
Вопрос по геометрии:

В кольце, образуемом двумя концентрическими окружностями, проведена хорда, касающаяся меньщей окружности. Найдите площадь кольца , если известно, что длина хорды равна 8 см.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

r^2+16=R^2 — из прямоугольного треугольника образованного хордой малым и большим радиусами по теореме Пифагора

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

В кольце, образуемом двумя концентрическими окружностями, проведена хорда, касающаяся меньщей окружности?

Геометрия | 10 — 11 классы

В кольце, образуемом двумя концентрическими окружностями, проведена хорда, касающаяся меньщей окружности.

Найдите площадь кольца , если известно, что длина хорды равна 8 см.

R ^ 2 + 16 = R ^ 2 — из прямоугольного треугольника образованного хордой малым и большим радиусами по теореме Пифагора

S = Pi (R ^ 2 — r ^ 2)

Видео:Геометрия Круг радиуса R разделен двумя концентрическими с ним окружностями на три равновеликиеСкачать

В окружности радиус которой равен 5, проведена хорда АВ = 8?

В окружности радиус которой равен 5, проведена хорда АВ = 8.

Точка С лежит на хорде АВ так что АС : ВС = 1 : 2.

Найдите радиус окружности касающейся данной окружности и касающейся хорды АВ в точке С.

Видео:2214 Найдите площадь кольца ограниченного концентрическими окружностямиСкачать

Найдите площадь кругового кольца, заключенного между двумя концентрическими окружностями, длины которых равны а и b, где а &lt ; b?

Найдите площадь кругового кольца, заключенного между двумя концентрическими окружностями, длины которых равны а и b, где а &lt ; b.

Видео:№1120. Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусамиСкачать

В окружности проведены три попарно пересекающиеся хорды равной длины?

В окружности проведены три попарно пересекающиеся хорды равной длины.

Каждая хорда разделена точками пересечения на три части равной длины.

Найти радиус окружности, если длина каждой из хорд равна а.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

В окружности проведены две взаимно перпендикулярные хорды?

В окружности проведены две взаимно перпендикулярные хорды.

Хорда, длина которой 10 , удалена от центра окружности на расстояние 3.

Найдите длину другой хорды, если известно, что она удалена от центра на расстояние 4.

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

В окружности проведены две взаимно перпендикулярные хорды?

В окружности проведены две взаимно перпендикулярные хорды.

Хорда, длина которой 10 , удалена от центра окружности на расстояние 4.

Найдите длину другой хорды, если известно, что она удалена от центра на расстояние 5.

Видео:9 класс, 26 урок, Длина окружностиСкачать

Из точки окружности проведены диаметр и хорда, длинна которой равна радиусу?

Из точки окружности проведены диаметр и хорда, длинна которой равна радиусу.

Найдите угол между хордой и диаметром.

Видео:6.2 Решение задач для уравнения Лапласа в круге, вне круга и в кольцеСкачать

Длина хорды окружности равна 26, а расстояние от центра окружности до этой хорды равно 10?

Длина хорды окружности равна 26, а расстояние от центра окружности до этой хорды равно 10.

Найдите диаметр окружности.

Видео:Длина окружности и площадь кругаСкачать

В окружности с диаметром 34 дм, проведена хорда, длина которой равна 30дм?

В окружности с диаметром 34 дм, проведена хорда, длина которой равна 30дм.

Найдите длину отрезка, соединяющего серидину хорды с центром окружности.

Видео:На окружности по разные стороны от диаметра AB ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

В окружности диаметр которой равен 50?

В окружности диаметр которой равен 50?

Что расстояние от центра окружности до этой хорды равно 15 / найдите длину этой хорды.

Видео:#59. Олимпиадная задача о касательной к окружности!Скачать

Длина хорды окружности равна 30, а расстояние от центра окружности до этой хорды равно 36?

Длина хорды окружности равна 30, а расстояние от центра окружности до этой хорды равно 36.

Найдите диаметр окружности.

Если вам необходимо получить ответ на вопрос В кольце, образуемом двумя концентрическими окружностями, проведена хорда, касающаяся меньщей окружности?, относящийся к уровню подготовки учащихся 10 — 11 классов, вы открыли нужную страницу. В категории Геометрия вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

Видео:Найдите площадь кольца ● 2Скачать

В кольце образованном двумя концентрическими окружностями

§ 15. Длина окружности и дуги. Площадь круга и его частей .

Длина окружности и дуги.

1. Вычислить длину окружности, если радиус равен: 1) 10 м; 2) 15 м; 3) 35 см.

2. Вычислить радиус, если длина окружности равна: 1) 1 м; 2) 25 см; 3) 4,75 дм.

3. Расстояние между серединами двух зубцов зубчатого колеса, имеющего 0,66 м в диаметре, равно 34,5 мм, считая по дуге. Сколько зубцов имеет колесо?

4. Шкив имеет в диаметре 1,4 м и делает 80 оборотов в минуту. Определить скорость точки, лежащей на окружности шкива.

5. По данному радиусу R определить длину дуги, содержащей:
1) 45°; 2) 24°30′; 3) 5°14’15».

6. Определить радиус дуги, если её длина равна l, а градусная мера: 1) 135°; 2) 1040′.

7. Окружность шкива (черт. 28) имеет длину 540 мм, ремень касается шкива по дуге длиной 200 мм. Определить угол обхвата шкива ремнём (α).

8. Радиус железнодорожного закругления равен 1200 м; длина дуги равна 450 м. Сколько градусов содержит дуга?

9. 1) Окружность радиуса 2 см разогнута в дугу радиуса 5 см. Найти получившийся центральный угол.

2) Дуга радиуса 4 см, измеряющая центральный угол в 120°, равна длине некоторой окружности. Найти радиус этой окружности.

3) Окружность радиуса 6 см разогнута в дугу, измеряющую центральный угол в 300°. Найти радиус дуги.

10. Определить число градусов дуги, если дан её ра диус R и длина l:
1) R = 10, l = 45; 2) R=15, l = 6.

11. Сколько градусов и минут в дуге, длина которой равна радиусу( 1 /_π = 0,31831)?

12. По данной хорде а определить длину её дуги, если она содержит:
1) 60°; 2) 90°; 3) 120°.

13. По данной длине дуги l определить её хорду, если дуга содержит:
1) 60°; 2) 90°; 3) 120°.

14. Определить радиус окружности, если она длиннее своего диаметра на 107 см.

15. 1) На сколько увеличится длина окружности, если радиус увеличится на m ?

2) Вообразим, что земной шар обтянут по экватору обручем и что подобным же образом обтянут и футбольный мяч по его большому кругу. Далее, вообразим, что окружность каждого обруча удлинилась на 1 м. Тогда обручи отстанут от поверхности тел, которые они раньше стягивали, и останется некоторый прозор (промежуток). В каком случае этот прозор был бы больше: у земного шара или мяча?

16. 1) Железная труба со стенками толщиной в 6 мм имеет внешнюю окружность в 22 см. Найти длину внутренней окружности.

2) Из двух концентрических окружностей одна равна 167 см, а другая 117 см. Определить ширину кольца.

17. Определить длину окружности, если она более периметра правильного вписанного шестиугольника на 7 см.

18. Дуга сегмента содержит 120° и имеет длину l. Определить длину окружности, вписанной в этот сегмент.

19. Из концов дуги ABC, содержащей 120°, проведены касательные до взаимного пересечения в точке D, и в полученную фигуру ABCD вписана окружность. Доказать, что длина этой окружности равна длине дуги ABC.

20. На чертеже 29 даны вид и размеры в сантиметрах коленчатой трубы паровой машины. Найти её длину. (Её длина измеряется по средней пунктирной линии.)

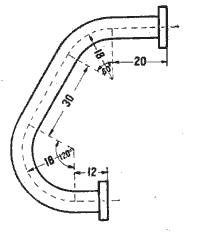
Черт. 29

21. Найти радиус такой окружности, длина и площадь круга которой выражаются одним и тем же числом.

22. Определить относительную погрешность при замена длины полуокружности 1 /₂ С через a₃ + a₄ (для приближённого спрямления окружности).

23. Одно из приближённых спрямлений окружности состоит в том, что её заменяют периметром прямоугольного треугольника, у которого один катет равен 6 /₅ диаметра, другой катет составляет 3 /₅ диаметра. Определить абсолютную погрешность.

24. Определить площадь круга при следующей длине радиуса:
1) 10 м; 2) 4 дм; 3) 2,6 см (взять π =3,14).

25. Определить радиус круга, если его площадь равна: 1) 2 см 2 ; 2) 50 м 2 ; 3) 17 дм 2 .

26. Лошадь привязана к колу верёвкой, длина которой равна 10,5 м. Найти площадь участка, на котором она может пастись. (С точностью до 0,01 кв. м.)

27. Найти площадь круга поршня воздушного насоса, диаметр которого равен 10 см.

28. Поршень насоса имеет площадь сечения в 12,56 см 2 . Найти диаметр поршня.

29. Дерево имеет 1,884 м в обхвате. Чему равна площадь его поперечного сечения, имеющего (приблизительно) форму круга?

30. Какой груз выдерживает пеньковый канат, имеющий 18 см в окружности, если допускаемая нагрузка равна 100 кгсм 2

31. 1) Определить площадь круга, если длина окружности равна 8 см.

1) Определить длину окружности, если площадь круга равна 18 см 2 .

32. 1) Пропускная способность трубы III (черт. 30) та же, что и у труб I и II вместе. Определить построением величину x по данным на чертеже размерам.

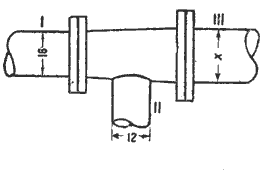
Черт. 30.

2) Две трубы с диаметром в 6 см и в 8 см требуется заменить одной трубой той же пропускной способности. Найти диаметр этой трубы.

33. Определить площадь круга, если площадь вписанного квадрата равна F.

34. Вычислить площадь круга, если она менее площади описанного квадрата на 4,3 м 2 .

35. Найти отношение между площадями вписанного и описанного кругов: 1) для правильного треугольника; 2) для квадрата; 3) для правильного шестиугольника.

36. Вертикальный цилиндрический котёл 78 см в диаметре и весящий 752 кг имеет в днище круглое отверстие, наружный диаметр которого равен 36 см. Всей площадью своего днища котёл опирается на фундамент. Определить давление, оказываемое котлом вследствие его тяжести на 1 см 2 поверхности фундамента.

37. В кольце, образованном двумя концентрическими окружностями, хорда большей окружности, касающаяся меньшей, равна а. Определить площадь кольца.

38. Круга касаются шесть равных ему кругов, касающихся также между собой, и полученное соединение семи равных кругов охвачено таким концентрическим кольцом, которое равновелико их сумме. Доказать, что ширина кольца равна радиусу кругов.

Сектор и сегмент.

39. Определить площадь сектора, если радиус равен r, а дуга содержит:
1) 67°30′; 2) 15°45′.

40. Определить радиус сектора, если его площадь равна q, а центральный угол равен: 1) 72°; 2) 36′.

41. Радиус сектора равен r, а площадь равна q. Определить величину центрального угла (или дуги).

42. Определить площадь сегмента, если радиус равен R, а дуга содержит: 1) 90°; 2) 60°; 3) 45°; 4) 30°.

43. Определить площадь сегмента, если хорда равна а, а дуга содержит: 1) 120°; 2) 90°; 3) 60°.

Площадь фигур, ограниченных прямыми и дугами окружностей.

44. Определить площадь окна (черт. 31), имеющего форму прямоугольника, законченного вверху дугой круга в 60°; высота окна, считая от середины дуги до основания, равна 2,4 м, ширина его 1,6 м.

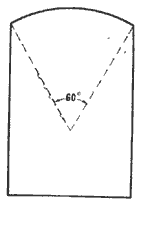
Черт. 31

45. 1) Полуокружность радиуса r разделена на три равные части, и точки деления соединены с концом диаметра. Определить площадь средней части полукруга.

2) Концы дуги CD одинаково удалены соответственно от концов диаметра АВ. Определить площадь, заключённую между дугой CD и хордами АС и AD, если площадь круга равна Q и дуга CD содержит п°.

46. В круге радиуса R проведены по одну сторону центра две параллельные хорды, из которых одна стягивает дугу в 120°, а другая в 60°. Определить часть площади круга, заключённую между хордами.

47. Общая хорда двух пересекающихся окружностей равна а и стягивает в одном круге дугу в 60°, а в другом— дугу в 90°. Определить площадь общей части кругов (два случая).

48. Площадь круга Q. Определить площадь вписанного в него прямоугольника, стороны которого относятся, как т : п.

49. В круг радиуса R вписан прямоугольник, площадь которого составляет половину площади круга. Определить стороны этого прямоугольника.

50. Около круга, площадь которого равна Q, описан ромб с углом в 30°. Определить площадь этого ромба.

51. Около правильного треугольника с площадью Q описана окружность, и в тот же треугольник вписана окружность. Определить площадь кольца, заключённого между этими окружностями.

52. АМВ—дуга, содержащая 120°; OA и ОВ—радиусы; АС и ВС—касательные; DME—дуга, описанная из центра С между СА и СВ и касающаяся дуги АМВ. Найти отношение между площадями секторов CDME и ОАМВ.

53. Из концов дуги АСВ проведены касательные до пересечения в точке D. Определить площадь DACB, заключённую между двумя касательными и дугой, если радиус равен R, а дуга содержит: 1) 90°; 2) 120°; 3) 60°.

54. Из центра равностороннего треугольника описана окружность, пересекающая его стороны так, что внешние дуги содержат по 90°. Обозначая сторону этого треугольника через а, определить площадь, ограниченную внутренними дугами и средними отрезками сторон.

55. 1) Во сколько раз увеличится площадь круга, если диаметр его увеличить в 3 раза? Во сколько раз площадь уменьшится, если радиус уменьшить в 5 раз?

2) Во сколько раз надо уменьшить радиус круга, чтобы площадь уменьшилась в 4 раза? Во сколько раз надо увеличить диаметр круга, чтобы площадь увеличилась в 5 раз?

56. Можно ли водопроводную трубу диаметром в 50 мм заменить двумя трубами диаметром в 25 мм каждая? Одинакова ли площадь сечения одной большой трубы и двух малых?

57. Вычислить площадь заштрихованной части прямоугольника, данного
на чертеже 32.

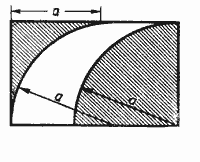
Черт. 32.

58. Определить площадь фигур, заштрихованных на чертежах 33 — 36, по данным размерам.

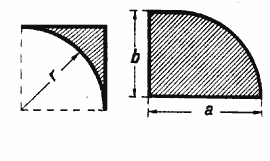
Черт. 33 Черт.34

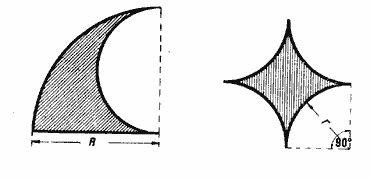
Черт.35 Черт.36

59. Два равных полукруга наложены так, что диаметры их параллельны, а полуокружность одного проходит через центр другого. Определить площадь общей части полукругов по данному их радиусу R.

60. На каждой стороне квадрата, принятой за диаметр, описана полуокружность, лежащая внутри квадрата. Определить площадь полученной розетки, если стороны квадрата равны а.

61. На сторонах ромба описаны, как на диаметрах, полуокружности, обращенные внутрь. Диагонали ромба равны а и b. Определить площадь полученной розетки.

62. Диаметр разделён на равные части, из обоих его концов проведены полуокружности во все точки деления, причём из одного конца все полуокружности сверху, а из другого все снизу. Доказать, что полученными изогнутыми линиями круг разделился на части равной величины, а периметр каждой части равен длине окружности.

63. В равностороннем треугольнике проведены дуги между каждыми двумя вершинами через центр треугольника (черт. 37). Сторона треугольника равна а. Определить площадь полученной розетки.

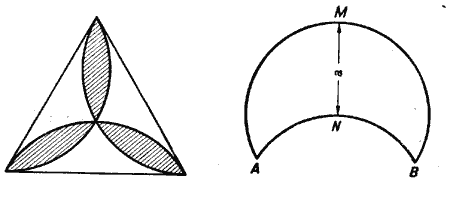
Черт. 37 Черт. 38

64. Между точками А и В проведены две дуги, обращенные выпуклостью в одну сторону: дуга АМВ содержит 240° и дуга ANB 120°. Расстояние между серединами этих, дуг равно а. Определить площадь луночки (черт. 38).

65. АВ и CD— два взаимно перпендикулярных диаметра. Из точки D, как из центра, радиусом DA описанa дуга АМВ. Доказать, что луночка АМВС равновелика треугольнику ABD.

66. Из точки С данной полуокружности опущен перпендикуляр CD на диаметр АВ, и на отрезках AD и DB построены новые полуокружности по одну сторону с данной. Доказать, что площадь, заключённая между тремя полуокружностями, pавна площади круга с диаметром CD.

67. Вычислить площадь фигуры, заштрихованной на чертеже 39. Размеры даны в миллиметрах.

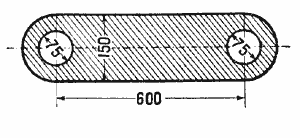
Черт. 39

68. Вычислить площадь сечения, изображённого на чертеже 40. Размеры даны в миллиметрах.

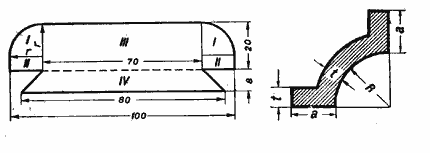
Черт. 40 Черт. 41

69. Определить площадь поперечного сечения фасонного железа, изображённого на чертеже 41.

70. Две параллельные хорды равны 15 м и 40 м, а расстояние между ними 39 м. Определить площадь круга.

71. Определить радиус круга, вписанного в данный сектор, если радиус сектора равен R, а дуга содержит α градусов [α равно: 1) 60°; 2) 90°; 3) 120°].

💡 Видео

7 класс. Геометрия. Взаимное расположение двух окружностей. 28.04.2020.Скачать

Определение центра дуги окружности, построение окружности по 3 точкамСкачать

ОГЭ № 25. "Окружности касаются внешним образом... "Скачать

6 класс. Математика. Урок 27. "Окружность и круг. Длина окружности. Площадь круга."Скачать

Применение определенного интеграла при решении геометр. и физических задач. Практ. часть. 11 класс.Скачать

Как найти центр окружности по трём точкамСкачать

Интерференция в тонких плёнках и кольца НьютонаСкачать

Деление окружности на 3; 6; 12 равных частейСкачать