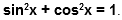Если посмотреть на числовую окружность , то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).

(() (frac) (;2π)) — четвертая четверть
- Почему так важно определять какой четверти принадлежит угол?
- Про непостоянство четвертей:
- Тригонометрия простыми словами
- Значения тригонометрических функций для первой четверти круга (0° – 90°)
- Принцип повтора знаков тригонометрических функций
- Тригонометрический круг
- Углы в радианах
- Единичная окружность
- Единичная окружность в тригонометрии
- 🎬 Видео
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Почему так важно определять какой четверти принадлежит угол?
Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций .
Например, для любого угла из второй четверти — синус положителен, а косинус , тангенс и котангенс отрицательны. А для любого угла из первой четверти — все четыре функции будут положительны.
Теперь давайте рассмотрим пример задачи, которую не решить без использования знаний про четверти.
Пример (ЕГЭ):
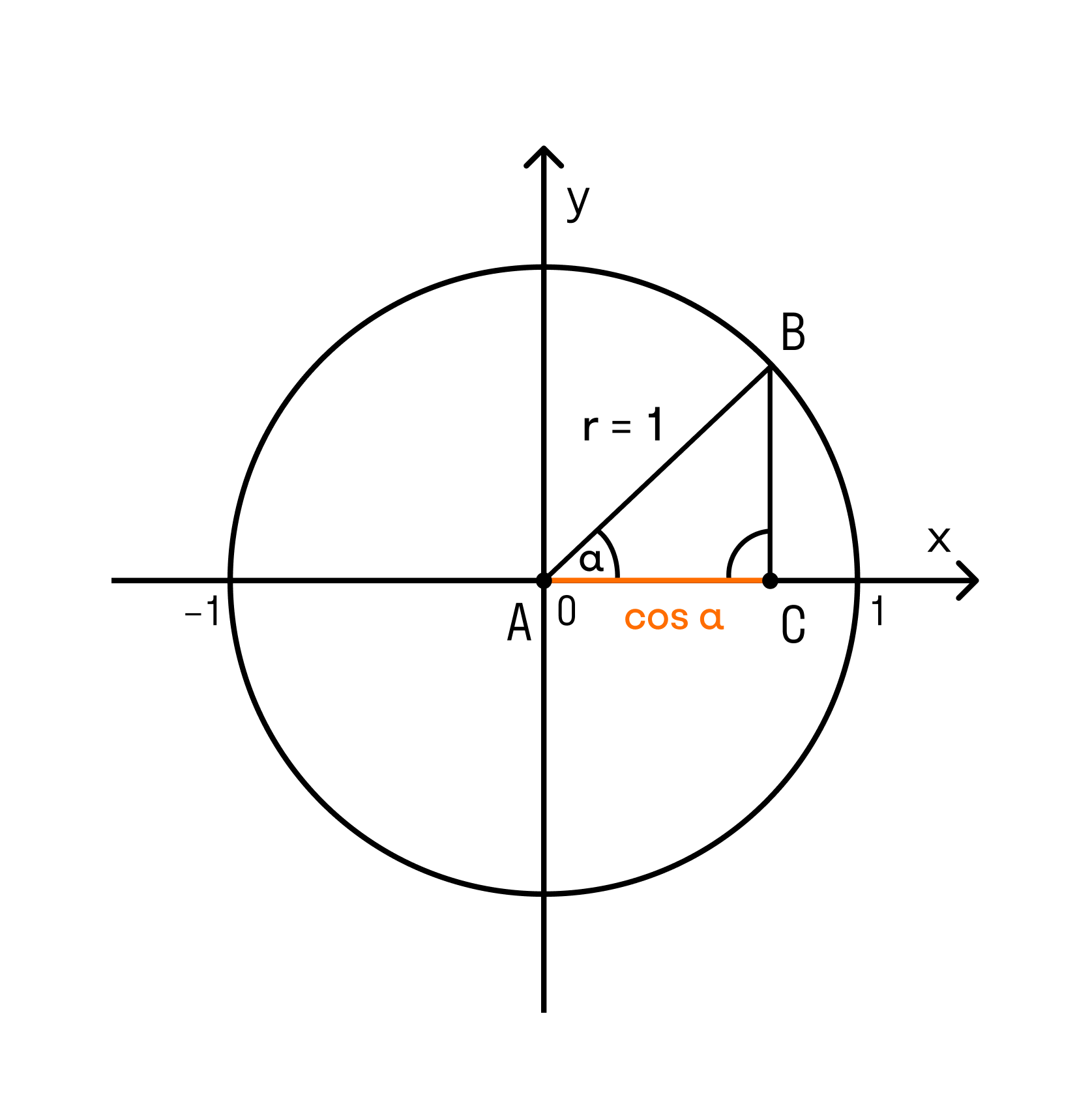
 ((0;-) (frac) ()) — четвертая четверть Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную. Видео:Тригонометрическая окружность. Как выучить?Скачать  Тригонометрия простыми словамиОфициальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах». Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике:
 Или в виде формул: Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1). Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла. Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB. Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°. Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный. Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов. Значения тригонометрических функций |
| 0° | 30° | 45° | 60° | 90° | sin | 0 | 1 | √3 | – | ctg | – | √3 | 1 | Принцип повтора знаков тригонометрических функцийУгол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону. В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ. Например, значения тригонометрических функций для углов 270° и -90° равны. Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно. Видео:В какой четверти находится точка единичной окружности, полученная при повороте Ро(1;0) на угол...Скачать  Тригонометрический кругУглы в радианахДля математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан. Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π . Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций. Видео:Как запомнить тригонометрический круг специально ничего не выучивая?Скачать  Единичная окружностьО чем эта статья: 10 класс, ЕГЭ/ОГЭ Статья находится на проверке у методистов Skysmart. Видео:🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать  Единичная окружность в тригонометрииВсе процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение. Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице. Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра. Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью. Поясним, как единичная окружность связана с тригонометрией. В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности. Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA. Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности. Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так: Радиан — одна из мер для определения величины угла. Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса. Число радиан для полной окружности — 360 градусов. Длина окружности равна 2πr, что превышает длину радиуса в 2π раза. Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан. Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса. Уравнение единичной окружности При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество: Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам. 🎬 Видео12 часов Тригонометрии с 0.Скачать  ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать  Найти знак тригонометрической функции (bezbotvy)Скачать  Вся Тригонометрия для Чайников, 10 класс, урок 1Скачать  Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать  Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать  ✓ Тригонометрия: с нуля и до ЕГЭ | #ТрушинLive #030 | Борис ТрушинСкачать  Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать  Период тригонометрических функций в радианах с числом Пи. В какой четверти находится угол поворота.Скачать  Ось симметрииСкачать  Знаки синуса, косинуса, тангенса ЛекцияСкачать 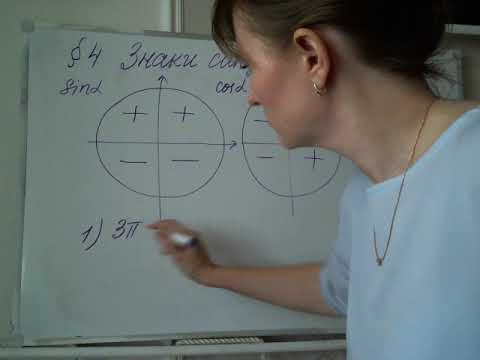 18+ Математика без Ху!ни. Формулы ПриведенияСкачать  Тригонометрическая окружность для непонимающихСкачать  Период тригонометрических функций тангенс и котангенс в градусах В какой четверти находится угол поСкачать  |
|---|