В каком случае прямая и окружность не имеют общих точек

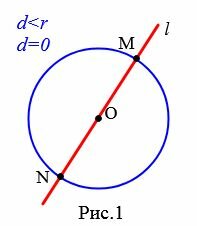
Выясним количество общих точек прямой и окружности в зависимости от их взаимного расположения. Если прямая l проходит через центр O окружности (Рис.1), то она пересекает окружность в двух точках, которые являются концами диаметра окружности.

Пусть прямая не проходит через центр окружности. Проведем перпендикуляр OH к прямой l (Рис.2, Рис.3, Рис.4). Обозначим расстояние от центра окружности до прямой l буквой d. Рассмотрим сколько общих точек будут иметь прямая и окружность в зависимости от соотношения d и r.

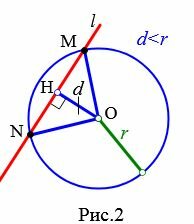Теорема 1. Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.

В этом случае прямая называется секущей по отношению к окружности.

Доказательство. Пусть расстояние от центра окружности до прямой меньше радиуса окружности: d Теорема 2. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.

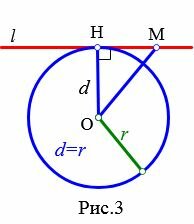Доказательство. Пусть расстояние от центра окружности до прямой равно радиусу окружности: d=r (Рис.3). В этом случае OH=r, т.е. точка H лежит на окружности и является общей точкой прямой l и окружности. Возьмем на прямой l любую точку M отличной от H. Тогда расстояние от OM больше расстояния OH=r, поскольку наклонная OM больше перпендикуляра OH к прямой l. Следовательно точка M не лежит на окружности. Получили, что точка H единственная общая точка прямой l и окружности.

Теорема 3. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.

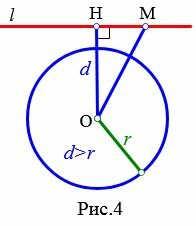Доказательство. Пусть расстояние от центра окружности до прямой больше радиуса окружности:d>r (Рис.4). Тогда ( small OH > r). Возьмем на прямой l любую точку M отличной от H. Тогда ( small OM > OH>r). Следовательно точка M не лежит на окружности. Таким образом, если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.

Видео:Взаимное расположение окружностей. Окружности не имеют общих точек.Скачать

Окружность. Относительное взаимоположение окружностей.

Если две окружности имеют только одну общую точку, то говорят, что они касаются.

Если же две окружности имеют две общие точки, то говорят, что они пересекаются.

Трех общих точек две не сливающиеся окружности иметь не могут, потому, что в противном случае через три точки можно было бы провести две различные окружности, что невозможно.

Будем называть линией центров прямую, проходящую через центры двух окружностей (например, прямую OO₁).

Теорема.

Если две окружности имеют общую точку по одну сторону от линии центров, то они имеют общую точку и по другую сторону от этой линии, т.е. такие окружности пересекаются.

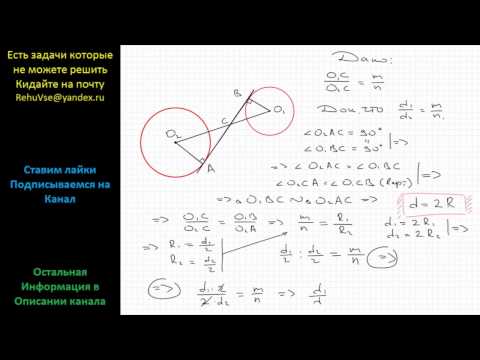
Пусть окружности O и O₁ имеют общую точку A, лежащую вне линии центров OO_1. Требуется доказать, что эти окружности имеют еще общую точку по другую сторону от прямой OO₁.

Опустим из A на прямую OO₁ перпендикуляр AB и продолжим его на расстояние BA₁, равное AB. Докажем теперь, что точка A₁ принадлежит обеим окружностям. Из построения видно, что точки O и O₁ лежат на перпендикуляре, проведенном к отрезку AA₁ через его середину. Из этого следует, что точка O одинаково удалена от A и A₁. То же можно сказать и о точке O₁. Значит обе окружности, при продолжении их, пройдут через A₁.Таким образом, окружности имеют две общие точки : A (по условию) и A₁ (по доказанному). Следовательно, они пересекаются.

Следствие.

Общая хорда (AA₁) двух пересекающихся окружностей перпендикулярна к линии центров и делится ею пополам.

Теоремы.

1. Если две окружности имеют общую точку на линии их центров или на ее продолжении, то они касаются.

2. Обратно: если две окружности касаются, то общая их точка лежит на линии центров или на ее продолжении.

Признаки различных случаев относительного положения окружностей.

Пусть имеем две окружности с центрами O и O₁, радиусами R и R₁ и расстоянием между центрами d.

Эти окружности могут находиться в следующих 5-ти относительных положениях:

1. Окружности лежат одна вне другой, не касаясь. В этом случае, очевидно, d > R + R₁ .

2. Окружности имеют внешнее касание. Тогда d = R + R₁, так как точка касания лежит на линии центров O O₁.

3. Окружности пересекаются. Тогда d R + R₁, потому что в треугольнике OAO₁ сторона OO₁ меньше суммы, но больше разности двух других сторон.

4. Окружности имеют внутреннее касание. В этом случае в d = R — R₁, потому что точка касания лежит на продолжении линии OO₁.

5. Одна окружность лежит внутри другой, не касаясь. Тогда, очевидно,

d R + R₁, то окружности расположены одна вне другой, не касаясь.

2. Если d = R + R₁, то окружности касаются извне.

3. Если d R — R₁, то окружности пересекаются.

4. Если d = R — R₁, то окружности касаются изнутри.

5. Если d R Е R₁. Значит, все эти случаи исключаются. Остается один возможный, именно тот, который требовалось доказать. Таким образом, перечисленные признаки различных случаев относительно положения двух окружностей не только необходимы, но и достаточны.

Видео:№35. Через точку М, не лежащую на прямой а, проведены две прямые, не имеющие общих точек с прямой а.Скачать

Сколько общих точек имеет прямая и окружность если

Видео:Окружность и прямая: варианты взаимного расположенияСкачать

Взаимное расположение прямой и окружности

Выясним количество общих точек прямой и окружности в зависимости от их взаимного расположения. Если прямая l проходит через центр O окружности (Рис.1), то она пересекает окружность в двух точках, которые являются концами диаметра окружности.

Пусть прямая не проходит через центр окружности. Проведем перпендикуляр OH к прямой l (Рис.2, Рис.3, Рис.4). Обозначим расстояние от центра окружности до прямой l буквой d. Рассмотрим сколько общих точек будут иметь прямая и окружность в зависимости от соотношения d и r.

Теорема 1. Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.

В этом случае прямая называется секущей по отношению к окружности.

Доказательство. Пусть расстояние от центра окружности до прямой меньше радиуса окружности: d Теорема 2. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.

Доказательство. Пусть расстояние от центра окружности до прямой равно радиусу окружности: d=r (Рис.3). В этом случае OH=r, т.е. точка H лежит на окружности и является общей точкой прямой l и окружности. Возьмем на прямой l любую точку M отличной от H. Тогда расстояние от OM больше расстояния OH=r, поскольку наклонная OM больше перпендикуляра OH к прямой l. Следовательно точка M не лежит на окружности. Получили, что точка H единственная общая точка прямой l и окружности.

Теорема 3. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.

Доказательство. Пусть расстояние от центра окружности до прямой больше радиуса окружности:d>r (Рис.4). Тогда ( small OH > r). Возьмем на прямой l любую точку M отличной от H. Тогда ( small OM > OH>r). Следовательно точка M не лежит на окружности. Таким образом, если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.

Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Сколько общих точек могут иметь прямая и окружность? Рассмотри все возможные случаи и сделай рисунки. Является ли это разбиение классификацией?

Видео:Геометрия Окружности с центрами в точках O1 и O2 не имеют общих точек. Внутренняя общая касательнаяСкачать

Ваш ответ

Видео:8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать

решение вопроса

Видео:Геометрическое место точек окружность и круг - 7 класс геометрияСкачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 606,989
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Прямая и окружность. Математика. 6 класс.Скачать

Сколько общих точек имеет прямая и окружность, если радиус окружности 4 см, а расстояние от ее центра до прямой равно : а) 3 см ; б) 4 см ; в) 5 см?

Геометрия | 5 — 9 классы

Сколько общих точек имеет прямая и окружность, если радиус окружности 4 см, а расстояние от ее центра до прямой равно : а) 3 см ; б) 4 см ; в) 5 см?

в) не имеет точек.

Видео:70. Взаимное расположение прямой и окружностиСкачать

Расстояние от центра окружности до прямой равно 7 см, диаметр окружности равен 16 см?

Расстояние от центра окружности до прямой равно 7 см, диаметр окружности равен 16 см.

Определите, сколько общих точек имеют окружность и прямая.

1) одну 2) две 3) ни одной 4) множество.

Видео:9 класс, 8 урок, Взаимное расположение двух окружностейСкачать

Радиусы двух окружностей равны 6 см и 10 см, а расстояние между их центрами равно 9 см?

Радиусы двух окружностей равны 6 см и 10 см, а расстояние между их центрами равно 9 см.

Определить сколько общих точек имеют эти окружности.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Расстояние от центра окружности до прямой равно 7 см, диаметр окружности равен 16 см?

Расстояние от центра окружности до прямой равно 7 см, диаметр окружности равен 16 см.

Определите, сколько общих точек имеют окружность и прямая.

Видео:Взаимное расположение двух окружностей. Урок 8. Геометрия 9 классСкачать

Решите плиззз задачу))) Проведите прямые через каждые две точки?

Решите плиззз задачу))) Проведите прямые через каждые две точки.

Сколько общих точек имеет каждая из прямых с окружностью?

Ответ : (Вставить) Прямая _____ и окружность не имеют общих точек.

Прямая _____ и окружность имеют тольку одну _________________ точку.

Прямая______, _______, _______, _______ и окружность имеют две общин точки.

Видео:Взаимное расположение окружности и прямой. 7 класс.Скачать

Какие из следующих утверждений верны?

Какие из следующих утверждений верны?

1) Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.

2) Если радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 3, то эти окружности не имеют общих точек.

3) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются.

4) Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.

Видео:Теорема о числе точек пересечения двух окружностейСкачать

Может ли раастояние от центра окружности до прямой равняться радиусу окружности?

Может ли раастояние от центра окружности до прямой равняться радиусу окружности?

Видео:ОГЭ за одну минуту | ОГЭ, математика, задание 16 (окружность и касательная)Скачать

Растояние от центра окружности до прямой равно 9см?

Растояние от центра окружности до прямой равно 9см.

При каком значении радиуса окр r прямая имеет с окружностью две общие точки?

Растояние от центра окружности до прямой равно 11см.

При каком значении радиуса окр r прямая не имеет с окр общих точек?

Видео:71. Касательная к окружностиСкачать

Какие из следующих утверждений верны?

Какие из следующих утверждений верны?

1. Если радиус окружности равен 7, а расстояние от центра окружности до прямой равно 5, то эти прямая и окружность не имеют общих точек.

2. Сумма двух противоположных углов четырёхугольника равна 180.

3. Центр окружности, описанной около прямоугольного треугольника, лежит на стороне этого треугольника.

Видео:Касательная и секущая к окружности encodedСкачать

Радиусы двух окружностей равны 6см и 9см, а расстояние между их центрами равно 9 см?

Радиусы двух окружностей равны 6см и 9см, а расстояние между их центрами равно 9 см.

Определите, сколько общих точек имеют эти окружности.

Видео:Геометрия. 7 класс. Взаимное расположение прямой и окружности /13.04.2021/Скачать

Даны две прямые общей точкой О , окружности с радиусами 3 и 4 касаются обеих прямых?

Даны две прямые общей точкой О , окружности с радиусами 3 и 4 касаются обеих прямых.

Чему может быть равно расстояние между центрами ?

( все возможные варианты).

Перед вами страница с вопросом Сколько общих точек имеет прямая и окружность, если радиус окружности 4 см, а расстояние от ее центра до прямой равно : а) 3 см ; б) 4 см ; в) 5 см?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

Задание № 7 : На стороне AB равностороннего треугольника ABC взята точка D так, что сумма расстояний от нее до сторон AC и BC равна 16 см. Найдите высоту треугольника, проведенную из вершины C. РЕШЕНИЕ : Пусть сторона треугольника а. Одно из данны..

MN – PQ – NM + PT + PQ + TR — NM = MN⇒MN — NM = 2MN — PQ + PQ = 0 PT + TR = PR 2MN + PR.

А) Пусть х — коэффициент пропорциональности. Тогда углы четырехугольника : 2х, 4х, 5х, 7х Сумма углов выпуклого четырехугольника равна 360°. Составляем уравнение : 2x + 4x + 5x + 7x = 360° 18x = 360° x = 20° Наибольший угол : 7 · 20° = 140° Наимень..

Угол A = углу C = 360 — (40 * 2) : 4 = 70° Угол B = углу D = 70 + 40 = 110°.

Пусть A это х то В это х + 40 так как А + В = 90, то х + х + 40 = 90 х + х = 50 х = 25 А = 25 В = А + 40 В = 25 + 40 = 65 А = С = 25 В = D = 65.

Симметрия — это соответствие, неизменность, которая проявляется при каких — либо изменениях.

РЕШЕНИЕ Формула боковой поверхности конуса S = π * R * L, где L — образующая конуса. — гипотенуза прямоугольного треугольника. Образующая — L — катет при угле 45° L = √2 * R = 5√2 И находим площадь S = π * 5 * 5 * √2 = 25√2 * π — ОТВЕТ Рисунок — в ..

Надеюсь что понятно.

R = a / корень из 2 — формула нахождения радиуса описанной окружности. А — сторона квадрата R = 8 * корень из 2 / корень из 2 = 8 (сокращаем корни).

А)Около четырехугольника можно описать окружность, если суммы углов равны 180°. По теореме косинусов из треугольника АВС : АC2 = AB2 + CB2–2·AB·CB·cos∠B 49 = 9 + 25–30·cos∠B cos∠B = 15 / (–30) = –1 / 2 По теореме косинусов из треугольника АDС : АC2 ..

🎦 Видео

Взаимное расположение прямой и окружности | Геометрия 7-9 класс #68 | ИнфоурокСкачать

При каких значениях m прямая y = m не имеет с графиком ни одной общей точки.Скачать