Сначала построим квадрат D1E1F1G1 так, чтобы вершины F1 и G1 лежали на стороне АС, а вершина D1 — на стороне АВ.
Гомотетия относительно вершины А, переводящая точку Е1, в точку Е, лежащую на стороне ВС, переводит D1 в D, F1 в F, Gi в G.
Так как гомотетия переводит фигуру в подобную фигуру, то четырехугольник DEFG — искомый квадрат.

задача №9
к главе «§11. Подобие фигур».
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Модуль 1. Метод подобия
Модуль 1. Метод подобия
Метод подобия при решении задач на построение.
В задачах на построение данные бывают двух видов: одни определяют вид фигуры, которую нужно построить, другие – её размеры. В этом случае удобно использовать метод подобия. Построение проводится поэтапно: сначала строят фигуру, подобную искомой, потом строят по заданным размерам саму искомую фигуру.
Рассмотрим применение метода на следующей задаче.
Задача 2. В данный треугольник вписать квадрат так, чтобы две его вершины лежали на основании треугольника, а две других – на его боковых сторонах.
Решение. Пусть дан треугольник АВС. Нужно вписать в него квадрат.
Анализ. Предположим, что задача решена и искомый квадрат построен. Он подобен любому квадрату, у которого две вершины лежат на стороне АС, а третья – на стороне АВ.

1. Строим произвольный квадрат Н1М1К1Т1, у которого две вершины лежат на стороне АС, а третья – на стороне АВ (пока не обращаем внимания на требование к четвёртой вершине).
· Из произвольной точки М1 опускаем перпендикуляр на АС, получаем точку Н1 , отрезок М1Н1 – сторона квадрата.
· На АС от точки Н1 отложим отрезок Н1Т1, равный М1Н1, получим вторую сторону квадрата.
· Из точек М1 и Т1 проведем окружности радиусом М1Н1. На пересечении получим точку К1.
· Соединим точки, получим Н1М1К1Т1 – квадрат, у которого одна вершина не лежит на стороне треугольника.
2. Проведем луч АК1 до пересечения со стороной ВС, получим точку К.
3. Из точки К проведем прямую параллельно АС до пересечения с АВ, получим точку М.
4. Из точки К проведем прямую параллельно М1Н1 до пересечения с АС, получим точку Т; из точки М проведем прямую параллельно М1Н1 до пересечения с АС, получим точку Н.
5. Получили квадрат МКТН. Докажем, что квадрат МКТН – искомый.
КМ÷÷ АС; НТ ÷÷ АС; отсюда, КМ÷÷ НТ. Значит, МКТН – параллелограмм.
М1 Н1 


D AКМ с тем же коэффициентом k; так как АК = k ∙ АК1 . Значит, МК = k ∙ М1К1 .
М1К1 = Т1К1 как стороны квадрата, отсюда МК = КТ. Следовательно, прямоугольник МКТН — квадрат, вершины которого лежат на сторонах АС и АВ.
Задача 3. Построить квадрат, равновеликий данному равностороннему треугольнику.
Решение. Пусть дан треугольник АВС – равносторонний со стороной а. Нужно построить такой квадрат, у которого площадь будет равной площади данного треугольника.
Анализ. Предположим, что задача решена и искомый квадрат со стороной х построен.
Тогда площадь треугольника S =
Получим равенство x2 = 

части равенства произведение длин высоты и половины стороны равностороннего
треугольника, т. е. х – среднее пропорциональное этих отрезков. Мы свели задачу к известной.
Построение. В данном треугольнике построим высоту. В результате построения получим отрезки длиной 







На полученном отрезке АВ, как на диаметре, строим окружность. Из точки Н восстановим перпендикуляр до пересечения с окружностью, получим точку М: отрезок НМ — среднее пропорциональное между отрезками АН и НВ диаметра. Построим квадрат со стороной МН. Квадрат МКРН – искомый.
Задача 4. Построить круг, площадь которого в три раза больше площади данного круга. Решение. Пусть дан круг радиуса R. Нужно построить такой круг, у которого площадь будет равна утроенной площади данного круга.

Тогда площадь данного круга S=πR2, площадь искомого круга πx2.
Преобразуем равенство πx2 = 3πR2 и получим x = R




Построение. В данном круге с центром О построим два перпендикулярных диаметра. Из конца диаметра А проведём дугу радиуса 2R до пересечения с продолжением другого диаметра. Получим точку М. Длина отрезка ОМ равна R
Радиусом равным ОМ построим окружность.
В результате построения получим искомый круг.
Решение задач с использованием метода подобия.
Задача 5. Биссектриса угла при основании равнобедренного треугольника отсекает от данного треугольника подобный ему треугольник. Найти углы данного треугольника.


Учителю: надо, чтобы ученики обязательно — алгебраически или геометрически — убедились, что в верхнем треугольнике не может быть таких же углов, как в данном, значит, только DСАМ
DСАМ, то треугольник DСАМ тоже равнобедренный. Значит ÐАМС = ÐС.
2. ÐМАС = 

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Как в треугольник вписать квадрат?(с поддержкою циркуля и линейки)
Как в треугольник вписать квадрат?(с поддержкою циркуля и линейки)
- Ева Покладкина
- Математика 2019-07-17 18:14:09 0 1
1)выделим основание треугольника, на котором будет находиться одна из сторон
допустим это основание горизонтальное АС и верхушка В
2)выберем из боковых сторон AB и CB сторону, образующую с острый угол с основанием — к примеру АВ
3) на стороне АВ выберем произвольную точку M
4) опустим перпендикуляр на АС из точки М в точку К
5) построим квадрат, дотрагивающийся АВ в точке М, со стороной одинаковой МК
6) интересует та вершина квадрата, не лежащая на нижнем основании и не M
назовем ее E
7) проведем прямую АЕ
8) если АСB — тупой, то АЕ до скрещения с перпендикуляром к АC, проходящим через точку C
9) если АСВ — не тупой, то АЕ до скрещения с ВС
10) приобретенная точка Т
11) от Т опускаем перпендикуляр на АС и строим прямую параллельно АС до скрещения с АВ
мы получили 3 точки искомого квадрата, дальше дело техники
📺 Видео
Задача.Окружность и прямоугольник вписаны в квадрат.Скачать

Как построить квадрат, два способаСкачать
Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Строим вписанную в данный треугольник окружность (Задача 2).Скачать

8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

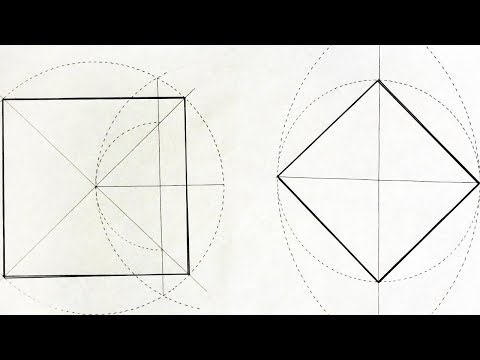
Как вписать квадрат в окружностьСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Задача.Окружность и прямоугольник вписаны в квадрат.Скачать

Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать

Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Построение квадрата циркулем по заданной сторонеСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

8 класс, 8 урок, Ромб и квадратСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Построение правильного квадрата.Скачать



