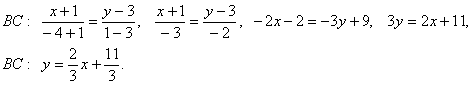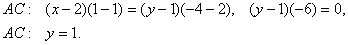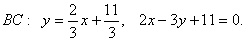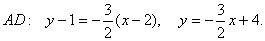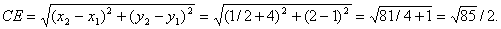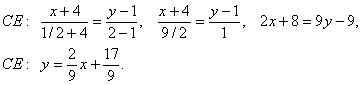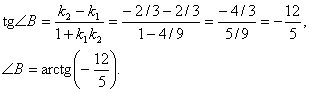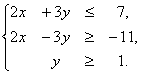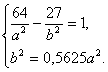Условие
1. Дан треугольник АВС, в котором А(6;2), В (2;-3), С (-3;5). Составить уравнение медианы, проведённой из вершины А.
2. Дан эллипс x^2/49 + y^2/24 = 1. Найти эксцентриситет эллипса и его фокусы.
3. Составить уравнение прямой, проходящей через фокус параболы у^2 = 4х перпендикулярно к прямой х-3у+1=0
Решение
Уравнение AМ, как уравнение прямой проходящей через две точки:
[m]frac<x_-x_>=frac<y_-y_>[/m]
Умножаем обе части на (-13):
[b]2х-13у+14=0[/b] — уравнение медианы AМ
2.
Каноническое уравнение эллипса
[m]frac+frac=1[/m]
Эксцентриситет
ε =с/а=5/7
3.
Каноническое уравнение параболы:
y^2=2px
F(p/2;0)
y^2=4x ⇒ 2p=4 ⇒ [b]p=2[/b]
Произведение угловых коэффициентов взаимно перпендикулярных прямых
k_(1)*k_(2)=-1
x-3y+1=0 запишем в виде y=[m]fracx+frac[/m]
Общий вид прямых перпендикулярных прямой x-3y+1=0
Прямая проходит через фокус параболы, т.е через точку F(1;0)
Видео:Уравнение параллельной прямойСкачать

Уравнение прямой проходящей через вершину параболы параллельно прямой
уравнение и длину высоты А D ; уравнение и длину медианы СЕ; внутренний угол В; систему линейных неравенств, определяющую треугольник. Сделать чертеж.
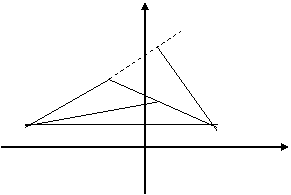
1. Составим уравнения всех сторон треугольника, используя уравнение прямой, проходящей через две данные точки.
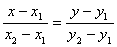
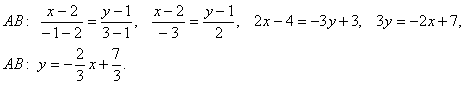
Так как точки А и С имеют одинаковую ординату, используем данное уравнение в преобразованном виде:
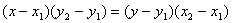
2. Найдем длину высоты А D . Используем формулу расстояния от точки до прямой:
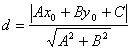
Приведем уравнение ВС к общему уравнению прямой.
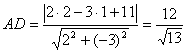
3. Составим уравнение высоты А D . Она проходит через точку А(2,1) и перпендикулярна прямой ВС, k BC =2/3. Из условия перпендикулярности k AD =-1/ k BC =-3/2. Воспользуемся уравнением прямой, проходящей через данную точку в данном направлении:
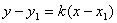
4. Для нахождения длины и уравнения медианы СЕ найдем координаты точки Е как середины отрезка АВ.
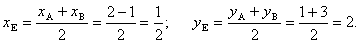
5. Найдем внутренний угол В. Он отсчитывается в положительном направлении от прямой ВС к прямой АВ. k BC =2/3, k AB =-2/3.
6. Составим систему линейных неравенств, определяющую треугольник. Запишем уравнения сторон в виде
AB : 2 x + 3 y = 7 ,
BC : 2 x — 3 y =- 11 ,
Подставим точку с координатами (-1, 2), лежащую внутри треугольника, в левые части равенств.
2 x — 3 y =- 2-6=-8>-11,
Следовательно, система неравенств, описывающая треугольник, имеет вид
Задача 2. Составить каноническое уравнение гиперболы, если известно, что ее эксцентриситет равен 1,25 и гипербола проходит через точку 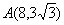
Решение . Каноническое уравнение гиперболы имеет вид 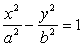
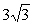
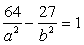
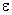
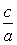
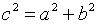
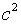
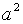
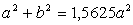
Итак, получаем систему двух уравнений с двумя неизвестными а и b .
Решая эту систему, находим 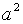
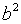
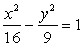
Задача 3. Составить уравнение прямой, проходящей через вершину параболы 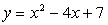
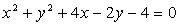
Решение . Найдем координаты вершины параболы и координаты центра окружности. Для этого выделим полные квадраты по каждой переменной.
Уравнение параболы: 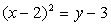
уравнение окружности: 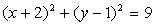
Следовательно, вершина параболы имеет координаты В (2;3), а центр окружности имеет координаты С (-2; 1).
Тогда уравнение искомой прямой составим по формуле
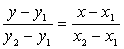
Получим 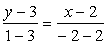
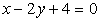
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Кривые второго порядка на плоскости
Уравнение вида Ах 2 +2Вху+Су 2 +2Dх+2Еу+F=0 называется общим уравнением кривой второго порядка. Коэффициенты уравнения – действительные числа, причем хотя бы одно из чисел А,В,С отлично от нуля. Такое уравнение определяет на плоскости окружность, эллипс, гиперболу или параболу.
В табл. 2 приведены уравнения кривых второго порядка и определен смысл входящих в них коэффициентов.
| № п/п | Определение кривой | Вид уравнения | Примечание | |||||
 Эллипс – множество всех точек плоскости, сумма расстояний от которых до двух точек, называемых фокусами, есть величина постоянная (рис.4) Эллипс – множество всех точек плоскости, сумма расстояний от которых до двух точек, называемых фокусами, есть величина постоянная (рис.4) |  — каноническое уравнение эллипса — каноническое уравнение эллипса | 2а – большая ось; 2b – малая ось 2с–межфокус-ное расстояние с 2 =а 2 -b 2 ; 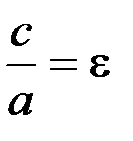 — эксцентриси-тет, 0 2 =а 2 +b 2 ; — эксцентриси-тет, 0 2 =а 2 +b 2 ; 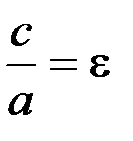 — эксцентри-ситет, e>1. Точки А1,А2 – вершины гиперболы. Прямые — эксцентри-ситет, e>1. Точки А1,А2 – вершины гиперболы. Прямые 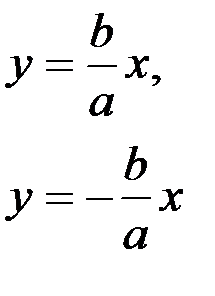 — асимптоты — асимптоты | ||||||
| 3. | Парабола — множество точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директриссой.
| у 2 =2px – каноническое уравнение параболы, симметричной относительно оси ОХ x 2 =2pу – каноническое уравнение параболы, симметричной относительно оси ОY (рис.6б) | F  — фокус, — фокус, 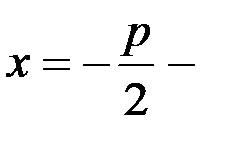 ди-ректриса. Точка (0;0) – вершина параболы (рис.6а) F ди-ректриса. Точка (0;0) – вершина параболы (рис.6а) F  — фокус, — фокус,  ди-ректриса. Точка (0;0) – вершина параболы (рис.6б) ди-ректриса. Точка (0;0) – вершина параболы (рис.6б) |
1. Найти координаты фокусов и эксцентриситет эллипса 36х 2 +100у 2 =3600.
Приведем уравнение эллипса к каноническому виду:
36х 2 +100у 2 =3600, поделим обе части уравнения на 3600:

С= 
Эксцентриситет: 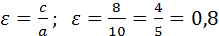
Ответ: Fл(-8,0); Fп(8,0); 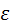
2.Написать уравнение прямой, проходящей через левую вершину эллипса 16х 2 +25у 2 =400 и точку М0(1;-3) (рис.7).
| у |
Решение:
| -4 |
| -5 |
| М |
| х |
| М0 |
| Рис. 7 |
Приведем уравнение 16х 2 +25у 2 =400 к каноническому виду.
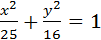
Левая вершина эллипса (-а,0)Þ(-5,0). Обозначим М(-5,0). Составим уравнение прямой, проходящей через точки М0 и М:
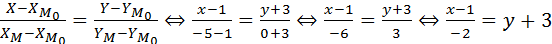
Ответ: 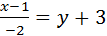
3. Написать уравнение прямой, проходящей через правый фокус гиперболы 9х 2 -16у 2 =144 и параллельно прямой 3х-2у+6=0 (рис.8).
| -3 |
| -4 |
| FП |
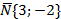 |
| х |
| у |
| Рис.8 |
Приведем уравнение 9х 2 -16у 2 =144 к каноническому виду 
Правый фокус гиперболы Fп(с,0);
С= 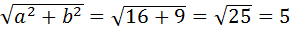
Пусть уравнение искомой прямой имеет вид y=k2x+b2;
Значит, y=(3/2)x+b2 проходит через точку Fп(5,0), то 0=(3/2)5+b2Þb2=-15/2. Итак, 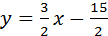
Искомая прямая проходит через точку Fл(5,0) параллельно прямой 3х-2у+6=0. Из общего уравнения заданной прямой определяем вектор нормали 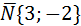
4. Написать уравнение прямой l, проходящей через нижнюю вершину эллипса 4х 2 +20у 2 =80, перпендикулярно прямой 2х—у+1=0 (рис.9).
| М |
 |
| -2 |
| y |
 |
| l |
| х |
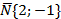 |
| Рис. 9 |
Приведем уравнение к каноническому виду 4х 2 +20у 2 =80,
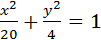
Нижняя вершина имеет вид: М(0;-b)=М(0;-2).
Условие перпендикулярности двух прямых: k1k3=-1.
k2=-1: k1Þk2=-1/2,
Так как прямая 

Итак, 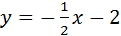
По условию задачи требуется написать уравнение прямой l, проходящей через точку М(0;-2) перпендикулярно прямой 2х—у+1=0. Из общего уравнения прямой определяем координаты вектора нормали 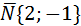
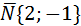
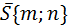

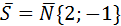

5. Написать уравнение прямой, проходящей через правый фокус эллипса 
Правый фокус эллипса имеет вид Fп(с,0);
С= 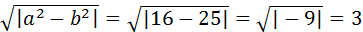
Так как прямая проходит под углом 45˚ к оси Ох, то k=tgα=tg45˚=1.
Пусть уравнение искомой прямой имеет вид: y=kx+b;
Так как прямая проходит через точку Fп(3,0), то 0=3+bÞb=-3.
Плоскость в пространстве
Любое уравнение первой степени в трехмерном пространстве определяет какую-либо плоскость.
Разным способам задания плоскости соответствуют различные виды уравнений (табл. 3.)
| № п/п | Вид уравнения | Смысл входящих в уравнение коэффициентов | Примечание |
| Уравнение плоскости, проходящей через данную точку перпендикулярно заданному вектору А(х-х0)+В(у-у0)+С(z-z0)=0 | (x0,y0,z0) – координаты заданной точки; АВС – координаты заданного вектора | Вектор N(А,В,С) называется нормальным вектором плоскости | |
| Общее уравнение плоскости Ах+Ву+Сz+D=0 | D=-Ax0-By0-Cz0, АВС – нормальный вектор плоскости; | Это уравнение получается из уравнения (1) эле-ментарными | |
| № п/п | Вид уравнения | Смысл входящих в уравнение коэффициентов | Примечание |
| х0,y0,z0 – координаты данной точки | преобразованиями | ||
Уравнение плоскости, проходящей через три заданные точки 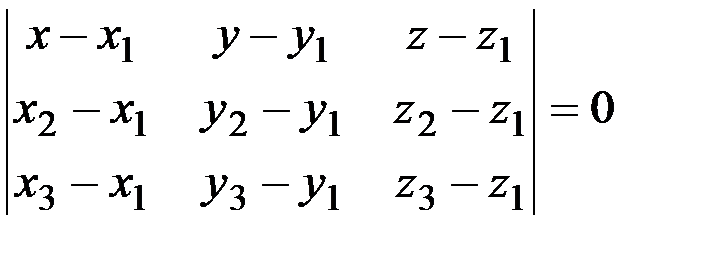 | М1(х1,y1,z1), М2(х2,y2,z2), М3(х3,y3,z3) – три точки, заданные своими координатами | Точки М1, М2, М3 не должны лежать на одной прямой | |
Уравнение плоскости в отрезках на осях 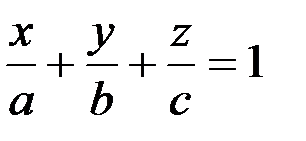 | а,b,c – отрезки, отсекаемые плоскостью от осей координат | аbc≠0 |
Пусть даны две плоскости a1 и a2:
Угол между двумя плоскостями определяется как 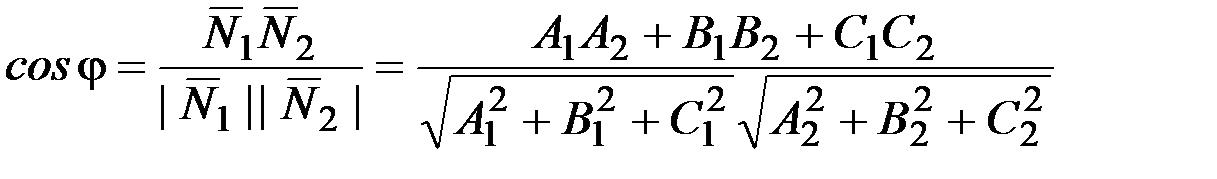
Условие перпендикулярности двух плоскостей:
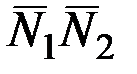
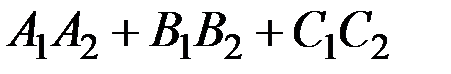
Условие параллельности двух плоскостей:


Расстояние от точки до плоскости:
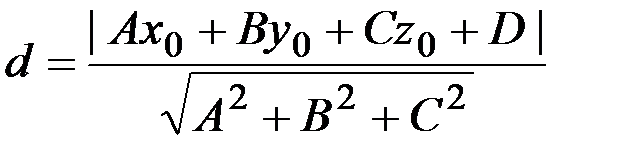
📺 Видео
9 класс, 7 урок, Уравнение прямойСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Видеоурок "Канонические уравнения прямой"Скачать

Уравнение прямой на плоскости. Решение задачСкачать

Написать канонические и параметрические уравнения прямой в пространствеСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

ВСЁ ПРО ГРАФИКИ ЕГЭ 2024 (Прямая, Парабола, Окружность, Модуль, Гипербола, Корень, Области, Сдвиги)Скачать

Лекция 23. Виды уравнений прямой на плоскости.Скачать

Видеоурок "Уравнение прямой, проходящей через две точки"Скачать

Составляем уравнение прямой по точкамСкачать

УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать

Видеоурок "Общее уравнение прямой"Скачать

Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

11. Прямая в пространстве и ее уравненияСкачать

213. Фокус и директриса параболы.Скачать