Даны две окружности. Требуется найти все их общие касательные, т.е. все такие прямые, которые касаются обеих окружностей одновременно.
Описанный алгоритм будет работать также в случае, когда одна (или обе) окружности вырождаются в точки. Таким образом, этот алгоритм можно использовать также для нахождения касательных к окружности, проходящих через заданную точку.
- Количество общих касательных
- Алгоритм
- Реализация
- Две окружности на плоскости. Общие касательные к двум окружностям
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- Касательная к окружности
- Касательная к окружности, секущая и хорда — в чем разница
- Свойства касательной к окружности
- Задача
- Задача 1
- Задача 2
- Задача 1
- Задача 2
- Задача 1
- Задача 2
- 🎬 Видео
Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Количество общих касательных
Сразу отметим, что мы не рассматриваем вырожденные случаи: когда окружности совпадают (в этом случае у них бесконечно много общих касательных), или одна окружность лежит внутри другой (в этом случае у них нет общих касательных, или, если окружности касаются, есть одна общая касательная).
В большинстве случаев, две окружности имеют четыре общих касательных.
Если окружности касаются, то у них будет три обших касательных, но это можно понимать как вырожденный случай: так, как будто две касательные совпали.
Более того, описанный ниже алгоритм будет работать и в случае, когда одна или обе окружности имеют нулевой радиус: в этом случае будет, соответственно, две или одна общая касательная.
Подводя итог, мы, за исключением описанных в начале случаев, всегда будем искать четыре касательные. В вырожденных случаях некоторые из них будут совпадать, однако тем не менее эти случаи также будут вписываться в общую картину.
Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Алгоритм
В целях простоты алгоритма, будем считать, не теряя общности, что центр первой окружности имеет координаты 
Обозначим через 

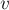
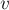
Для решения задачи подойдём к ней чисто алгебраически. Нам требуется найти все прямые вида 


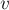
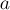
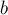


Чтобы избавиться от модулей, заметим, что всего есть четыре способа раскрыть модули в этой системе. Все эти способы можно рассмотреть общим случаем, если понимать раскрытие модуля как то, что коэффициент в правой части, возможно, умножается на 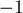
Иными словами, мы переходим к такой системе:
Введя обозначения 

Решение этой системы сводится к решению квадратного уравнения. Мы опустим все громоздкие выкладки, и сразу приведём готовый ответ:
Итого у нас получилось 
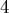


Последнее, что мы ещё не рассмотрели — это как сдвигать прямые в том случае, когда первая окружность не находилась изначально в начале координат. Однако здесь всё просто: из линейности уравнения прямой следует, что от коэффициента 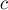

Видео:Внешняя касательная к двум окружностямСкачать
Реализация
Опишем сначала все необходимые структуры данных и другие вспомогательные определения:
Тогда само решение можно записать таким образом (где основная функция для вызова — вторая; а первая функция — вспомогательная):
Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Две окружности на плоскости.
Общие касательные к двум окружностям
 Взаимное расположение двух окружностей Взаимное расположение двух окружностей |
 Общие касательные к двум окружностям Общие касательные к двум окружностям |
 Формулы для длин общих касательных и общей хорды Формулы для длин общих касательных и общей хорды |
 Доказательства формул для длин общих касательных и общей хорды Доказательства формул для длин общих касательных и общей хорды |
Видео:Внутренняя касательная к двум окружностямСкачать

Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  | |
| Каждая из окружностей лежит вне другой |  | |
| Внешнее касание двух окружностей |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  |  |
| Каждая из окружностей лежит вне другой | ||
 | ||
| Внешнее касание двух окружностей | ||
 | ||
| Внутреннее касание двух окружностей | ||
 | ||
| Окружности пересекаются в двух точках | ||
 | ||
 | ||
| Каждая из окружностей лежит вне другой | ||
 Расстояние между центрами окружностей больше суммы их радиусов | ||
| Внешнее касание двух окружностей | ||
 Расстояние между центрами окружностей равно сумме их радиусов | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
 Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой | ||
| Внутренняя касательная к двум окружностям |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  | |
| Внешнее касание двух окружностей |  | |
 | ||
 | ||
| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
 | |
| Внутреннее касание двух окружностей | |
 | |
| Окружности пересекаются в двух точках | |
 | |
| Внешнее касание двух окружностей | |
 | |
 | |
| Каждая из окружностей лежит вне другой | |
 | |
| Внешняя касательная к двум окружностям | |||||||||||||||||||||
| Внутренняя касательная к двум окружностям | |||||||||||||||||||||
| Внутреннее касание двух окружностей | |||||||||||||||||||||
| Окружности пересекаются в двух точках | |||||||||||||||||||||
| Внешнее касание двух окружностей | |||||||||||||||||||||
| Каждая из окружностей лежит вне другой | |||||||||||||||||||||
| Фигура | Рисунок | Формула | ||||||||||||
| Внешняя касательная к двум окружностям |  | |||||||||||||
| Внутренняя касательная к двум окружностям |  | |||||||||||||
| Общая хорда двух пересекающихся окружностей |  | |||||||||||||
| Внешняя касательная к двум окружностям | ||||
 | ||||
| Внутренняя касательная к двум окружностям | ||||
 | ||||
| Общая хорда двух пересекающихся окружностей | ||||
 | ||||
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
 Длина общей хорды двух окружностей вычисляется по формуле Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Касательные к окружностиСкачать  Касательная к окружностиО чем эта статья: Видео:Уравнение касательнойСкачать  Касательная к окружности, секущая и хорда — в чем разницаВ самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу. |





















































